| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 14:27 pon, 9. 11. 2009 Naslov: sigma algebre Postano: 14:27 pon, 9. 11. 2009 Naslov: sigma algebre |
    |
|
|
Ovako, treba mi mala pomoc oko formalnog zapisa, zadataci su mi jasni, no neznam kako bi to trebao formalno zapisati... Pa oko bi netko bio toliko dobar da raspise cijelo rjesenje... Hvala
1. Neka je [latex]\Omega =\left[0,10 \right][/latex]
a)nađite najmanju [latex]\sigma [/latex]-algebru na [latex]\Omega[/latex] koja sadrzi sve skupove [latex]A_{n}=[0,n], n=1,2,3,4,5.[/latex]
b)neka je [latex]B_{n}=[\frac{1}{n},5+\frac {1}{n}], n\in \mathbb{N}[/latex]. Odredite [latex]\limsup B_{n} [/latex]
2. Neka je [latex]\Omega =\{1,2,3,4,5,6\} [/latex] i A,B,C podskupovi od [latex]\Omega[/latex]. Nađite najmanju [latex]\sigma [/latex]-algebru na [latex]\Omega[/latex] koja sadrzi A,B i C ako je [latex]A\bigcup B=\{1,2,4,5\}[/latex], [latex]A=\{2,5\}[/latex], [latex]A\bigcap B=\{2\}[/latex], [latex]C=\{3,6\}[/latex].
Ovako, treba mi mala pomoc oko formalnog zapisa, zadataci su mi jasni, no neznam kako bi to trebao formalno zapisati... Pa oko bi netko bio toliko dobar da raspise cijelo rjesenje... Hvala
1. Neka je 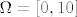
a)nađite najmanju  -algebru na -algebru na 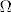 koja sadrzi sve skupove koja sadrzi sve skupove 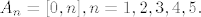
b)neka je 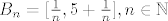 . Odredite . Odredite 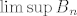
2. Neka je 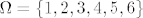 i A,B,C podskupovi od i A,B,C podskupovi od 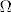 . Nađite najmanju . Nađite najmanju  -algebru na -algebru na 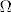 koja sadrzi A,B i C ako je koja sadrzi A,B i C ako je 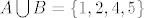 , , 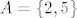 , , 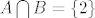 , , 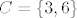 . .
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 10:37 uto, 10. 11. 2009 Naslov: Postano: 10:37 uto, 10. 11. 2009 Naslov: |
    |
|
|
ev ovak, ovaj drugi
A = 2,5
B = 1,2,4
C = 3,6
Daklem, A,B,C moraju bit u sigma algebri
moraju bit i svi njihovi komplementi, znači skupovi {1,3,4,6}, {3,5,6}, {1,2,4,5}. moraleb bit i sve unije unutra, pa onda valda i ovo: {1,2,4,5}, {2,3,5,6}, {1,2,3,4,6}, {1,2,3,4,5,6}, {prazan skup}. sad bi, mislim, trebali biti i komplementi ovih unija, jer, sigma algebra je kao zatvorena na komplementiranje. pab onda trebali bit i ovi: {1,4}, {5}. i eto, mislim da su to svi. sad samo pogledaš sve koje imaš, vidim da sam tu neke prebrojo dvaput, pa onda je ta najmanja sigma algebra svi ti nabrojani skupovi, bez ovih koji se ponavljaju
ovo u prvome pod a:
ovaj vražji omega je kao segment, pa opet, ovdje radiš isto. mora bit unutra A_1 i A_1 komplement i tak dalje, a komplementi ovih čudesa su poluotvoreni intervali <n, 10].
a ovaj limes superior, e to neam pojma šta treba napravit. valda je to ovaj za n = 1, al nekak baš i nisam siguran da to tak ide
ev ovak, ovaj drugi
A = 2,5
B = 1,2,4
C = 3,6
Daklem, A,B,C moraju bit u sigma algebri
moraju bit i svi njihovi komplementi, znači skupovi {1,3,4,6}, {3,5,6}, {1,2,4,5}. moraleb bit i sve unije unutra, pa onda valda i ovo: {1,2,4,5}, {2,3,5,6}, {1,2,3,4,6}, {1,2,3,4,5,6}, {prazan skup}. sad bi, mislim, trebali biti i komplementi ovih unija, jer, sigma algebra je kao zatvorena na komplementiranje. pab onda trebali bit i ovi: {1,4}, {5}. i eto, mislim da su to svi. sad samo pogledaš sve koje imaš, vidim da sam tu neke prebrojo dvaput, pa onda je ta najmanja sigma algebra svi ti nabrojani skupovi, bez ovih koji se ponavljaju
ovo u prvome pod a:
ovaj vražji omega je kao segment, pa opet, ovdje radiš isto. mora bit unutra A_1 i A_1 komplement i tak dalje, a komplementi ovih čudesa su poluotvoreni intervali <n, 10].
a ovaj limes superior, e to neam pojma šta treba napravit. valda je to ovaj za n = 1, al nekak baš i nisam siguran da to tak ide
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Thor
Forumaš(ica)


Pridružen/a: 24. 04. 2009. (10:57:50)
Postovi: (15)16
|
 Postano: 14:07 uto, 10. 11. 2009 Naslov: Postano: 14:07 uto, 10. 11. 2009 Naslov: |
    |
|
|
Nisam ni ja siguran za to ali ovaj pod b) bi možda moglo ić :
Odredis [latex]A_{n}[/latex] niz događaja koji se dobije tako da od C=[0,5] oduzmes [latex]B_{n}[/latex] iz zadatka onda on izgleda nekako ovako
[0,1>,[0,1/2>,[0,1/4>,... i to je padajuci niz događaja pa je njegov lim inf jednak presjek svih [latex]A_{n}[/latex] a to je 0 prazan skup.
Onda imas relaciju [latex]C/\limsup B_{n}=\liminf(C/B_{n})=0[/latex]
pa vrijedi da je C jednak lim sup[latex]B_{n}[/latex] tj riješenje je [0,5]
Sad jel to točno neznam
Nisam ni ja siguran za to ali ovaj pod b) bi možda moglo ić :
Odredis 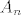 niz događaja koji se dobije tako da od C=[0,5] oduzmes niz događaja koji se dobije tako da od C=[0,5] oduzmes 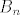 iz zadatka onda on izgleda nekako ovako iz zadatka onda on izgleda nekako ovako
[0,1>,[0,1/2>,[0,1/4>,... i to je padajuci niz događaja pa je njegov lim inf jednak presjek svih 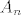 a to je 0 prazan skup. a to je 0 prazan skup.
Onda imas relaciju 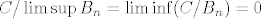
pa vrijedi da je C jednak lim sup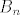 tj riješenje je [0,5] tj riješenje je [0,5]
Sad jel to točno neznam
_________________
Devil's playground
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
Zildyan
Forumaš(ica)

Pridružen/a: 28. 07. 2008. (13:41:39)
Postovi: (20)16
|
 Postano: 21:59 uto, 10. 11. 2009 Naslov: Postano: 21:59 uto, 10. 11. 2009 Naslov: |
    |
|
|
[quote="Milojko"]ev ovak, ovaj drugi
A = 2,5
B = 1,2,4
C = 3,6
Daklem, A,B,C moraju bit u sigma algebri
moraju bit i svi njihovi komplementi, znači skupovi {1,3,4,6}, {3,5,6}, {1,2,4,5}. moraleb bit i sve unije unutra, pa onda valda i ovo: {1,2,4,5}, {2,3,5,6}, {1,2,3,4,6}, {1,2,3,4,5,6}, {prazan skup}. sad bi, mislim, trebali biti i komplementi ovih unija, jer, sigma algebra je kao zatvorena na komplementiranje. pab onda trebali bit i ovi: {1,4}, {5}. i eto, mislim da su to svi. sad samo pogledaš sve koje imaš, vidim da sam tu neke prebrojo dvaput, pa onda je ta najmanja sigma algebra svi ti nabrojani skupovi, bez ovih koji se ponavljaju
[/quote]
sto ne idu i svi oni {nesto}\{nesto}???
| Milojko (napisa): | ev ovak, ovaj drugi
A = 2,5
B = 1,2,4
C = 3,6
Daklem, A,B,C moraju bit u sigma algebri
moraju bit i svi njihovi komplementi, znači skupovi {1,3,4,6}, {3,5,6}, {1,2,4,5}. moraleb bit i sve unije unutra, pa onda valda i ovo: {1,2,4,5}, {2,3,5,6}, {1,2,3,4,6}, {1,2,3,4,5,6}, {prazan skup}. sad bi, mislim, trebali biti i komplementi ovih unija, jer, sigma algebra je kao zatvorena na komplementiranje. pab onda trebali bit i ovi: {1,4}, {5}. i eto, mislim da su to svi. sad samo pogledaš sve koje imaš, vidim da sam tu neke prebrojo dvaput, pa onda je ta najmanja sigma algebra svi ti nabrojani skupovi, bez ovih koji se ponavljaju
|
sto ne idu i svi oni {nesto}\{nesto}???
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
|







