| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
_Neyni_
Forumaš(ica)


Pridružen/a: 17. 02. 2009. (17:31:17)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 15:13 sri, 11. 11. 2009 Naslov: Postano: 15:13 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="_Neyni_"]
14. Neka je V n-dimenzionalni vektorski prostor nad C, n >= 3 i neka je
A E L(V) linearni operator ranga 2, traga 1, a ciji spektar sadrzi broj
-1. Nadite karakteristicni i minimalni polinom operatora A.[/quote]
Ideja je koristiti Jordanov prikaz.
Pa da vidimo što imamo:
-1 je u spektru -> -1 je na dijagonali.
rang matrice je 2 -> ima 2 lin nez stupca -> 2 el na dijagonali !=0 -> 2 svojstvene vrijednosti !=0
trag je 1 -> druga sv vrijednost je 2 (i -1 ne može biti dvostruka)
dakle, imao 3 jordanove klijetke, 2 su dimenzije 1 (za -1 i 2), i jedna je dimenzije n-2 (za nulu). U klijetki za nulu nema jedinica na sporednoj dijagonali, jer bi to povećalo rang.
Sada je lako pročitat karakt i minimalni polinom
| _Neyni_ (napisa): |
14. Neka je V n-dimenzionalni vektorski prostor nad C, n >= 3 i neka je
A E L(V) linearni operator ranga 2, traga 1, a ciji spektar sadrzi broj
-1. Nadite karakteristicni i minimalni polinom operatora A. |
Ideja je koristiti Jordanov prikaz.
Pa da vidimo što imamo:
-1 je u spektru → -1 je na dijagonali.
rang matrice je 2 → ima 2 lin nez stupca → 2 el na dijagonali !=0 → 2 svojstvene vrijednosti !=0
trag je 1 → druga sv vrijednost je 2 (i -1 ne može biti dvostruka)
dakle, imao 3 jordanove klijetke, 2 su dimenzije 1 (za -1 i 2), i jedna je dimenzije n-2 (za nulu). U klijetki za nulu nema jedinica na sporednoj dijagonali, jer bi to povećalo rang.
Sada je lako pročitat karakt i minimalni polinom
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 15:49 sri, 11. 11. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
_Neyni_
Forumaš(ica)


Pridružen/a: 17. 02. 2009. (17:31:17)
Postovi: (1C)16
Spol: 
|
 Postano: 15:47 sri, 11. 11. 2009 Naslov: Postano: 15:47 sri, 11. 11. 2009 Naslov: |
    |
|
|
ok, hvala
:jabuka: :karma:
samo jedna me stvar malo zbunjuje:
[quote="Luuka"]
dakle, imamo 3 jordanove klijetke, 2 su dimenzije 1 (za -1 i 2), i jedna je dimenzije n-2 (za nulu). U klijetki za nulu nema jedinica na sporednoj dijagonali, jer bi to povećalo rang.
[/quote]
kako imamo 3 jordanove klijetke, ako za nulu nema jedinica na sporednoj dijagonali? Zar onda nema n klijetki (ukupno)? :?
ok, hvala
 
samo jedna me stvar malo zbunjuje:
| Luuka (napisa): |
dakle, imamo 3 jordanove klijetke, 2 su dimenzije 1 (za -1 i 2), i jedna je dimenzije n-2 (za nulu). U klijetki za nulu nema jedinica na sporednoj dijagonali, jer bi to povećalo rang.
|
kako imamo 3 jordanove klijetke, ako za nulu nema jedinica na sporednoj dijagonali? Zar onda nema n klijetki (ukupno)? 
_________________
Love one another and you will be happy;
it is as simple and as difficult as that.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Anabelle
Gost
|
 Postano: 17:16 sri, 11. 11. 2009 Naslov: Postano: 17:16 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="behemont"][quote="Saf"][quote="Luuka"][quote="Bug"]
Btw. luuka vidim da si jako aktivan u rjesavanju zadataka na svim podforumima! Nema puno ljudi ko ti! Samo nastavi!
[/quote]
Repetitio est mater studiorum :D[/quote]
AMEN!
Nego, samo da razčistim jednu nedoumicu, funkcionali su operatori sa [latex]V[/latex] u [latex]F[/latex], gdje je [latex]F[/latex] polje, recimo, operator sa [latex]M_3 \rightarrow N[/latex]... Sad jel Rang matrice, odnosno funkcija koja matrici pridružuje broj linearno nezavisnih vektora funkcional?
Jel determinanta funkcional?[/quote]
rang ocito nije funkcional, jer je ogranicen..
a determinanta isto nije jer da je vrijedilo bi det(I)+det(-I)=0
sto nije za parne n..
EDIT: Luka je bio brzi...
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
[quote="Anabelle"]evo da ne otvaram novu temu,moze mi neko pomoci sa zadatkom: neka su A,B iz L(V),dokazite da je AB nilpotentan ako i samo ako je BA nilpotentan[/quote]
Ne znam je li ovo ok, ali probat cemo...
neka je BA nilpotentan indeksa p. tada je (AB)^{p+1}=A(BA)^pB sto je ocito nula...ako nesto ne primjecujem neka netko ispravi..[/quote]
Hvala,ali mislila sam da ne smijemo tako pisati ako ne znamo da A i B komutiraju,nije mi bas jasno..
| behemont (napisa): | | Saf (napisa): | | Luuka (napisa): | | Bug (napisa): |
Btw. luuka vidim da si jako aktivan u rjesavanju zadataka na svim podforumima! Nema puno ljudi ko ti! Samo nastavi!
|
Repetitio est mater studiorum  |
AMEN!
Nego, samo da razčistim jednu nedoumicu, funkcionali su operatori sa 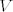 u u 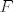 , gdje je , gdje je 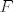 polje, recimo, operator sa polje, recimo, operator sa  ... Sad jel Rang matrice, odnosno funkcija koja matrici pridružuje broj linearno nezavisnih vektora funkcional? ... Sad jel Rang matrice, odnosno funkcija koja matrici pridružuje broj linearno nezavisnih vektora funkcional?
Jel determinanta funkcional? |
rang ocito nije funkcional, jer je ogranicen..
a determinanta isto nije jer da je vrijedilo bi det(I)+det(-I)=0
sto nije za parne n..
EDIT: Luka je bio brzi...
Added after 11 minutes:
| Anabelle (napisa): | | evo da ne otvaram novu temu,moze mi neko pomoci sa zadatkom: neka su A,B iz L(V),dokazite da je AB nilpotentan ako i samo ako je BA nilpotentan |
Ne znam je li ovo ok, ali probat cemo...
neka je BA nilpotentan indeksa p. tada je (AB)^{p+1}=A(BA)^pB sto je ocito nula...ako nesto ne primjecujem neka netko ispravi.. |
Hvala,ali mislila sam da ne smijemo tako pisati ako ne znamo da A i B komutiraju,nije mi bas jasno..
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Anabelle
Gost
|
|
| [Vrh] |
|
zbunjoza
Gost
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
prove22
Forumaš(ica)

Pridružen/a: 11. 02. 2009. (18:57:32)
Postovi: (2F)16
|
|
| [Vrh] |
|
mililimi
Forumaš(ica)
Pridružen/a: 18. 06. 2005. (13:33:48)
Postovi: (6D)16
|
|
| [Vrh] |
|
Maglica
Forumaš(ica)
Pridružen/a: 27. 02. 2009. (16:46:18)
Postovi: (F)16
|
 Postano: 20:55 sri, 11. 11. 2009 Naslov: Postano: 20:55 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="Vip"]Jel u 6. zadatku ima kakve razlike zato jer je operator linearan? Tj. na vježbama smo radili da je A neki operator (nije napomenuto jel linearan) i odredili dal je nilpotentan, indA i Jordanovu formu i na dijagonali su bile nule, dok kasnije kad smo tražili minimalni polinom i Jordanovu formu,imali smo zadano da je linearan i na dijagonali su bile svojstvene vrijednosti.
U mojoj formi u 6.zadatku su nule na dijagonali ali sad nisam sigurna jer me zbunilo ovo linearan operator i operator. :oops: :cry:[/quote]
I mene je baš mučilo to zašto smo negdje odmah stavljali samo nule u Jordanovu formu, a kasnije smo sve raspisivali, ali kad sam raspisala karakteristične polinome za te zadatke s nulama, baš ispadne da je 0 jedina svojstvena vrijednost tako da to stoji.
Nisam baš taj dio bila redovita na vježbama ( :oops: ) tako da to imam kopirano pa neznam ako je bila neka napomena zašto smo to samo odmah ispisali bez računanja
| Vip (napisa): | Jel u 6. zadatku ima kakve razlike zato jer je operator linearan? Tj. na vježbama smo radili da je A neki operator (nije napomenuto jel linearan) i odredili dal je nilpotentan, indA i Jordanovu formu i na dijagonali su bile nule, dok kasnije kad smo tražili minimalni polinom i Jordanovu formu,imali smo zadano da je linearan i na dijagonali su bile svojstvene vrijednosti.
U mojoj formi u 6.zadatku su nule na dijagonali ali sad nisam sigurna jer me zbunilo ovo linearan operator i operator.   |
I mene je baš mučilo to zašto smo negdje odmah stavljali samo nule u Jordanovu formu, a kasnije smo sve raspisivali, ali kad sam raspisala karakteristične polinome za te zadatke s nulama, baš ispadne da je 0 jedina svojstvena vrijednost tako da to stoji.
Nisam baš taj dio bila redovita na vježbama (  ) tako da to imam kopirano pa neznam ako je bila neka napomena zašto smo to samo odmah ispisali bez računanja ) tako da to imam kopirano pa neznam ako je bila neka napomena zašto smo to samo odmah ispisali bez računanja
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:12 sri, 11. 11. 2009 Naslov: Postano: 21:12 sri, 11. 11. 2009 Naslov: |
    |
|
|
Čim za operator postoji matrica koja prikazuje njegovo djelovanje slijedi da je operator linearan (jer su operacije nad matircama takve) :D
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
[quote="prove22"]ako imamo zadan minimalni polinom od A
=x^2 - 4x , treba naći kako izgleda minimalni polinom od A^100[/quote]
Dakle, iz min polinoma od A, mi(x)=x(x-4) čitamo da su 0 i 4 jedine svojstvene vrijednosti, i da su dimenzije najvećeg bloka svake od njih=1. Dakle, prikaz u Jordanovoj formi opretora A je dijagonalna matrica, sa nulama i četvorkama na dijagonali (koliko god puta), i nema jedinica na sporednoj.
A^100 je onda u Jordanovoj bazi matrica sa nulama i 4^100 na dijagonali (i nema jedinica na sporednoj). To znači da je minimalni polimom od A^100
p(x)=x(x-4^100) :D
Čim za operator postoji matrica koja prikazuje njegovo djelovanje slijedi da je operator linearan (jer su operacije nad matircama takve) 
Added after 12 minutes:
| prove22 (napisa): | ako imamo zadan minimalni polinom od A
=x^2 - 4x , treba naći kako izgleda minimalni polinom od A^100 |
Dakle, iz min polinoma od A, mi(x)=x(x-4) čitamo da su 0 i 4 jedine svojstvene vrijednosti, i da su dimenzije najvećeg bloka svake od njih=1. Dakle, prikaz u Jordanovoj formi opretora A je dijagonalna matrica, sa nulama i četvorkama na dijagonali (koliko god puta), i nema jedinica na sporednoj.
A^100 je onda u Jordanovoj bazi matrica sa nulama i 4^100 na dijagonali (i nema jedinica na sporednoj). To znači da je minimalni polimom od A^100
p(x)=x(x-4^100) 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
*Curious
Forumaš(ica)

Pridružen/a: 17. 02. 2008. (15:56:47)
Postovi: (18)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
*Curious
Forumaš(ica)

Pridružen/a: 17. 02. 2008. (15:56:47)
Postovi: (18)16
|
 Postano: 0:57 čet, 12. 11. 2009 Naslov: Postano: 0:57 čet, 12. 11. 2009 Naslov: |
    |
|
|
e, hvala na brzom odg )
može moožda ispravak, u teoretskim pitanjima piše, ako je P(x) minimalni polinom od A, AKKO Q(x)=P(x+lambda) minimalni polinom od A-lambda*I
dakle, mi imamo kod supstitucije t = x-3, pa u konačnici nam je kao ovaj Q(x) = P(t+3)...dakle lambda=3... iz toga bi nam onda slijedilo da je to minimalni polinom od A-3*I???
e, hvala na brzom odg 
može moožda ispravak, u teoretskim pitanjima piše, ako je P(x) minimalni polinom od A, AKKO Q(x)=P(x+lambda) minimalni polinom od A-lambda*I
dakle, mi imamo kod supstitucije t = x-3, pa u konačnici nam je kao ovaj Q(x) = P(t+3)...dakle lambda=3... iz toga bi nam onda slijedilo da je to minimalni polinom od A-3*I???
|
|
| [Vrh] |
|
mililimi
Forumaš(ica)
Pridružen/a: 18. 06. 2005. (13:33:48)
Postovi: (6D)16
|
|
| [Vrh] |
|
AnaP
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (15:41:46)
Postovi: (153)16
|
|
| [Vrh] |
|
|














