| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 18:01 sri, 11. 11. 2009 Naslov: Postano: 18:01 sri, 11. 11. 2009 Naslov: |
    |
|
|
L = {p element P_4 : p(2) = 0} i M = {p element P_4 : p(3) =0}.
ti polinomi zgledaju ovak: ax^4+bx^3+cx^2+dx+e.
Sad uvrstiš svoj uvjet (napisat ću za L) i imaš
16a+8b+4c+2d+e=0 iz toga izgaziš e:
e=-16a-8b-4c-2d
Sad imamo polinom oblika:
ax^4+bx^3+cx^2+dx+(-16a-8b-4c-2d)
sad baza:
(x^4,0,0,0,-16),(0,x^3,0,0,-8),(0,0,x^2,0,-4),(0,0,0,x,-2).
Na potpuno isti način se nađe baza za M
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
Ako se ne varam baza za M je:
(x^4,0,0,0,-81),(0,x^3,0,0,-27),(0,0,x^2,0,-9),(0,0,0,x,-3)
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
Sad se vektori koji su baza za L i oni koji su baza za M uguraju u isti skup i provjerava se nezavisnost, te se dobije da su vektori
(x^4,0,0,0,-16),(0,x^3,0,0,-8),(0,0,x^2,0,-4),(0,0,0,x,-2),(x^4,0,0,0,-81)
međusobno nezavisni, te su oni baza za M+L
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
Sad vidimo da je dimM+L=5, a znamo da je dimM=dimL=4, pa je dim(MpresjekL)=3
L = {p element P_4 : p(2) = 0} i M = {p element P_4 : p(3) =0}.
ti polinomi zgledaju ovak: ax^4+bx^3+cx^2+dx+e.
Sad uvrstiš svoj uvjet (napisat ću za L) i imaš
16a+8b+4c+2d+e=0 iz toga izgaziš e:
e=-16a-8b-4c-2d
Sad imamo polinom oblika:
ax^4+bx^3+cx^2+dx+(-16a-8b-4c-2d)
sad baza:
(x^4,0,0,0,-16),(0,x^3,0,0,-8),(0,0,x^2,0,-4),(0,0,0,x,-2).
Na potpuno isti način se nađe baza za M
Added after 2 minutes:
Ako se ne varam baza za M je:
(x^4,0,0,0,-81),(0,x^3,0,0,-27),(0,0,x^2,0,-9),(0,0,0,x,-3)
Added after 5 minutes:
Sad se vektori koji su baza za L i oni koji su baza za M uguraju u isti skup i provjerava se nezavisnost, te se dobije da su vektori
(x^4,0,0,0,-16),(0,x^3,0,0,-8),(0,0,x^2,0,-4),(0,0,0,x,-2),(x^4,0,0,0,-81)
međusobno nezavisni, te su oni baza za M+L
Added after 2 minutes:
Sad vidimo da je dimM+L=5, a znamo da je dimM=dimL=4, pa je dim(MpresjekL)=3
Zadnja promjena: eve; 18:02 sri, 11. 11. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
GoranV
Forumaš(ica)

Pridružen/a: 20. 11. 2008. (11:22:01)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:46 sri, 11. 11. 2009 Naslov: Postano: 19:46 sri, 11. 11. 2009 Naslov: |
    |
|
|
Ok, hvala, sad naravno slijedi pitanje je li taj prostor u M potprostor od C? Riješio sam, ali nisam siguran, pa eto, za provjeru.
Ok, hvala, sad naravno slijedi pitanje je li taj prostor u M potprostor od C? Riješio sam, ali nisam siguran, pa eto, za provjeru.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Talija
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (17:01:00)
Postovi: (4)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
 Postano: 22:00 sri, 11. 11. 2009 Naslov: Postano: 22:00 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="eve"]
Sad se vektori koji su baza za L i oni koji su baza za M uguraju u isti skup i provjerava se nezavisnost, te se dobije da su vektori
(x^4,0,0,0,-16),(0,x^3,0,0,-8),(0,0,x^2,0,-4),(0,0,0,x,-2),(x^4,0,0,0,-81)
međusobno nezavisni, te su oni baza za M+L
[/quote]
kako si vidila da su oni nezavisni???
| eve (napisa): |
Sad se vektori koji su baza za L i oni koji su baza za M uguraju u isti skup i provjerava se nezavisnost, te se dobije da su vektori
(x^4,0,0,0,-16),(0,x^3,0,0,- ,(0,0,x^2,0,-4),(0,0,0,x,-2),(x^4,0,0,0,-81) ,(0,0,x^2,0,-4),(0,0,0,x,-2),(x^4,0,0,0,-81)
međusobno nezavisni, te su oni baza za M+L
|
kako si vidila da su oni nezavisni???
_________________
Give me a place to stand, and I will move the earth.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 22:07 sri, 11. 11. 2009 Naslov: Postano: 22:07 sri, 11. 11. 2009 Naslov: |
    |
|
|
tako da pomnožiš prva 4 sa skalarima i gledaš da li možeš dobit petog.. znači:
(Ax^4,0,0,0,-16A)+(0,Bx^3,0,0,-8B)+(0,0,Cx^2,0,-4C)+(0,0,0,Dx,-2D)=(x^4,0,0,0,-81)
sad gledaš šta sve sa lijeve strane imaš uz x^4 a šta sa desne:
A=1,
isto i za ostale komponente:
B=0
C=0
-16A-8B-4C-2D=-18, uvrstiš brojeve koje imaš za A,B,C,D i dobiješ
-16=-81 što je kontradikcija, pa su oni nezavisni
tako da pomnožiš prva 4 sa skalarima i gledaš da li možeš dobit petog.. znači:
(Ax^4,0,0,0,-16A)+(0,Bx^3,0,0,-8B)+(0,0,Cx^2,0,-4C)+(0,0,0,Dx,-2D)=(x^4,0,0,0,-81)
sad gledaš šta sve sa lijeve strane imaš uz x^4 a šta sa desne:
A=1,
isto i za ostale komponente:
B=0
C=0
-16A-8B-4C-2D=-18, uvrstiš brojeve koje imaš za A,B,C,D i dobiješ
-16=-81 što je kontradikcija, pa su oni nezavisni
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:28 sri, 11. 11. 2009 Naslov: Postano: 23:28 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="ajaxcy"]hmmm...pomoc oko drugog dijela? :D[/quote]
Neka je [latex]x \in M[/latex] proizvoljan vektor.
Zbog toga što je skup [latex]\{a_1, a_2, ... , a_k\}[/latex] sustav izvodnica za [latex]M[/latex], slijedi da se [latex]x[/latex] može prikazati kao njihova linearna kombinacija.
Kako su po (a) ti isti vektori [latex]a_1, a_2, ... , a_k \in L[/latex] i [latex]L \leqslant V[/latex] (potprostor je zatvoren na linearne kombinacije svojih elemenata), zaključujemo da je [latex]x \in L[/latex].
Analogno se dokazuje obrnuta inkluzija.
| ajaxcy (napisa): | hmmm...pomoc oko drugog dijela?  |
Neka je  proizvoljan vektor. proizvoljan vektor.
Zbog toga što je skup 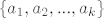 sustav izvodnica za sustav izvodnica za  , slijedi da se , slijedi da se  može prikazati kao njihova linearna kombinacija. može prikazati kao njihova linearna kombinacija.
Kako su po (a) ti isti vektori 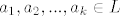 i i 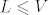 (potprostor je zatvoren na linearne kombinacije svojih elemenata), zaključujemo da je (potprostor je zatvoren na linearne kombinacije svojih elemenata), zaključujemo da je 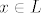 . .
Analogno se dokazuje obrnuta inkluzija.
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
|





















