|
[quote="ajaxcy"][quote="Gino"]prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
z_1&&&+&z_3&-&iz_4&=&0
\end{array}[/latex]
oduzimanjem dobis
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
&-&iz_2&+&z_3&+&(1-i)z_4&=&0
\end{array}[/latex]
stavis da su [latex]z_2[/latex] i [latex]z_4 [/latex]parametri pa imas
[latex]z_1=-it+s\\
z_2=t\\
z_3=it-(1-i)s\\
z_4=s[/latex]
dakle [latex]z=\left( z_1,z_2,z_3,z_4\right)=\left( -it+s, t, it-(1-i)s,s \right)=t\left( -i,1,i,0\right) +s\left( 1,0,i-1,1\right)[/latex]
pa je baza za [latex]M[/latex] skup [latex]\left\{ \left( -i,1,i,0\right) ,\left( 1,0,i-1,1\right)\right\}[/latex]
treci dio takoder necu pisat....[/quote]
sve je ovo okej i rjesila sam do tud:
baza za [latex]M[/latex] skup [latex]\left\{ \left( -i,1,i,0\right) ,\left( 1,0,i-1,1\right)\right\}[/latex]
ali ne kuzim ako smo vec u C zasto onda baza nije (1,0,-1,1)(0,0,i,0)(0,1,0,0)(-i,0,i,0)?????[/quote]
:?:
pa to nije isto, ti hoces rec da je vektor (0,1,0,0) iz M, primjeti da nije ispunjena prva jednakost koja se trazi da bi vektor bio iz M (drugu nisam gledao... mozda ne ispunjava ni nju)
neovisno o tome dal si nad C, ili nad R, ne "razdvajas bazu" za M, vec samo vidis sto ces dodati, tesko mi je to ovako objasnit al nadam se da je jasno
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
ako ti nije jasno, dodi na demonstrature ili odi na konzultacije, jer je podosta bitno da ti to bude jasno, za daljnije svladavanje gradiva, neovisno o kolokviju...
uglavnom, sretno vam na kolokviju :D
| ajaxcy (napisa): | | Gino (napisa): | prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
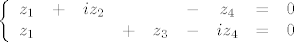
oduzimanjem dobis
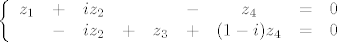
stavis da su 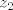 i i 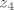 parametri pa imas parametri pa imas
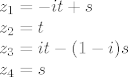
dakle 
pa je baza za  skup skup 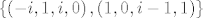
treci dio takoder necu pisat.... |
sve je ovo okej i rjesila sam do tud:
baza za  skup skup 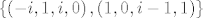
ali ne kuzim ako smo vec u C zasto onda baza nije (1,0,-1,1)(0,0,i,0)(0,1,0,0)(-i,0,i,0)????? |

pa to nije isto, ti hoces rec da je vektor (0,1,0,0) iz M, primjeti da nije ispunjena prva jednakost koja se trazi da bi vektor bio iz M (drugu nisam gledao... mozda ne ispunjava ni nju)
neovisno o tome dal si nad C, ili nad R, ne "razdvajas bazu" za M, vec samo vidis sto ces dodati, tesko mi je to ovako objasnit al nadam se da je jasno
Added after 6 minutes:
ako ti nije jasno, dodi na demonstrature ili odi na konzultacije, jer je podosta bitno da ti to bude jasno, za daljnije svladavanje gradiva, neovisno o kolokviju...
uglavnom, sretno vam na kolokviju 
_________________
Mario Berljafa
|




