| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kyra29
Forumaš(ica)

Pridružen/a: 16. 02. 2009. (17:23:47)
Postovi: (3F)16
Spol: 
|
|
| [Vrh] |
|
mery
Forumaš(ica)

Pridružen/a: 01. 12. 2008. (21:57:21)
Postovi: (43)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
anchi
Gost
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 14:56 pon, 9. 11. 2009 Naslov: Postano: 14:56 pon, 9. 11. 2009 Naslov: |
    |
|
|
ajme, koja pušiona
ajme, koja pušiona
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
(s)Venn
Forumaš(ica)

Pridružen/a: 18. 02. 2009. (17:59:25)
Postovi: (40)16
Lokacija: Velika Gorica
|
 Postano: 16:28 pon, 9. 11. 2009 Naslov: Postano: 16:28 pon, 9. 11. 2009 Naslov: |
    |
|
|
[quote="anchi"]jel moze ko napisati tocan dan i vrijeme zalbi??hvala[/quote]
I ja bih molio isto. Zahvaljujem unaprijed... :wink:
| anchi (napisa): | | jel moze ko napisati tocan dan i vrijeme zalbi??hvala |
I ja bih molio isto. Zahvaljujem unaprijed... 
_________________ ..pišem pjesme, sviram bluz, radost i tugu na stihove lomim.. |
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
 Postano: 17:25 pon, 9. 11. 2009 Naslov: Postano: 17:25 pon, 9. 11. 2009 Naslov: |
    |
|
|
može li netko od kolega koji su prošle godine slušali difraf ili netko od asistenata napisati kako se bodovi sa kolokvija pretvaraju u konačne bodove.
npr, konačno svaki kolokvij i završni ispit nosi po 30 boda (pa uz bliceve 10+30+30+30=100)
ali jedan kolokvij nema 30, nego 120 bodova! znači li to da za 15 "konačnih bodova" treba osvojiti 60 "kolokvijskih bodova"?
ali to nije sve, jer na prijašnjim kolokvijima (nisam siguran je li tako i ove godine, nisam gledao) piše da je za maksimum bodova na kolokvijima dovoljno ostvariti 100 bodova. to valjda znači da 100 "kolokvijskih bodova" odgovara 30 "konačnih bodova" :?:
odnosno, za 15 "konačnih bodova" treba imati 50 "kolokvijskih bodova", a ne 60?
kako je to bilo prošle godine? :?
može li netko od kolega koji su prošle godine slušali difraf ili netko od asistenata napisati kako se bodovi sa kolokvija pretvaraju u konačne bodove.
npr, konačno svaki kolokvij i završni ispit nosi po 30 boda (pa uz bliceve 10+30+30+30=100)
ali jedan kolokvij nema 30, nego 120 bodova! znači li to da za 15 "konačnih bodova" treba osvojiti 60 "kolokvijskih bodova"?
ali to nije sve, jer na prijašnjim kolokvijima (nisam siguran je li tako i ove godine, nisam gledao) piše da je za maksimum bodova na kolokvijima dovoljno ostvariti 100 bodova. to valjda znači da 100 "kolokvijskih bodova" odgovara 30 "konačnih bodova" 
odnosno, za 15 "konačnih bodova" treba imati 50 "kolokvijskih bodova", a ne 60?
kako je to bilo prošle godine? 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
 Postano: 19:09 pon, 9. 11. 2009 Naslov: Postano: 19:09 pon, 9. 11. 2009 Naslov: |
    |
|
|
Prošle godine je bilo da je jedan bod s kolokvija nosio 0,3 pravih bodova.
Dakle, ako si na kolokvijima imao 100 bodova dobio si 30 pravih, ako si primjerice imao 110 bodova, dobio si 33 boda.
Također iako su blicevi nosili 10 bodova, ako si ostvario više od 10 bodova, svi su ti se bodovi pribrajali u konačnu cifru...
Prošle godine je bilo da je jedan bod s kolokvija nosio 0,3 pravih bodova.
Dakle, ako si na kolokvijima imao 100 bodova dobio si 30 pravih, ako si primjerice imao 110 bodova, dobio si 33 boda.
Također iako su blicevi nosili 10 bodova, ako si ostvario više od 10 bodova, svi su ti se bodovi pribrajali u konačnu cifru...
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:39 uto, 10. 11. 2009 Naslov: Postano: 0:39 uto, 10. 11. 2009 Naslov: |
    |
|
|
Koliko sam ja shvatio, bodovi s kolokvija će se zbrojiti (s prvog i drugog) i biti pomnoženi s [latex]\frac{3}{10}[/latex], pa je to sveukupni broj bodova. 12 je dodatnih, a 60 "regularnih"...
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
Za žalbe (opet, koliko sam ja skužio), termini su kad i [url=http://web.math.hr/nastava/difraf/termini_dir.html]termini konzultacija[/url] profesora.
I opet, koliko sam skužio :D, profesorima se možete javiti i na mail, koji je u obliku ime.prezime@math.hr
Koliko sam ja shvatio, bodovi s kolokvija će se zbrojiti (s prvog i drugog) i biti pomnoženi s 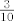 , pa je to sveukupni broj bodova. 12 je dodatnih, a 60 "regularnih"... , pa je to sveukupni broj bodova. 12 je dodatnih, a 60 "regularnih"...
Added after 2 minutes:
Za žalbe (opet, koliko sam ja skužio), termini su kad i termini konzultacija profesora.
I opet, koliko sam skužio  , profesorima se možete javiti i na mail, koji je u obliku ime.prezime@math.hr , profesorima se možete javiti i na mail, koji je u obliku ime.prezime@math.hr
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:29 pet, 13. 11. 2009 Naslov: Postano: 21:29 pet, 13. 11. 2009 Naslov: |
    |
|
|
Pretpostavimo najprije da [latex]a_i^k \to 0,\ \forall i =1,\, 2,\, \ldots,\, n[/latex], tada [latex]\forall \varepsilon > 0[/latex], [latex]\forall i = 1,\, 2,\, \ldots,\, n[/latex], [latex]\exists k_i \in \mathbb{N}[/latex], takav da je [latex]\forall k \in \mathbb{N},\, k \geq k_i[/latex], [latex]\left|a_i^k\right| < \frac{\sqrt{\varepsilon}}{\sqrt{n}}[/latex]. Uzmemo [latex]k_0 = \max{k_i}[/latex], tada je očito [latex]\forall k \in \mqthbb{N}[/latex], [latex]k \geq k_0[/latex], [latex]\sum_{i=1}^{n}{\left|a_i^k\right|^2} < \varepsilon[/latex].
U drugom smjeru, pretpostavimo surpotno, najprije da za neki [latex]i[/latex], [latex]a_i^k[/latex] divergira, to je očito nemoguće, jer se sumiraju nenegativni brojevi, pa to može divergirati jedino u [latex]+\infty[/latex], a onda očito suma ne konvergira. Sada pretpostavimo da neki [latex]a_i^k[/latex] konvergira u nešto različito od nule, tada opet lako vidimo da cijela suma nikako ne može konvergirati u nulu (zato jer sumiramo nenegativne brojeve!), kontradikcija. Dakle, svaki [latex]a_i^k[/latex] konvergira u nulu, a time i niz njegovih apsolutnih vrijednosti ide u nulu, a time i niz kvadrata njegovih apsolutnih vrijednosti.
Pretpostavimo najprije da 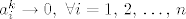 , tada , tada 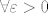 , , 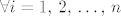 , , 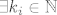 , takav da je , takav da je 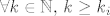 , , 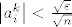 . Uzmemo . Uzmemo 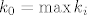 , tada je očito , tada je očito 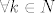 , ,  , , 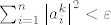 . .
U drugom smjeru, pretpostavimo surpotno, najprije da za neki  , , 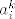 divergira, to je očito nemoguće, jer se sumiraju nenegativni brojevi, pa to može divergirati jedino u divergira, to je očito nemoguće, jer se sumiraju nenegativni brojevi, pa to može divergirati jedino u  , a onda očito suma ne konvergira. Sada pretpostavimo da neki , a onda očito suma ne konvergira. Sada pretpostavimo da neki 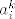 konvergira u nešto različito od nule, tada opet lako vidimo da cijela suma nikako ne može konvergirati u nulu (zato jer sumiramo nenegativne brojeve!), kontradikcija. Dakle, svaki konvergira u nešto različito od nule, tada opet lako vidimo da cijela suma nikako ne može konvergirati u nulu (zato jer sumiramo nenegativne brojeve!), kontradikcija. Dakle, svaki 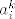 konvergira u nulu, a time i niz njegovih apsolutnih vrijednosti ide u nulu, a time i niz kvadrata njegovih apsolutnih vrijednosti. konvergira u nulu, a time i niz njegovih apsolutnih vrijednosti ide u nulu, a time i niz kvadrata njegovih apsolutnih vrijednosti.
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 16:41 sub, 14. 11. 2009 Naslov: Postano: 16:41 sub, 14. 11. 2009 Naslov: |
    |
|
|
Ja sam imao ovaj iz druge grupe
prvi smjer, neka ova suma a_i-ova teži u nulu. primjetim da je to zapravo 1-norma od a^k, k iz N. Zbog ekvivalencija normi mi slijedi da i u normi beskonačno to teži u nulu, pa mi definicija norme beskonačno povlači da svaki a^k_i teži u nulu.
analogan dokaz bi prošao i za ovaj drugi zadatak, bar mislim
onaj drugi smjer je analogan jankrijevom, sam što je sve bez korijena
Ja sam imao ovaj iz druge grupe
prvi smjer, neka ova suma a_i-ova teži u nulu. primjetim da je to zapravo 1-norma od a^k, k iz N. Zbog ekvivalencija normi mi slijedi da i u normi beskonačno to teži u nulu, pa mi definicija norme beskonačno povlači da svaki a^k_i teži u nulu.
analogan dokaz bi prošao i za ovaj drugi zadatak, bar mislim
onaj drugi smjer je analogan jankrijevom, sam što je sve bez korijena
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
|

















