| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 23:25 uto, 8. 12. 2009 Naslov: Postano: 23:25 uto, 8. 12. 2009 Naslov: |
    |
|
|
Ovo je trokutasta matrica, i vidi iz aviona se vide svojstvene vrijednosti... daj si pročitaj malo predavanja i ostalo... ne znam kak ćeš ovo ako provjera linearnog operatora nije jasna...
Ovo je trokutasta matrica, i vidi iz aviona se vide svojstvene vrijednosti... daj si pročitaj malo predavanja i ostalo... ne znam kak ćeš ovo ako provjera linearnog operatora nije jasna...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 1:31 sri, 9. 12. 2009 Naslov: Postano: 1:31 sri, 9. 12. 2009 Naslov: |
    |
|
|
Ako imas
[latex]a \cdot b \cdot c \cdot d = 0[/latex],
onda je valjda jasno da mora biti
[latex]a = 0[/latex] ili [latex]b = 0[/latex] ili [latex]c = 0[/latex] ili [latex]d = 0[/latex].
E, a ti umjesto
[latex]a \cdot b \cdot c \cdot d = 0[/latex],
imas
[latex](\lambda - 1)(\lambda - 3)(\lambda - 5)(\lambda - 6) = 0[/latex]
Sad jasnije?
Ako imas
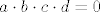 , ,
onda je valjda jasno da mora biti
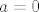 ili ili 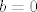 ili ili  ili ili 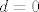 . .
E, a ti umjesto
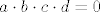 , ,
imas
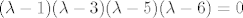
Sad jasnije?
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
 Postano: 15:00 sri, 9. 12. 2009 Naslov: Postano: 15:00 sri, 9. 12. 2009 Naslov: |
    |
|
|
Onda bi treba kao svaku nultočku izjednači s nulom
te ispada da je lamda_1 - 1= 0 => lamda_1 =1
lamda_2 = 3
lamda_3 = 5
lamda_4= 6
Ne, ne bi trebalo biti tako...
Trabam izraziti lamde, koje će mi završitit s potencijama, te kad se to sredi dobijem sređene lamde u zagradama i tamo mi ispadnu nultočke....
Npr. imam matricu A={0 5 8;5 0 8;8 5 0} koja je slična mojoj, ali opet drugačija. Kod nje se računa kark. polinom i to tako:
k(lamda)=det(lamda* I-A) = (lamde dođu na dijagonala, a ostali brojevi promijene predznaki to je = lamda^3 - 129 lamda - 520
iz toga su nultočke lamda1=-8, l2= -5, l3=13
E sad , to treb aprimijenit kod mog slučaja.. veća je matrica i k tome trokutasta...
Onda bi treba kao svaku nultočku izjednači s nulom
te ispada da je lamda_1 - 1= 0 => lamda_1 =1
lamda_2 = 3
lamda_3 = 5
lamda_4= 6
Ne, ne bi trebalo biti tako...
Trabam izraziti lamde, koje će mi završitit s potencijama, te kad se to sredi dobijem sređene lamde u zagradama i tamo mi ispadnu nultočke....
Npr. imam matricu A={0 5 8;5 0 8;8 5 0} koja je slična mojoj, ali opet drugačija. Kod nje se računa kark. polinom i to tako:
k(lamda)=det(lamda* I-A) = (lamde dođu na dijagonala, a ostali brojevi promijene predznaki to je = lamda^3 - 129 lamda - 520
iz toga su nultočke lamda1=-8, l2= -5, l3=13
E sad , to treb aprimijenit kod mog slučaja.. veća je matrica i k tome trokutasta...
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Gogs
Forumaš(ica)


Pridružen/a: 17. 10. 2002. (22:28:12)
Postovi: (155)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:26 pet, 11. 12. 2009 Naslov: Postano: 16:26 pet, 11. 12. 2009 Naslov: |
    |
|
|
Sve ti je već gore napisano, samo to treba znat pročitat... ko što sam reko, puuuuno ti rupa imaš, iz najjednostavnijih osnova, tako da ti forum ne može pomoć, samo instrukcije ili demonstature, di će ti netko to moć objasnit
Sve ti je već gore napisano, samo to treba znat pročitat... ko što sam reko, puuuuno ti rupa imaš, iz najjednostavnijih osnova, tako da ti forum ne može pomoć, samo instrukcije ili demonstature, di će ti netko to moć objasnit
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
 Postano: 17:20 pet, 11. 12. 2009 Naslov: Postano: 17:20 pet, 11. 12. 2009 Naslov: |
    |
|
|
Da, imam sve ispisano...
MOje pretpostavke, od kojih mi ni jednu nije nitko ni potvrdio,a niti opovrguo, te odgovore forumaša , svatko svoj i kako da onda znam gdje je ključan dio rješenja moga problema zadatka...
Lamde, rješenja su
1, 3, 5 i 6? ili su to nultočke polinoma?
Da, imam sve ispisano...
MOje pretpostavke, od kojih mi ni jednu nije nitko ni potvrdio,a niti opovrguo, te odgovore forumaša , svatko svoj i kako da onda znam gdje je ključan dio rješenja moga problema zadatka...
Lamde, rješenja su
1, 3, 5 i 6? ili su to nultočke polinoma?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:24 pet, 11. 12. 2009 Naslov: Postano: 17:24 pet, 11. 12. 2009 Naslov: |
    |
|
|
[quote="tomi365"]
Lamde, rješenja su
1, 3, 5 i 6? ili su to nultočke polinoma?[/quote]
Po ovome se vidi na nemaš pojma o čemu pričaš, da ti je sve nejasno :D
Evo još samo da ti ovo odgovorim:
Svaka svojstvena vrijednost matrice je nultočka karakterističnog polinoma i tako ju računamo. Dakle, da, tvoje svojstvene vrijednosti su 1,3,5,6 jer su nultočke karakterističnog polinoma.
| tomi365 (napisa): |
Lamde, rješenja su
1, 3, 5 i 6? ili su to nultočke polinoma? |
Po ovome se vidi na nemaš pojma o čemu pričaš, da ti je sve nejasno 
Evo još samo da ti ovo odgovorim:
Svaka svojstvena vrijednost matrice je nultočka karakterističnog polinoma i tako ju računamo. Dakle, da, tvoje svojstvene vrijednosti su 1,3,5,6 jer su nultočke karakterističnog polinoma.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
 Postano: 18:16 pet, 11. 12. 2009 Naslov: Postano: 18:16 pet, 11. 12. 2009 Naslov: |
    |
|
|
Ok, lamde = nultočke k. polinoma = svojstvene vrij. matrice
To sad stoji...
[size=9][color=#999999]Added after 32 minutes:[/color][/size]
Sad još samo nek sjedne potprostor te mat. i B^-1 pomoću potencija B mat.
ok, kužim b^-1, al pomoć potencija b mat, to ne kužim...
nemam potencije, tj. ja ih ne vidim...
Ok, lamde = nultočke k. polinoma = svojstvene vrij. matrice
To sad stoji...
Added after 32 minutes:
Sad još samo nek sjedne potprostor te mat. i B^-1 pomoću potencija B mat.
ok, kužim b^-1, al pomoć potencija b mat, to ne kužim...
nemam potencije, tj. ja ih ne vidim...
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:11 pet, 11. 12. 2009 Naslov: Postano: 20:11 pet, 11. 12. 2009 Naslov: |
    |
|
|
Ovako, iz Hamilton-Cayleyevog tm slijedi da matrica poništava svoj karakteristični polinom, tj da je k(A)=0.
Dakle, samo raspiši onaj svoj polinom di je lambda, umjesto lambda uvrsti A, prebaci ono di je I na jednu stranu, ostalo na drugu i onda pomnoži sa A^-1. I eto polinoma u A koji daje A^-1 :D
A sv potprostore ti neću tu objašnjavat, predug bi to bio post :D
Ovako, iz Hamilton-Cayleyevog tm slijedi da matrica poništava svoj karakteristični polinom, tj da je k(A)=0.
Dakle, samo raspiši onaj svoj polinom di je lambda, umjesto lambda uvrsti A, prebaci ono di je I na jednu stranu, ostalo na drugu i onda pomnoži sa A^-1. I eto polinoma u A koji daje A^-1 
A sv potprostore ti neću tu objašnjavat, predug bi to bio post 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
 Postano: 21:44 pet, 11. 12. 2009 Naslov: Postano: 21:44 pet, 11. 12. 2009 Naslov: |
    |
|
|
Dobar vic, nema šta :D
Da li koristim pritom onaj umnožak koji sam prije izračunao (l-1)(l-3),...
a iznosi lamda^4 ,... te tamo zamijenim lamde u A - (koji A?) kao što si rekao te
izračunam...
Primio sam se potprostora, i ima ih veelikih 4 slučaja
za lamdu 1, 3, 5, 6
te sam krenuo od
A-I=
te idem
A-3I=
A-5I=
A-6I=
da svedem matricu onim nekim pravilima na 1 ili 2 retka pa dobijem x-eve 1 i 2 te
da dobijem dim S(1)=1
a što se tiće B^-1, može se riješiti na 2 načina koja poznam,
a zovu se - pomoću min.polinoma i bez direktnog invertiranja...
Pa koji je ovaj pomoću potenc. ?
Dobar vic, nema šta 
Da li koristim pritom onaj umnožak koji sam prije izračunao (l-1)(l-3),...
a iznosi lamda^4 ,... te tamo zamijenim lamde u A - (koji A?) kao što si rekao te
izračunam...
Primio sam se potprostora, i ima ih veelikih 4 slučaja
za lamdu 1, 3, 5, 6
te sam krenuo od
A-I=
te idem
A-3I=
A-5I=
A-6I=
da svedem matricu onim nekim pravilima na 1 ili 2 retka pa dobijem x-eve 1 i 2 te
da dobijem dim S(1)=1
a što se tiće B^-1, može se riješiti na 2 načina koja poznam,
a zovu se - pomoću min.polinoma i bez direktnog invertiranja...
Pa koji je ovaj pomoću potenc. ?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:32 pet, 11. 12. 2009 Naslov: Postano: 22:32 pet, 11. 12. 2009 Naslov: |
    |
|
|
Za ovu matricu je minimalni polinom jednak karakterističnom ;)
A ovako nekako se ide, pisat ću primjer bezveze, ne da mi se isčitavat točni koeficijenti. Neka je k(x) karakteristični polinom od A:
[latex]k(x)=x^4+3x^3-17x^2-5x + 9[/latex]
Hamilton-Cayleyev tm kaže da matrica poništava svoj karakt polinom, dakle
[latex]k(A)=0[/latex], tj
[latex]A^4+3A^3-17A^2-5A + 9I = 0[/latex]
iz toga slijedi da je
[latex]-\frac{1}{9}A^4-\frac{1}{3}A^3+\frac{17}{9}A^2+\frac{5}{9}A = I[/latex] , pa množenjem sa A^-1 dobivamo:
[latex]-\frac{1}{9}A^3-\frac{1}{3}A^2+\frac{17}{9}A+\frac{5}{9}I = A^{-1}[/latex]
Isti je postupak iz minimalnog polinoma.
Za ovu matricu je minimalni polinom jednak karakterističnom 
A ovako nekako se ide, pisat ću primjer bezveze, ne da mi se isčitavat točni koeficijenti. Neka je k(x) karakteristični polinom od A:
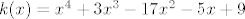
Hamilton-Cayleyev tm kaže da matrica poništava svoj karakt polinom, dakle
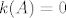 , tj , tj
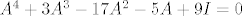
iz toga slijedi da je
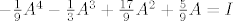 , pa množenjem sa A^-1 dobivamo: , pa množenjem sa A^-1 dobivamo:
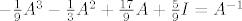
Isti je postupak iz minimalnog polinoma.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|












