| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:29 sub, 19. 12. 2009 Naslov: Postano: 14:29 sub, 19. 12. 2009 Naslov: |
    |
|
|
Zadatak nije težak, makar zbilja pretjerava s indukcijom :D, a budući da smo ga (ili neki iz drugih grupa, a svi su isti) na demonstraturama više puta pokazivali, a pretpostavljam da isto vrijedi i za ostale demonstratore, a i sigurno se tako nešto (ako ne i doslovno ovaj zadatak) radilo na vježbama, možda je sad korisnije da samo neke osnovne korake i zaključke, a onda je na tebi da popuniš rupe i pitaš ako nešto nije jasno :).
Dakle, prvo ćemo "odrediti limes", tj. pretpostavimo da limes postoji i da iznosi [latex]L[/latex]. Onda za njega vrijedi [latex]\displaystyle L=\frac{L^2}{4}+\frac{1}{3}[/latex]. To je kvadratna jednadžba kojoj su korijeni [latex]\displaystyle \frac{6-2\sqrt{6}}{3}[/latex] i [latex]\displaystyle \frac{6+2\sqrt{6}}{3}[/latex].
Dokazat ćemo da su svi članovi niza manji od manjeg kandidata za limes, kao i da je niz rastuć. Tada će iz ograničenosti i monotonosti slijediti da je niz konvergentan, a limes će mu biti manji kandidat (da je limes veći kandidat, morali bismo imati članove proizvoljno blizu njemu, a to je nemoguće jer ćemo dokazati da su svi članovi niza manji od manjeg kandidata).
Sad hoćemo dokazati [latex]\displaystyle a_n\leq\frac{6-2\sqrt{6}}{3}[/latex]. Ta tvrdnja očito vrijedi za [latex]n=1[/latex] i [latex]n=2[/latex], a dalje nastavljamo jakom indukcijom, tj. pretpostavljamo da tvrdnja vrijedi za [latex]1, 2, \ldots, n-1, n[/latex] ([latex]n\geq 2[/latex]).
(Uzgred, tu implicitno koristimo i da je [latex]a_n\geq 0[/latex] za svaki prirodni [latex]n[/latex], a to je dosta očito da vrijedi, a može se formalno dokazati i indukcijom.)
Znamo da je sada [latex]\displaystyle a_{n+1}=\frac{a_na_{n-1}}{4}+\frac{1}{3}\leq\frac{1}{4}(\frac{6-2\sqrt{6}}{3})^2+\frac{1}{3}[/latex], a kad se to raspiše, dobivamo upravo traženi korak indukcije.
Još preostaje pokazati monotonost, tj. da je [latex]a_n\leq a_{n+1}[/latex] za svaki prirodni [latex]n[/latex]. Tvrdnja vrijedi za [latex]n=1[/latex] (i, možda nam zatreba, za [latex]n=2[/latex], to lako fizički provjerimo). Sad opet idemo jakom indukcijom i pretpostavljamo [latex]a_1\leq a_2\leq \ldots\leq a_{n-2}\leq a_{n-1}\leq a_n[/latex]. Želimo dokazati [latex]a_{n+1}\geq a_n[/latex] (možemo reći da je [latex]n>2[/latex]). Sad samo raspiši lijevu i desnu stranu po definicionoj rekurzivnoj relaciji i pogledaj s čime je to ekvivalentno - trebat ćeš razlikovati dva slučaja, kad je [latex]a_{n-1}=0[/latex] i kad nije, ali razlika je zapravo neznatna.
I to je to, gotovi smo :).
Zadatak nije težak, makar zbilja pretjerava s indukcijom  , a budući da smo ga (ili neki iz drugih grupa, a svi su isti) na demonstraturama više puta pokazivali, a pretpostavljam da isto vrijedi i za ostale demonstratore, a i sigurno se tako nešto (ako ne i doslovno ovaj zadatak) radilo na vježbama, možda je sad korisnije da samo neke osnovne korake i zaključke, a onda je na tebi da popuniš rupe i pitaš ako nešto nije jasno , a budući da smo ga (ili neki iz drugih grupa, a svi su isti) na demonstraturama više puta pokazivali, a pretpostavljam da isto vrijedi i za ostale demonstratore, a i sigurno se tako nešto (ako ne i doslovno ovaj zadatak) radilo na vježbama, možda je sad korisnije da samo neke osnovne korake i zaključke, a onda je na tebi da popuniš rupe i pitaš ako nešto nije jasno  . .
Dakle, prvo ćemo "odrediti limes", tj. pretpostavimo da limes postoji i da iznosi  . Onda za njega vrijedi . Onda za njega vrijedi 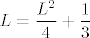 . To je kvadratna jednadžba kojoj su korijeni . To je kvadratna jednadžba kojoj su korijeni 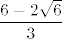 i i 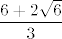 . .
Dokazat ćemo da su svi članovi niza manji od manjeg kandidata za limes, kao i da je niz rastuć. Tada će iz ograničenosti i monotonosti slijediti da je niz konvergentan, a limes će mu biti manji kandidat (da je limes veći kandidat, morali bismo imati članove proizvoljno blizu njemu, a to je nemoguće jer ćemo dokazati da su svi članovi niza manji od manjeg kandidata).
Sad hoćemo dokazati 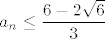 . Ta tvrdnja očito vrijedi za . Ta tvrdnja očito vrijedi za 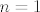 i i  , a dalje nastavljamo jakom indukcijom, tj. pretpostavljamo da tvrdnja vrijedi za , a dalje nastavljamo jakom indukcijom, tj. pretpostavljamo da tvrdnja vrijedi za 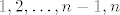 ( (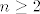 ). ).
(Uzgred, tu implicitno koristimo i da je 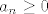 za svaki prirodni za svaki prirodni  , a to je dosta očito da vrijedi, a može se formalno dokazati i indukcijom.) , a to je dosta očito da vrijedi, a može se formalno dokazati i indukcijom.)
Znamo da je sada 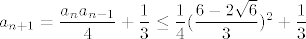 , a kad se to raspiše, dobivamo upravo traženi korak indukcije. , a kad se to raspiše, dobivamo upravo traženi korak indukcije.
Još preostaje pokazati monotonost, tj. da je 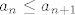 za svaki prirodni za svaki prirodni  . Tvrdnja vrijedi za . Tvrdnja vrijedi za 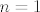 (i, možda nam zatreba, za (i, možda nam zatreba, za  , to lako fizički provjerimo). Sad opet idemo jakom indukcijom i pretpostavljamo , to lako fizički provjerimo). Sad opet idemo jakom indukcijom i pretpostavljamo 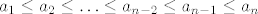 . Želimo dokazati . Želimo dokazati 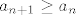 (možemo reći da je (možemo reći da je 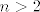 ). Sad samo raspiši lijevu i desnu stranu po definicionoj rekurzivnoj relaciji i pogledaj s čime je to ekvivalentno - trebat ćeš razlikovati dva slučaja, kad je ). Sad samo raspiši lijevu i desnu stranu po definicionoj rekurzivnoj relaciji i pogledaj s čime je to ekvivalentno - trebat ćeš razlikovati dva slučaja, kad je 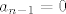 i kad nije, ali razlika je zapravo neznatna. i kad nije, ali razlika je zapravo neznatna.
I to je to, gotovi smo  . .
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:13 sub, 19. 12. 2009 Naslov: Postano: 21:13 sub, 19. 12. 2009 Naslov: |
    |
|
|
Stvari koje ne vrijede malo se teže dokazuju :P :D.
Glavna stvar tu je primijetiti da je [latex]\sinh^2 x\geq 0[/latex], pa mi iz uvjeta eventualno možemo znati da postoji limes zdesna, a o limesu slijeva ne možemo ništa reći. Stoga, uzmi za [latex]f[/latex] funkciju [url=http://en.wikipedia.org/wiki/Sign_function]signum[/url] (tj. njenu restrikciju na [latex]\mathbb{R}\backslash\{0\}[/latex], da budemo precizniji). Ta je funkcija definirana s [latex]\mathrm{sgn} (x)=1[/latex] za [latex]x>0[/latex] i [latex]\mathrm{sgn} (x)=-1[/latex] za [latex]x<0[/latex] (za [latex]0[/latex] bi bila definirana kao [latex]0[/latex], ali to nas tu ne interesira).
Sad očito postoji [latex]\displaystyle \lim_{x\rightarrow 0} f(\sinh^2 x)=\lim_{x\rightarrow 0} \mathrm{sgn} (\sinh^2 x)=1[/latex], ali [latex]\displaystyle \lim_{x\rightarrow 0} f(x)=\lim_{x\rightarrow 0} \mathrm{sgn} (x)[/latex] očito ne postoji. Dakle, našli smo traženi kontraprimjer. Naravno, signum nije jedini kontraprimjer (štoviše, sve funkcije kojima limes zdesna u [latex]0[/latex] nije jednak limesu slijeva u [latex]0[/latex] su kontraprimjeri), ali sam poprilično siguran da je najjednostavniji :).
Stvari koje ne vrijede malo se teže dokazuju   . .
Glavna stvar tu je primijetiti da je 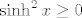 , pa mi iz uvjeta eventualno možemo znati da postoji limes zdesna, a o limesu slijeva ne možemo ništa reći. Stoga, uzmi za , pa mi iz uvjeta eventualno možemo znati da postoji limes zdesna, a o limesu slijeva ne možemo ništa reći. Stoga, uzmi za  funkciju signum (tj. njenu restrikciju na funkciju signum (tj. njenu restrikciju na 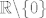 , da budemo precizniji). Ta je funkcija definirana s , da budemo precizniji). Ta je funkcija definirana s 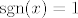 za za 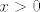 i i 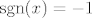 za za 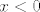 (za (za  bi bila definirana kao bi bila definirana kao  , ali to nas tu ne interesira). , ali to nas tu ne interesira).
Sad očito postoji 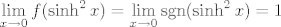 , ali , ali 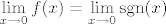 očito ne postoji. Dakle, našli smo traženi kontraprimjer. Naravno, signum nije jedini kontraprimjer (štoviše, sve funkcije kojima limes zdesna u očito ne postoji. Dakle, našli smo traženi kontraprimjer. Naravno, signum nije jedini kontraprimjer (štoviše, sve funkcije kojima limes zdesna u  nije jednak limesu slijeva u nije jednak limesu slijeva u  su kontraprimjeri), ali sam poprilično siguran da je najjednostavniji su kontraprimjeri), ali sam poprilično siguran da je najjednostavniji  . .
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:25 ned, 20. 12. 2009 Naslov: Postano: 14:25 ned, 20. 12. 2009 Naslov: |
    |
|
|
@ante c: Samo ti daj, nema problema :).
@niveus: Ajde ti stavi tu neke zagrade ili nešto, kad ne pišeš u (La)TeX-u. Ja sam našao dva moguća tumačenja toga što ti želiš reći, ali u niti jednom od ta dva slučaja niz nije konvergentan.
Prva opcija je [latex]\displaystyle a_{n+1}=3a_n-\frac{1}{2a_n}[/latex], ali u njoj lako indukcijom pokažemo da vrijedi [latex]a_n\geq n[/latex] za svaki prirodni [latex]n[/latex], pa taj niz ne konvergira (osim ako ne prihvaćaš slučajno divergenciju u beskonačno). Inače, jasno je da [latex](a_n)_n[/latex] raste još i mnogo brže, taj niz generalno izgleda slično kao [latex]3^n[/latex] pomnožen s nekom konstantom, ali to nije sad bitno.
Druga opcija, koja mi se čini manje vjerojatnom, bi bila [latex]\displaystyle a_{n+1}=3a_n-\frac{1}{2}a_n[/latex], ali to je očito isto kao [latex]\displaystyle a_{n+1}=\frac{5}{2}a_n[/latex], pa je [latex]a_n=2\cdot (\frac{5}{2})^{n-1}[/latex] za sve prirodne [latex]n[/latex], što opet ne konvergira u neki realan broj.
Tako da, ako ja nisam nešto zeznuo, ajde malo razjasni zadatak :).
@ante c: Samo ti daj, nema problema  . .
@niveus: Ajde ti stavi tu neke zagrade ili nešto, kad ne pišeš u (La)TeX-u. Ja sam našao dva moguća tumačenja toga što ti želiš reći, ali u niti jednom od ta dva slučaja niz nije konvergentan.
Prva opcija je 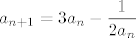 , ali u njoj lako indukcijom pokažemo da vrijedi , ali u njoj lako indukcijom pokažemo da vrijedi  za svaki prirodni za svaki prirodni  , pa taj niz ne konvergira (osim ako ne prihvaćaš slučajno divergenciju u beskonačno). Inače, jasno je da , pa taj niz ne konvergira (osim ako ne prihvaćaš slučajno divergenciju u beskonačno). Inače, jasno je da 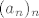 raste još i mnogo brže, taj niz generalno izgleda slično kao raste još i mnogo brže, taj niz generalno izgleda slično kao  pomnožen s nekom konstantom, ali to nije sad bitno. pomnožen s nekom konstantom, ali to nije sad bitno.
Druga opcija, koja mi se čini manje vjerojatnom, bi bila 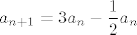 , ali to je očito isto kao , ali to je očito isto kao 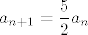 , pa je , pa je 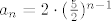 za sve prirodne za sve prirodne  , što opet ne konvergira u neki realan broj. , što opet ne konvergira u neki realan broj.
Tako da, ako ja nisam nešto zeznuo, ajde malo razjasni zadatak  . .
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:27 ned, 20. 12. 2009 Naslov: Postano: 14:27 ned, 20. 12. 2009 Naslov: |
    |
|
|
[quote="niveus"]Niz je zadan rekurzivno, treba pokazati da je konvergentan i odrediti mu limes a1=2, a(n+1)=3an-1/2an za n>=1[/quote]
Sve isto kao gore rekao bih :D
Nađeš kandidata za limes (rješenja kvadratne jedn su 1 i 1/2), 1 će bit naš kandidat (ispiši prvih par članova niza, i vidi se da su sve bliže jedinici, i da padaju), pa se pokaže da je niz padajuć, i da je ograničen odozdo sa 1, što daje konvergenciju k 1 :D
edit : ja sam razumio kao: [latex]a_{n+1} = \frac{3 a_n-1}{2a_n}[/latex]
| niveus (napisa): | | Niz je zadan rekurzivno, treba pokazati da je konvergentan i odrediti mu limes a1=2, a(n+1)=3an-1/2an za n>=1 |
Sve isto kao gore rekao bih 
Nađeš kandidata za limes (rješenja kvadratne jedn su 1 i 1/2), 1 će bit naš kandidat (ispiši prvih par članova niza, i vidi se da su sve bliže jedinici, i da padaju), pa se pokaže da je niz padajuć, i da je ograničen odozdo sa 1, što daje konvergenciju k 1 
edit : ja sam razumio kao: 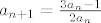
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:36 ned, 20. 12. 2009 Naslov: Postano: 14:36 ned, 20. 12. 2009 Naslov: |
    |
|
|
Ahaaa :D. Vidiš kako su te zagrade korisna stvar :lol:. (Ja bih ovo uvijek bez TeXa napisao kao a_(n+1)=3/2-1/(2a_n).)
Da, priča je zbilja ista kao u zadatku prije, samo što je nešto lakša budući da se koristi "obična", a ne jaka indukcija. Dakle, probaj postupiti kako je Luuka rekao i kako piše u gornjoj ideji (odredi kandidate za limes - odaberi onog koji ti se čini smislen - dokaži monotonost i ograničenost (ograničenost u smislu da odmah i eliminiraš drugog kandidata)), pa javi ako negdje zapneš :).
Ahaaa  . Vidiš kako su te zagrade korisna stvar . Vidiš kako su te zagrade korisna stvar  . (Ja bih ovo uvijek bez TeXa napisao kao a_(n+1)=3/2-1/(2a_n).) . (Ja bih ovo uvijek bez TeXa napisao kao a_(n+1)=3/2-1/(2a_n).)
Da, priča je zbilja ista kao u zadatku prije, samo što je nešto lakša budući da se koristi "obična", a ne jaka indukcija. Dakle, probaj postupiti kako je Luuka rekao i kako piše u gornjoj ideji (odredi kandidate za limes - odaberi onog koji ti se čini smislen - dokaži monotonost i ograničenost (ograničenost u smislu da odmah i eliminiraš drugog kandidata)), pa javi ako negdje zapneš  . .
|
|
| [Vrh] |
|
|





