| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
 Postano: 12:36 ned, 20. 12. 2009 Naslov: Postano: 12:36 ned, 20. 12. 2009 Naslov: |
    |
|
|
ja bi isto zamolio ak neko moze pomoc
16. Dan je kvadrat ABCD stranice duljine a. To·cke K, L, M i N polovi·sta su stranica
AB, BC, CD, AD redom. Odredite povr·sinu kvadrata kojeg omeduju pravci AM,
BN, CK i DL.
ja bi isto zamolio ak neko moze pomoc
16. Dan je kvadrat ABCD stranice duljine a. To·cke K, L, M i N polovi·sta su stranica
AB, BC, CD, AD redom. Odredite povr·sinu kvadrata kojeg omeduju pravci AM,
BN, CK i DL.
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
BeeBee
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (16:07:39)
Postovi: (79)16
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
z3h
Forumaš(ica)
Pridružen/a: 05. 10. 2004. (22:26:02)
Postovi: (46)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
Wolfert
Forumaš(ica)


Pridružen/a: 24. 10. 2006. (12:27:01)
Postovi: (42)16
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 18:46 ned, 20. 12. 2009 Naslov: Postano: 18:46 ned, 20. 12. 2009 Naslov: |
    |
|
|
[quote="Glupko_3.14"][quote="kenny"]Konstuiraj kao konstrukciju proporcionale. Zamisli da ti piše [latex]a \sqrt{6} = 1 \cdot b[/latex]. Rješenje ti je upravo ovaj b. ;)[/quote]
ja ovo ne razumijem? sto je to proporcionala?
a mozes i imat jednu stranicu 2a, drugu pod pravim kutom a, pa dobijes korijen iz 5 * a, i onda jos jednom pa dobijes korijen iz 6 a
jel to isto si ti kenny rekao?[/quote]
Može i tako, a možeš konstruirati i kao četvrtu proporcionalu. Malo transformirajmo:
[latex]a \cdot \sqrt{6} = 1 \cdot b\\
\frac{a}{1} = \frac{b}{\sqrt{6}}[/latex]
Poanta je u sličnosti trokuta. Stranica a se odnosi prema stranici duljine 1 kao što se stranica b (koja je tražena) odnosi prema stranici duljine [latex]\sqrt{6}[/latex] ;)
Pogledaj GGB fajl u prilogu!
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
[quote="gogo_"]
4. Kateta pravokutnog trokuta je za 3 dulja od svoje ortogonalne projekcije na hipotenuzu,
a duljina projekcije druge katete na hipotenuzu iznosi 15. Odredi duljine stranica
trokuta.
[/quote]
Gogo....u pravokutnom trokutu vrijedi da je visina na hipotenuzu geometrijska sredina dijelova na koji visina dijeli hipotenuzu. Jasno je da u ovom tvom zadatku visina dijeli hipotenuzu na dva dijela [latex]b' = 15, a' = x[/latex], pa prema tome vrijedi [latex]v = \sqrt{15x}[/latex]. Također vrijedi i [latex](3+x)^2 = v^2+x^2[/latex] (Pitagorin poučak za trokut određen visinom pravokutnog trokuta, jednom katetom i ortogonalnom projekcijom te katete na hipotenuzu).
Dakle, imaš sustav:
[latex]v = \sqrt{15x} \\
(3+x)^2=v^2+x^2[/latex]
Poprilično jednostavan sustav. Kad ga riješiš dobiješ [latex]x = 1[/latex]. Pa je [latex]a = 4, c = 16[/latex].
Drugu katetu možeš računati ili preko Pitagorinog poučka ili preko činjenice da je kateta pravokutnog trokuta geometrijska sredina hipotenuze i svoje ortogonalne projekcije na hipotenuzu, odnosno: [latex]b = \sqrt{c\cdot b'}[/latex]. Uvrstiš i dobiješ [latex]b=4\sqrt{15}[/latex].
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
@pravopurger: evo dio tvog zadatka (udaljenost sjecišta dijagonala do osnovica):
Nacrtaj trapez ABCCD i dijagonale koje se sijeku u toki E. Lako se vidi da su trokuti ABE i CDE slični (kutovi koje dijagonale zatvaraju sa osnovicama su jednaki!), pa vrijedi proporcionalnost [latex]a:b = v_1:v_2[/latex], gdje su [latex]v_1, v_2[/latex] visine trokuta ABE i CDE. Sa druge strane znamo da je visina trapeza [latex]v=c[/latex], odnosno [latex]v_1+v_2 = c[/latex]. Kako su a, b, c poznati, imaš sustav dvije jednadžbe sa dvije nepoznanice. Rješavanjem dobiješ [latex]v_1[/latex] što je udaljenost sjecišta dijagonala od osnovice a i [latex]v_2[/latex] što je udaljenost sjecišta dijagonala od osnovice b... Dobiješ [latex]v_1 = \frac{ac}{a+b}, v_2 = \frac{bc}{a+b}[/latex].
| Glupko_3.14 (napisa): | | kenny (napisa): | Konstuiraj kao konstrukciju proporcionale. Zamisli da ti piše  . Rješenje ti je upravo ovaj b. . Rješenje ti je upravo ovaj b.  |
ja ovo ne razumijem? sto je to proporcionala?
a mozes i imat jednu stranicu 2a, drugu pod pravim kutom a, pa dobijes korijen iz 5 * a, i onda jos jednom pa dobijes korijen iz 6 a
jel to isto si ti kenny rekao? |
Može i tako, a možeš konstruirati i kao četvrtu proporcionalu. Malo transformirajmo:
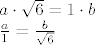
Poanta je u sličnosti trokuta. Stranica a se odnosi prema stranici duljine 1 kao što se stranica b (koja je tražena) odnosi prema stranici duljine 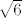 
Pogledaj GGB fajl u prilogu!
Added after 16 minutes:
| gogo_ (napisa): |
4. Kateta pravokutnog trokuta je za 3 dulja od svoje ortogonalne projekcije na hipotenuzu,
a duljina projekcije druge katete na hipotenuzu iznosi 15. Odredi duljine stranica
trokuta.
|
Gogo....u pravokutnom trokutu vrijedi da je visina na hipotenuzu geometrijska sredina dijelova na koji visina dijeli hipotenuzu. Jasno je da u ovom tvom zadatku visina dijeli hipotenuzu na dva dijela 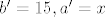 , pa prema tome vrijedi , pa prema tome vrijedi 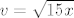 . Također vrijedi i . Također vrijedi i 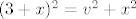 (Pitagorin poučak za trokut određen visinom pravokutnog trokuta, jednom katetom i ortogonalnom projekcijom te katete na hipotenuzu). (Pitagorin poučak za trokut određen visinom pravokutnog trokuta, jednom katetom i ortogonalnom projekcijom te katete na hipotenuzu).
Dakle, imaš sustav:
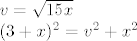
Poprilično jednostavan sustav. Kad ga riješiš dobiješ  . Pa je . Pa je 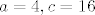 . .
Drugu katetu možeš računati ili preko Pitagorinog poučka ili preko činjenice da je kateta pravokutnog trokuta geometrijska sredina hipotenuze i svoje ortogonalne projekcije na hipotenuzu, odnosno: 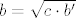 . Uvrstiš i dobiješ . Uvrstiš i dobiješ 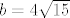 . .
Added after 13 minutes:
@pravopurger: evo dio tvog zadatka (udaljenost sjecišta dijagonala do osnovica):
Nacrtaj trapez ABCCD i dijagonale koje se sijeku u toki E. Lako se vidi da su trokuti ABE i CDE slični (kutovi koje dijagonale zatvaraju sa osnovicama su jednaki!), pa vrijedi proporcionalnost 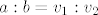 , gdje su , gdje su 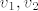 visine trokuta ABE i CDE. Sa druge strane znamo da je visina trapeza visine trokuta ABE i CDE. Sa druge strane znamo da je visina trapeza  , odnosno , odnosno 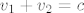 . Kako su a, b, c poznati, imaš sustav dvije jednadžbe sa dvije nepoznanice. Rješavanjem dobiješ . Kako su a, b, c poznati, imaš sustav dvije jednadžbe sa dvije nepoznanice. Rješavanjem dobiješ 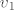 što je udaljenost sjecišta dijagonala od osnovice a i što je udaljenost sjecišta dijagonala od osnovice a i 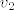 što je udaljenost sjecišta dijagonala od osnovice b... Dobiješ što je udaljenost sjecišta dijagonala od osnovice b... Dobiješ 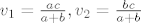 . .
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
| Description: |
|

Download |
| Filename: |
4prop.zip |
| Filesize: |
3.57 KB |
| Downloaded: |
193 Time(s) |
|
|
| [Vrh] |
|
z3h
Forumaš(ica)
Pridružen/a: 05. 10. 2004. (22:26:02)
Postovi: (46)16
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
sylar
Forumaš(ica)
Pridružen/a: 13. 10. 2008. (17:42:14)
Postovi: (5F)16
|
 Postano: 22:28 ned, 20. 12. 2009 Naslov: Postano: 22:28 ned, 20. 12. 2009 Naslov: |
    |
|
|
zadatk 18..konstrukcija a√6
se može jako jednostavno riješit, evo ovako:
konstruira se jednakostraničan pravokutan trokut s katetama duljine a, pa je hipotenuza a√2, zatim se povuče okomica na hipotenuzu iz vrha A ili B duljine 2a, pa imamo pravokutan trokut s katetama duljina a√2 i 2a, a onda hipotenuza iznosi a√6
i to je to, ne trebate ništa koristiti iz kolegija Konstruktivne metode u geometriji, to će te slušati na drugoj god, ima vremena za to
pozzzz :wink:
zadatk 18..konstrukcija a√6
se može jako jednostavno riješit, evo ovako:
konstruira se jednakostraničan pravokutan trokut s katetama duljine a, pa je hipotenuza a√2, zatim se povuče okomica na hipotenuzu iz vrha A ili B duljine 2a, pa imamo pravokutan trokut s katetama duljina a√2 i 2a, a onda hipotenuza iznosi a√6
i to je to, ne trebate ništa koristiti iz kolegija Konstruktivne metode u geometriji, to će te slušati na drugoj god, ima vremena za to
pozzzz 
_________________
...we die and world will be poor for it...
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
|











