| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Junky099
Forumaš(ica)
Pridružen/a: 16. 09. 2009. (12:17:46)
Postovi: (24)16
Spol: 
Lokacija: Novi Zagreb
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 20:56 ned, 20. 12. 2009 Naslov: Postano: 20:56 ned, 20. 12. 2009 Naslov: |
    |
|
|
taj x prikazes rastavljenog na proste faktore - x=p_1^a_1*...*p_k^a_k
onda, eulerova funkcija od x je jednaka f(x)=x*(1- 1/p_1)*...*(1- 1/p_k) = p_1^(a_1-1)*(p_1 - 1)*...*p_k^(a_k-1)*(p_k - 1) = 14
onda vidis da posto (p_i-1) dijeli 14, slijedi da je p_i -1 iz skupa {1,2,7,14}, odnosno p_i iz {2,3,8,15}, i jos p_i mora biti prost pa je zapravo p_i iz {2,3}
znaci x=2^a_1 * 3^a_2
14=f(x)=2^(a_1 -1)* )*1*3^(a_2-1)*2
7=2^(a_1-1)*3(a_2-1), a to očito nema rješenja u prirodnim brojevima
taj x prikazes rastavljenog na proste faktore - x=p_1^a_1*...*p_k^a_k
onda, eulerova funkcija od x je jednaka f(x)=x*(1- 1/p_1)*...*(1- 1/p_k) = p_1^(a_1-1)*(p_1 - 1)*...*p_k^(a_k-1)*(p_k - 1) = 14
onda vidis da posto (p_i-1) dijeli 14, slijedi da je p_i -1 iz skupa {1,2,7,14}, odnosno p_i iz {2,3,8,15}, i jos p_i mora biti prost pa je zapravo p_i iz {2,3}
znaci x=2^a_1 * 3^a_2
14=f(x)=2^(a_1 -1)* )*1*3^(a_2-1)*2
7=2^(a_1-1)*3(a_2-1), a to očito nema rješenja u prirodnim brojevima
|
|
| [Vrh] |
|
Junky099
Forumaš(ica)
Pridružen/a: 16. 09. 2009. (12:17:46)
Postovi: (24)16
Spol: 
Lokacija: Novi Zagreb
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:19 uto, 22. 12. 2009 Naslov: Postano: 23:19 uto, 22. 12. 2009 Naslov: |
    |
|
|
[latex]n^2 + \left(n+1\right)^2 + \left(n+2\right)^2 + \left(n+3\right)^2 = 4n^2 + 12n + 14 = 2\left(2n^2 + 6n + 7\right)[/latex], iz ovog slijedi da moramo naći [latex]n[/latex] za koji je [latex]2n^2 + 6n + 7[/latex] djeljivo s [latex]5[/latex].
Vrijedi [latex]2n^2 + 6n + 7 = 5\left(n + 1\right) + 2n^2 + n + 2[/latex], dakle, potrebno je naći [latex]n[/latex] za koji je [latex]2n^2 + n + 2 = n\left(2n+1\right)+2[/latex] djeljivo s 5.
Sada direktnom provjerom vidimo da zadovoljavaju svi (i samo oni!) brojevi oblika [latex]n = 5k + 1[/latex], gdje je [latex]k \in \mathbb{Z}[/latex], odnosno [latex]k \in \mathbb{N} \cup \left\{0\right\}[/latex] ukoliko [latex]n[/latex] mora biti prirodan broj.
 , iz ovog slijedi da moramo naći , iz ovog slijedi da moramo naći  za koji je za koji je  djeljivo s djeljivo s  . .
Vrijedi 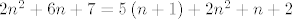 , dakle, potrebno je naći , dakle, potrebno je naći  za koji je za koji je 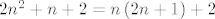 djeljivo s 5. djeljivo s 5.
Sada direktnom provjerom vidimo da zadovoljavaju svi (i samo oni!) brojevi oblika 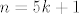 , gdje je , gdje je 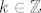 , odnosno , odnosno 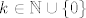 ukoliko ukoliko  mora biti prirodan broj. mora biti prirodan broj.
|
|
| [Vrh] |
|
|








