|
Pogledamo polinom q(x)=p(x)-7. Taj je ocito iz Z[x] i ima barem 4 razlicite cjelobrojne nultocke (neka su to a, b, c, d).
Zbog toga ga mozemo faktorizirati u ovaj oblik:
q(x)=(x-a)(x-b)(x-c)(x-d)*r(x), gdje je r(x) neki polinom iz Z(x)*
*(strogo govoreci, cinjenicu da je R iz Z[x] bi trebalo dokazati jer (barem mi se tako cini) nije bas ocita, ali taj dio dokaza je na kraju radi preglednosti)
Ugl sad, kad imamo ovakav (pomocni) q, mozemo p zapisati kao
p(x)=(x-a)(x-b)(x-c)(x-d)*r(x) + 7. Pretpostavimo sada da postoji cijeli broj k za koji p(x) postize vrijednost 14. Tada imamo:
p(k)=(k-a)(k-b)(k-c)(k-d)*r(k) + 7 = 14, tj.
[b](k-a)(k-b)(k-c)(k-d)*r(k) = 7[/b]. Iz ovoga vidimo da su [u]cijeli[/u] brojevi (k-a), (k-b), (k-c), (k-d) (razliciti) djelitelji broja 7.
Uocimo, cjelobrojni djelitelji broja 7 su -1, 1, -7, 7, pa, buduci da imamo 4 razlicita djelitelja, mozemo zakljuciti da su k-a, k-b, k-c, k-d upravo brojevi -1, 1, -7, 7. (u bilokojem poretku)
Zbog toga je njihov umnozak (k-a)(k-b)(k-c)(k-d)=(-1)*1*(-7)*7=49, pa ako uvrstimo to u gornju jednakost (boldanu), dobivamo 49*r(k)=7,
to jest r(k)=1/7, sto je kontradikcija s tvrdnjom da je r iz Z[x] (jer polinomi iz Z[x] u cjelobrojnim tockama poprimaju cjelobrojne vrijednosti) => gotov dokaz
*Jos samo dokaz tvrdnje da je r iz Z[x]:
Neka je [latex]p \in \mathbb{Z}[x][/latex] polinom s nultockom [latex]k \in \mathbb{Z}[x][/latex].
Zbog toga p(x) mozemo zapisati kao (x-k)r(x). Dokazujemo da je tada [latex]r \in \mathbb{Z}[x][/latex].
Zapisimo r u obliku [latex]r=a_nx^{n-1}+a_{n-1}x^{n-2}+ \dots + a_2x + a_1[/latex] Iz toga dobijemo
[latex]p(x)=(x-k)(a_nx^{n-1}+a_{n-1}x^{n-2}+\dots+a_2x+a_1) =[/latex]
[latex]a_nx^n+(a_{n-1}-ka_n)x^{n-1}+\dots+(a_1-ka_2)x-ka_1[/latex]
Sad smo zapisali p(x), a za njega znamo da su mu svi koef. cijeli brojevi, pa imamo:
[latex]a_n \in \mathbb{Z}[/latex].
[latex]a_{n-1}-ka_n \in \mathbb{Z}[/latex]
[latex]\vdots[/latex] (itd)
Sada redom dobivamo da su koeficijenti polinoma r, [latex]a_i[/latex] iz Z:
[latex]a_n \in \mathbb{Z}[/latex] pa je [latex]ka_n \in \mathbb{Z}[/latex], a kako je [latex]a_{n-1}-ka_n \in \mathbb{Z}[/latex], mora biti [latex]a_{n-1} \in \mathbb{Z}[/latex].
Argumentaciju nastavljamo (u drugom koraku idemo od [latex]a_{n-1} \in \mathbb{Z}[/latex]) i vidimo da su svi koeficijenti polinoma r u Z
Pogledamo polinom q(x)=p(x)-7. Taj je ocito iz Z[x] i ima barem 4 razlicite cjelobrojne nultocke (neka su to a, b, c, d).
Zbog toga ga mozemo faktorizirati u ovaj oblik:
q(x)=(x-a)(x-b)(x-c)(x-d)*r(x), gdje je r(x) neki polinom iz Z(x)*
*(strogo govoreci, cinjenicu da je R iz Z[x] bi trebalo dokazati jer (barem mi se tako cini) nije bas ocita, ali taj dio dokaza je na kraju radi preglednosti)
Ugl sad, kad imamo ovakav (pomocni) q, mozemo p zapisati kao
p(x)=(x-a)(x-b)(x-c)(x-d)*r(x) + 7. Pretpostavimo sada da postoji cijeli broj k za koji p(x) postize vrijednost 14. Tada imamo:
p(k)=(k-a)(k-b)(k-c)(k-d)*r(k) + 7 = 14, tj.
(k-a)(k-b)(k-c)(k-d)*r(k) = 7. Iz ovoga vidimo da su cijeli brojevi (k-a), (k-b), (k-c), (k-d) (razliciti) djelitelji broja 7.
Uocimo, cjelobrojni djelitelji broja 7 su -1, 1, -7, 7, pa, buduci da imamo 4 razlicita djelitelja, mozemo zakljuciti da su k-a, k-b, k-c, k-d upravo brojevi -1, 1, -7, 7. (u bilokojem poretku)
Zbog toga je njihov umnozak (k-a)(k-b)(k-c)(k-d)=(-1)*1*(-7)*7=49, pa ako uvrstimo to u gornju jednakost (boldanu), dobivamo 49*r(k)=7,
to jest r(k)=1/7, sto je kontradikcija s tvrdnjom da je r iz Z[x] (jer polinomi iz Z[x] u cjelobrojnim tockama poprimaju cjelobrojne vrijednosti) ⇒ gotov dokaz
*Jos samo dokaz tvrdnje da je r iz Z[x]:
Neka je 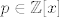 polinom s nultockom polinom s nultockom 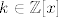 . .
Zbog toga p(x) mozemo zapisati kao (x-k)r(x). Dokazujemo da je tada 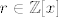 . .
Zapisimo r u obliku 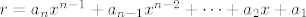 Iz toga dobijemo Iz toga dobijemo
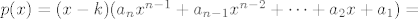
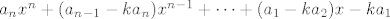
Sad smo zapisali p(x), a za njega znamo da su mu svi koef. cijeli brojevi, pa imamo:
 . .
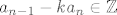
 (itd) (itd)
Sada redom dobivamo da su koeficijenti polinoma r, 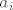 iz Z: iz Z:
 pa je pa je 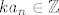 , a kako je , a kako je 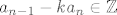 , mora biti , mora biti 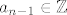 . .
Argumentaciju nastavljamo (u drugom koraku idemo od 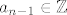 ) i vidimo da su svi koeficijenti polinoma r u Z ) i vidimo da su svi koeficijenti polinoma r u Z
|






