| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
(s)Venn
Forumaš(ica)

Pridružen/a: 18. 02. 2009. (17:59:25)
Postovi: (40)16
Lokacija: Velika Gorica
|
 Postano: 12:48 uto, 29. 12. 2009 Naslov: Postano: 12:48 uto, 29. 12. 2009 Naslov: |
    |
|
|
Molim vas da mi razjasnite kako odrediti funkciju gustoće u zadatku 6.32 koji se nalazi [url=http://web.math.hr/nastava/uuv/files/chap6.pdf]ovdje[/url] (17. str.)
Zahvaljujem unaprijed. :wink:
Molim vas da mi razjasnite kako odrediti funkciju gustoće u zadatku 6.32 koji se nalazi ovdje (17. str.)
Zahvaljujem unaprijed. 
_________________ ..pišem pjesme, sviram bluz, radost i tugu na stihove lomim.. |
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:30 uto, 5. 1. 2010 Naslov: Postano: 1:30 uto, 5. 1. 2010 Naslov: |
    |
|
|
Preformuliramo malo zadatak, tražiti ćemo najmanji [latex]n[/latex] (broj ljudi puštenih u dvorac) takav da s vjerojatnošću većom od [latex]0.95[/latex] u dvorac uđe barem [latex]500-n[/latex] plemića. Naime, svatko ko uđe u dvorac da barem jedan zlatnik, pa gledamo zadatak kao da svaki plemić daje po jedan, a građanin nijedan zlatnik. Formuliramo.
[latex]n=[/latex] broj uzvanika,
[latex]X=[/latex] broj plemića među uzvanicima, dakle
[latex]X \sim B\left(n,\, \frac{1}{4}\right) [/latex],
[latex]np = \frac{n}{4}[/latex], [latex]npq = \frac{3n}{4}[/latex].
Moramo naći [latex]n[/latex] takav da je
[latex]0.95 \leq P\left(X \geq 500-n\right) = P\left(500-n \leq X \leq n\right) \approx \Phi\left(\frac{n - \frac{n}{4}}{\frac{\sqrt{3n}}{2}}\right) - \Phi\left(\frac{500-n-\frac{n}{4}}{\frac{\sqrt{3n}}{2}}\right) \approx[/latex]
[latex]\approx1 - \Phi\left(\frac{5}{2} \cdot \frac{400-n}{\sqrt{3n}}\right) \Longrightarrow \Phi\left(\frac{5}{2} \cdot \frac{400 - n}{\sqrt{3n}}\right) \leq 0.05[/latex].
[latex]\Phi\left(-1.65\right) = 0.05 \Longrightarrow 5n - 5.7157\sqrt{n} - 2000 \geq 0 \Longrightarrow n \geq 423.53[/latex].
Dakle, u dvorac mora ući barem [latex]424[/latex] ljudi.
Preformuliramo malo zadatak, tražiti ćemo najmanji  (broj ljudi puštenih u dvorac) takav da s vjerojatnošću većom od (broj ljudi puštenih u dvorac) takav da s vjerojatnošću većom od 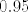 u dvorac uđe barem u dvorac uđe barem 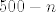 plemića. Naime, svatko ko uđe u dvorac da barem jedan zlatnik, pa gledamo zadatak kao da svaki plemić daje po jedan, a građanin nijedan zlatnik. Formuliramo. plemića. Naime, svatko ko uđe u dvorac da barem jedan zlatnik, pa gledamo zadatak kao da svaki plemić daje po jedan, a građanin nijedan zlatnik. Formuliramo.
 broj uzvanika, broj uzvanika,
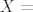 broj plemića među uzvanicima, dakle broj plemića među uzvanicima, dakle
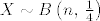 , ,
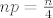 , , 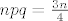 . .
Moramo naći  takav da je takav da je
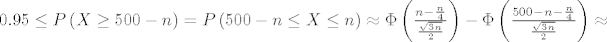
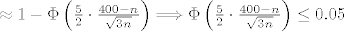 . .
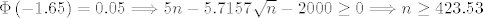 . .
Dakle, u dvorac mora ući barem 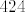 ljudi. ljudi.
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 18:28 pet, 15. 1. 2010 Naslov: Postano: 18:28 pet, 15. 1. 2010 Naslov: |
    |
|
|
rekao bih da je X - B (150, 0,25) i da treba naći vjerojatnost da je X >= 100.
nije zicer, al zvuči mi logično
rekao bih da je X - B (150, 0,25) i da treba naći vjerojatnost da je X >= 100.
nije zicer, al zvuči mi logično
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 20:43 pet, 15. 1. 2010 Naslov: Postano: 20:43 pet, 15. 1. 2010 Naslov: |
    |
|
|
[quote="Vip"]slažem se da je X - B(150, 0.25) ali ne znam baš za X>=100.. :([/quote]
mora ih bit bar duplo više sa biserima.
daklem, od 150 sve su il sa il bez bisera. ak ovih bez bisera ima više od pedeset, moš ga slikat, nikad neće izać da ovih sa biserima ima dvaput tolko (jer bi ih onda trebalo više bit).
sad, kak to izračunat? znam da je tražena vjerojatnost 1 - P (X < 100). daklem, kak da računam ove povrhe? sumu svih njih, to me zeza
e da, i može, ak je neko rješavo. zadatak kaže: X je geom sluč var s parametrom p. dokaži da je E (1/X) = (-p * ln p)/ (1 - p)
riješio sam to, al nisam nikak mogao dobiti ovaj minus ispred. je dab tak trebalo biti, jer je ln (p) manji od nule, al nisam ga uspio dobiti
| Vip (napisa): | slažem se da je X - B(150, 0.25) ali ne znam baš za X>=100..  |
mora ih bit bar duplo više sa biserima.
daklem, od 150 sve su il sa il bez bisera. ak ovih bez bisera ima više od pedeset, moš ga slikat, nikad neće izać da ovih sa biserima ima dvaput tolko (jer bi ih onda trebalo više bit).
sad, kak to izračunat? znam da je tražena vjerojatnost 1 - P (X < 100). daklem, kak da računam ove povrhe? sumu svih njih, to me zeza
e da, i može, ak je neko rješavo. zadatak kaže: X je geom sluč var s parametrom p. dokaži da je E (1/X) = (-p * ln p)/ (1 - p)
riješio sam to, al nisam nikak mogao dobiti ovaj minus ispred. je dab tak trebalo biti, jer je ln (p) manji od nule, al nisam ga uspio dobiti
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 13:50 sub, 16. 1. 2010 Naslov: Postano: 13:50 sub, 16. 1. 2010 Naslov: |
    |
|
|
može uputa za zad 6.26(znam da je X-N(40,15),ali neznam kako postavit zad,
6.29, 6.30,6.31?
6.38,je li to binomna B(160,0.9),pa trebam izračunat P(X>150)?
može uputa za zad 6.26(znam da je X-N(40,15),ali neznam kako postavit zad,
6.29, 6.30,6.31?
6.38,je li to binomna B(160,0.9),pa trebam izračunat P(X>150)?
|
|
| [Vrh] |
|
Alisa
Forumaš(ica)
Pridružen/a: 16. 02. 2008. (15:34:59)
Postovi: (4E)16
|
 Postano: 21:28 sub, 16. 1. 2010 Naslov: Postano: 21:28 sub, 16. 1. 2010 Naslov: |
    |
|
|
Zad 6.29.
X~N(mi, sigma^2) => EX=mi =>5=mi
Nadalje ,treba odrediti sigma (u daljnjem tekstu S).
0.2=P(X>9)= 1-P(X<=9)=(sad izraz u zagradi normiraj, tj. svedi na jediničnu normalnu razdiobu).....trebala bi dobiti 0.2=P(X-5/S<=9-5/S) =>
fi(0.84)=fi(9-5/S) => 0.84=4/S => S=100/21
Var X=S^2= (100/21)^2....i to je to!
Zad 6.31.
a) Da bi odredila c treba vrijediti 1=integral (-besk. do + besk.) f(x)dx
U našem slučaju to je integral od 0 do +beskonačno (cx^2e^-ax)dx. Sad taj integral riješiš (imaš dva puta parcijalnu integraciju).....i dobiva se (bar sam ja tako dobila) 1=2c/a^3 => c=(a^3)/2
b) P(0<X<1/a)= integral (0 do 1/a) ( (a^3)/2*x^2e^-ax)....riješi se taj integral...Ja sam dobila (-1/2e)- (2/e)+1 =0.0803
Zad 6.38.
Da, binomna je B(160, 0.9) i trebaš izračunat P(X>150)=1-P(X<=150)....
Ove ostale ne znam.
P.S. Ispričavam se što ne znam pisat u Latexu. Potrudit ću se to naučit što prije! )
Zad 6.29.
X~N(mi, sigma^2) => EX=mi =>5=mi
Nadalje ,treba odrediti sigma (u daljnjem tekstu S).
0.2=P(X>9)= 1-P(X<=9)=(sad izraz u zagradi normiraj, tj. svedi na jediničnu normalnu razdiobu).....trebala bi dobiti 0.2=P(X-5/S<=9-5/S) =>
fi(0.84)=fi(9-5/S) => 0.84=4/S => S=100/21
Var X=S^2= (100/21)^2....i to je to!
Zad 6.31.
a) Da bi odredila c treba vrijediti: 1=integral (-besk. do + besk.) f(x)dx
U našem slučaju to je integral od 0 do +beskonačno (cx^2e^-ax)dx. Sad taj integral riješiš (imaš dva puta parcijalnu integraciju).....i dobiva se (bar sam ja tako dobila) 1=2c/a^3 => c=(a^3)/2
b) P(0<X<1/a)= integral (0 do 1/a) ( (a^3)/2*x^2e^-ax)....riješi se taj integral...Ja sam dobila (-1/2e)- (2/e)+1 =0.0803
Zad 6.38.
Da, binomna je B(160, 0.9) i trebaš izračunat P(X>150)=1-P(X<=150)....
Ove ostale ne znam.
P.S. Ispričavam se što ne znam pisat u Latexu. Potrudit ću se to naučit što prije! 
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
 Postano: 4:28 ned, 17. 1. 2010 Naslov: Postano: 4:28 ned, 17. 1. 2010 Naslov: |
    |
|
|
[quote=".anchy."]može uputa za zad 6.26(znam da je X-N(40,15),ali neznam kako postavit zad,
6.29, 6.30,6.31?
6.38,je li to binomna B(160,0.9),pa trebam izračunat P(X>150)?[/quote]
6.26
neka je X broj bodova
imamo normalnu distribuciju X (76,15^2)
nas zanima P (X>n)<=0.15.
znači 15 posto studenata dobija 5icu...recimo da slučajno odabereš tih 15 studenata...šansa da će pojedinac dobit je manja ili jednaka .15....tako i ovo...tražiš takvu granicu n, takvu da kad slučajnu odabereš neki broj, da je taj broj s vjerojatnošću od 85 posto manji od n ( ostale ocjene) a 15 posto veći od n (petice)...
nakon sređivanja... P(X<=n)>=0.85 ( a možeš počet i od ove pretpostavke u biti :D ) a sada pogledaš u tablicu...i izračunaš n....
nemam to sada ali tražiš fi na minus prvu od 0.85....i to ti je jednako n- ni/ standardna devijacija .... (svođenje na jediničnu razdiobu)
6.30
što govori zadatak.imaš normalnu razdiobu godišnjih padalina s očekivanjem 40 cm....znači ti svake godine godine očekuješ 40 cm i imaš Var X koji mjeri odstupanje i to je 4...
pita se kolika je vjerojatnost da ćeš čekati dulje od 10 godina da razina pređe 50 cm..
pa to znači da u ovih 10 godina, ne smije preći razinu od 50...a kako svake godine vrijedi sve "ispočetka"
to ti je P(x<=50)^10 = P(x1<=(50-40)/4) = FI (2.5)^10
| .anchy. (napisa): | može uputa za zad 6.26(znam da je X-N(40,15),ali neznam kako postavit zad,
6.29, 6.30,6.31?
6.38,je li to binomna B(160,0.9),pa trebam izračunat P(X>150)? |
6.26
neka je X broj bodova
imamo normalnu distribuciju X (76,15^2)
nas zanima P (X>n)⇐0.15.
znači 15 posto studenata dobija 5icu...recimo da slučajno odabereš tih 15 studenata...šansa da će pojedinac dobit je manja ili jednaka .15....tako i ovo...tražiš takvu granicu n, takvu da kad slučajnu odabereš neki broj, da je taj broj s vjerojatnošću od 85 posto manji od n ( ostale ocjene) a 15 posto veći od n (petice)...
nakon sređivanja... P(X⇐n)>=0.85 ( a možeš počet i od ove pretpostavke u biti  ) a sada pogledaš u tablicu...i izračunaš n.... ) a sada pogledaš u tablicu...i izračunaš n....
nemam to sada ali tražiš fi na minus prvu od 0.85....i to ti je jednako n- ni/ standardna devijacija .... (svođenje na jediničnu razdiobu)
6.30
što govori zadatak.imaš normalnu razdiobu godišnjih padalina s očekivanjem 40 cm....znači ti svake godine godine očekuješ 40 cm i imaš Var X koji mjeri odstupanje i to je 4...
pita se kolika je vjerojatnost da ćeš čekati dulje od 10 godina da razina pređe 50 cm..
pa to znači da u ovih 10 godina, ne smije preći razinu od 50...a kako svake godine vrijedi sve "ispočetka"
to ti je P(x⇐50)^10 = P(x1⇐(50-40)/4) = FI (2.5)^10
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
Alisa
Forumaš(ica)
Pridružen/a: 16. 02. 2008. (15:34:59)
Postovi: (4E)16
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
 Postano: 21:36 ned, 17. 1. 2010 Naslov: Postano: 21:36 ned, 17. 1. 2010 Naslov: |
    |
|
|
za 5.6 a) gledaš napraviš tablicu x * y koja će biti 3 *2 jer X^2 poprima vrijednosti 0 i 1...
a ako gledaš recimo član matrice u kojem je X = 0 a Y=-1 pri čemu je Y= x^2 to je očito nemoguće
ako gledaš da je X=0 Y=0 to je isto onome elementarnom događaju kad je X=0....i tako se igraš dok na kraju ne dobiš matricu.... za provjeru, možeš pozbrajati vrijednosti u svakom stupcu i retku, da dobiješ razdiobe od X i Y zasebno
a za ove...ufff...duži su malo, probat ću ti samo jedan objasnit pa se javi ako ne budeš mogla druge...
mislim u 6.39 i 6.40 jedina, kao teža, stvar je računanje ove vjerojatnosti...
6.39.
označimo sa X broj šestica..
zanima nas P(X>50)>0.9
a sada...moramo skužiti kako je X distribuiran...pa kako je to BROJ šestica, očito ima B(n,p)... a kolika je p...pa vjerojatnsot uspjeha i pojedinoj bernulijevo šemi
znači p = 1 - 5^3/6^3 - 3*5^2/6^3.... to je ovo što piše barem 2 šestice...znači 1 - nijedna šestica - jedna šestica..jeli
pa dobro sad kad imamo to je lako dalje
P(X>50) = 1 - P( X<=50) = 1 - fi((50 - np) / sqrt(npq)) a dalje ima već na iljadu mjesta...
6.40...
a skoro pa isto, do na računanje primjerice vjerojatnosti da marko pobjedi ( hint: razdvojiti na disjunktne slučajeve kad marko pobjeđuje, koristit formulu, potpune vjerojatnosti) neznam ak će proć, nisam rješavao ali trebalo bi
a 6.41...
pa imaš rješeno na vježbama nešto slično ali kao sa dve stvari...sad imamo pegaze, jednoroge i konje....
ali vrijednost konja i jednoroga je ista a to je sve što nas zanima...
pa možeš gledat distribuciju na pegaze i nešto.. pri čemu je vjerojatnost od nešto P ( jednorog) + P (konj)....
dalje ko na vježbama
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
mene zanima ak neko zna 6.28, 6.27 i 6.34 ??
za 5.6 a) gledaš napraviš tablicu x * y koja će biti 3 *2 jer X^2 poprima vrijednosti 0 i 1...
a ako gledaš recimo član matrice u kojem je X = 0 a Y=-1 pri čemu je Y= x^2 to je očito nemoguće
ako gledaš da je X=0 Y=0 to je isto onome elementarnom događaju kad je X=0....i tako se igraš dok na kraju ne dobiš matricu.... za provjeru, možeš pozbrajati vrijednosti u svakom stupcu i retku, da dobiješ razdiobe od X i Y zasebno
a za ove...ufff...duži su malo, probat ću ti samo jedan objasnit pa se javi ako ne budeš mogla druge...
mislim u 6.39 i 6.40 jedina, kao teža, stvar je računanje ove vjerojatnosti...
6.39.
označimo sa X broj šestica..
zanima nas P(X>50)>0.9
a sada...moramo skužiti kako je X distribuiran...pa kako je to BROJ šestica, očito ima B(n,p)... a kolika je p...pa vjerojatnsot uspjeha i pojedinoj bernulijevo šemi
znači p = 1 - 5^3/6^3 - 3*5^2/6^3.... to je ovo što piše barem 2 šestice...znači 1 - nijedna šestica - jedna šestica..jeli
pa dobro sad kad imamo to je lako dalje
P(X>50) = 1 - P( X⇐50) = 1 - fi((50 - np) / sqrt(npq)) a dalje ima već na iljadu mjesta...
6.40...
a skoro pa isto, do na računanje primjerice vjerojatnosti da marko pobjedi ( hint: razdvojiti na disjunktne slučajeve kad marko pobjeđuje, koristit formulu, potpune vjerojatnosti) neznam ak će proć, nisam rješavao ali trebalo bi
a 6.41...
pa imaš rješeno na vježbama nešto slično ali kao sa dve stvari...sad imamo pegaze, jednoroge i konje....
ali vrijednost konja i jednoroga je ista a to je sve što nas zanima...
pa možeš gledat distribuciju na pegaze i nešto.. pri čemu je vjerojatnost od nešto P ( jednorog) + P (konj)....
dalje ko na vježbama
Added after 1 minutes:
mene zanima ak neko zna 6.28, 6.27 i 6.34 ??
|
|
| [Vrh] |
|
|















