| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ananas
Forumaš(ica)
Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
Bole13
Forumaš(ica)
Pridružen/a: 01. 11. 2008. (00:33:50)
Postovi: (5A)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)
Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol:
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)
Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol:
|
|
| [Vrh] |
|
pmli
Forumaš(ica)
Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol:
|
|
| [Vrh] |
|
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 21:05 pon, 25. 1. 2010 Naslov: |
    |
|
|
[quote="pbakic"]e da, sad kad su stigli zadaci, jel moze ko rec dal je rijesio zadnji zadatak iz 3. grupe, i kako? (tj kakav polinom se dobije na kraju)[/quote]
sigma1 i sigma2 uvrstiš u treću jednadžbu, imaš polinom s tri nultočke, dakle tri slučaja, a samo jedan zadovoljava onaj uvjet <10
rješenje je x^3 + 2*x^2 - 2 :)
| pbakic (napisa): | | e da, sad kad su stigli zadaci, jel moze ko rec dal je rijesio zadnji zadatak iz 3. grupe, i kako? (tj kakav polinom se dobije na kraju) |
sigma1 i sigma2 uvrstiš u treću jednadžbu, imaš polinom s tri nultočke, dakle tri slučaja, a samo jedan zadovoljava onaj uvjet <10
rješenje je x^3 + 2*x^2 - 2 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)
Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol:
|
| Postano: 21:13 pon, 25. 1. 2010 Naslov: |
|
|
|
[quote="pbakic"]e da, sad kad su stigli zadaci, jel moze ko rec dal je rijesio zadnji zadatak iz 3. grupe, i kako? (tj kakav polinom se dobije na kraju)[/quote]
Možeš i za provjeru utipkati u Wolfram Alphu ovo: Reduce[{s1 == -2, s2 == 2 - s3, s3^3 - 4s3^2 - 22 == -11s2 + 14s1 - 2, s1 s2 s3 < 10}]
(Mislio sam stavit link, al baš i nije uspjelo, pretpostavljam zbog uglatih zagrada... otud kašnjenje :D)
Bez zadnjeg uvijeta su s1 i s2 isti, a s3 je el. {-3, 2, 5}.
Dalje se po Vièteovim formulama lako dobije. Bar mislim, opet sam ih zaboravio, no dobro.
| pbakic (napisa): | | e da, sad kad su stigli zadaci, jel moze ko rec dal je rijesio zadnji zadatak iz 3. grupe, i kako? (tj kakav polinom se dobije na kraju) |
Možeš i za provjeru utipkati u Wolfram Alphu ovo: Reduce[{s1 == -2, s2 == 2 - s3, s3^3 - 4s3^2 - 22 == -11s2 + 14s1 - 2, s1 s2 s3 < 10}]
(Mislio sam stavit link, al baš i nije uspjelo, pretpostavljam zbog uglatih zagrada... otud kašnjenje  )
Bez zadnjeg uvijeta su s1 i s2 isti, a s3 je el. {-3, 2, 5}.
Dalje se po Vièteovim formulama lako dobije. Bar mislim, opet sam ih zaboravio, no dobro.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)
Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol:
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)
Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol:
|
| Postano: 21:39 pon, 25. 1. 2010 Naslov: |
|
|
|
Ne znam, ako se dobro sjećam, kod mene (2. grupa?) su nultočke bile cijeli brojevi. Nisam očekivao ovako nešto, i ako je ovo što su svi dobili točno, ne vjerujem ni da je planirano...
Ne znam, ako se dobro sjećam, kod mene (2. grupa?) su nultočke bile cijeli brojevi. Nisam očekivao ovako nešto, i ako je ovo što su svi dobili točno, ne vjerujem ni da je planirano...
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
anci90
Forumaš(ica)
Pridružen/a: 24. 09. 2009. (14:07:29)
Postovi: (B)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol:
Lokacija: Zd-Zg
|
| Postano: 11:21 uto, 26. 1. 2010 Naslov: |
|
|
|
[quote="pbakic"]ma nije mi bed dobit sigme, nego kad dobijem polinom nemogu mu napiknut nultocku jer nema racionalnih; jedina trojka sigmi koja prodje uvjet su s1=-2, s2=0, s3=2 pa dobijem polinom t^3+2t^2-2[/quote]
sigme koje si dobio su jednake x+ y+ z = -2
xy + yz + xz = 0
xyz = 2.
Ja sam isto krenuo rješavati preko tih jednakosti i dobio sam dvije uređene trojke (x,y,z) (bili su normalni brojevi). Ali su mi svejedno uzeli bod u tom zadatku a nije mi se dalo ići na žalbe :D
Edit: ugl rješava se preko ove 3 nejednakosti, xy kao 2 kroz z pa onda ubacis u drugu pa u prvu (tako nesto san petlja s tim) ...
| pbakic (napisa): | | ma nije mi bed dobit sigme, nego kad dobijem polinom nemogu mu napiknut nultocku jer nema racionalnih; jedina trojka sigmi koja prodje uvjet su s1=-2, s2=0, s3=2 pa dobijem polinom t^3+2t^2-2 |
sigme koje si dobio su jednake x+ y+ z = -2
xy + yz + xz = 0
xyz = 2.
Ja sam isto krenuo rješavati preko tih jednakosti i dobio sam dvije uređene trojke (x,y,z) (bili su normalni brojevi). Ali su mi svejedno uzeli bod u tom zadatku a nije mi se dalo ići na žalbe
Edit: ugl rješava se preko ove 3 nejednakosti, xy kao 2 kroz z pa onda ubacis u drugu pa u prvu (tako nesto san petlja s tim) ...
Zadnja promjena: some_dude; 17:49 uto, 26. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)
Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol:
Lokacija: Somewhere in time
|
| Postano: 12:23 uto, 26. 1. 2010 Naslov: |
|
|
|
[quote="some_dude"][quote="pbakic"]ma nije mi bed dobit sigme, nego kad dobijem polinom nemogu mu napiknut nultocku jer nema racionalnih; jedina trojka sigmi koja prodje uvjet su s1=-2, s2=0, s3=2 pa dobijem polinom t^3+2t^2-2[/quote]
sigme koje si dobio su jednake x+ y+ z = -2
xy + yz + xz = 0
xyz = 2.
Ja sam isto krenuo rješavati preko tih jednakosti i dobio sam dvije uređene trojke (x,y,z) (bili su normalni brojevi). Ali su mi svejedno uzeli bod u tom zadatku a nije mi se dalo ići na žalbe :D[/quote]
prijatelju svaka ti cast,ja bas krenuo bezveze rjesavat taj zadatak i dodem do istoga sto su i svi dobili:
[latex]x+y+z=-2[/latex]
[latex]xy+yz+xz=0[/latex]
[latex]xyz=2[/latex]
odnosno da su rjesenja nultocke od [latex]t^3+2t^2-2[/latex] i kad vidim da tome cudu nultocke nisu ni [latex]\pm 1[/latex], ni [latex]\pm 2[/latex], ja recem svome prijatelju wolframu da mi to rjesi a on ce meni ko iz topa,to ti ima samo jednu nultocku,i to:
[latex]x=-\frac{2}{3}+\frac{1}{3}\sqrt[3]{19-3\sqrt{33}}++\frac{1}{3}\sqrt[3]{19+3\sqrt{33}}[/latex]
...a to mi bas i nije neki normalan broj...
| some_dude (napisa): | | pbakic (napisa): | | ma nije mi bed dobit sigme, nego kad dobijem polinom nemogu mu napiknut nultocku jer nema racionalnih; jedina trojka sigmi koja prodje uvjet su s1=-2, s2=0, s3=2 pa dobijem polinom t^3+2t^2-2 |
sigme koje si dobio su jednake x+ y+ z = -2
xy + yz + xz = 0
xyz = 2.
Ja sam isto krenuo rješavati preko tih jednakosti i dobio sam dvije uređene trojke (x,y,z) (bili su normalni brojevi). Ali su mi svejedno uzeli bod u tom zadatku a nije mi se dalo ići na žalbe |
prijatelju svaka ti cast,ja bas krenuo bezveze rjesavat taj zadatak i dodem do istoga sto su i svi dobili:
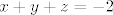
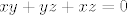
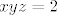
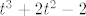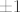odnosno da su rjesenja nultocke od  i kad vidim da tome cudu nultocke nisu ni  , ni 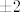 , ja recem svome prijatelju wolframu da mi to rjesi a on ce meni ko iz topa,to ti ima samo jednu nultocku,i to:
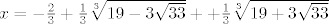
...a to mi bas i nije neki normalan broj...
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja
Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)
Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol:
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
Grga
Forumaš(ica)
Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol:
|
|
| [Vrh] |
|
|
...poanta je u tome sta smo ja i boris u svojim grupama dobili cijele brojeve,a u bakicevoj rjesenje izgleda onako kako izgleda...