| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
dina12
Forumaš(ica)

Pridružen/a: 21. 11. 2009. (17:20:26)
Postovi: (18)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
 Postano: 19:01 uto, 26. 1. 2010 Naslov: Postano: 19:01 uto, 26. 1. 2010 Naslov: |
    |
|
|
Na skupu N x N definiramo relaciju ekvivalencije ? sa (a,b) ? (c,d) ako i samo ako je a+d=b+c. Cijele brojeve možemo definirati kao klase ekvivalencije te relacije. Definirajte zbrajanje takvih klasa [(a,b)]+[(c,d)].
Dokažite da definicija zbrajanja klasa ne ovisi o izboru predstavnika.
Na skupu N x N definiramo relaciju ekvivalencije ? sa (a,b) ? (c,d) ako i samo ako je a+d=b+c. Cijele brojeve možemo definirati kao klase ekvivalencije te relacije. Definirajte zbrajanje takvih klasa [(a,b)]+[(c,d)].
Dokažite da definicija zbrajanja klasa ne ovisi o izboru predstavnika.
Zadnja promjena: gramzon; 22:52 sri, 27. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
biba1804
Forumaš(ica)

Pridružen/a: 27. 01. 2010. (14:34:03)
Postovi: (3)16
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 21:17 sri, 27. 1. 2010 Naslov: Postano: 21:17 sri, 27. 1. 2010 Naslov: |
    |
|
|
[quote="biba1804"]može pomoć oko 5 zadatka? :o
http://web.math.hr/nastava/em/EM1/kolokviji/0910em1kol2.pdf[/quote]
ako sam dobro shvatio,ide ovako:
[latex]\varphi(2^x*7^y)[/latex] po formuli raspisemo kao
[latex]2^x*7^y(1-\frac{1}{2})(1-\frac{1}{7})=84[/latex] i dalje nakon sredivanja,izlucivanja,oduzimanja dobijemo izraz
[latex]2^{x-1}*6*7^{y-1}=84[/latex],ili kad pokratimo [latex]2^{x-1}*7^{y-1}=14[/latex]iz cega je jasno da je jedino rjesenje [latex]x=y=2[/latex]...nisan ni ja ovo zna na kolokviju rjesit,pa u slucaju da je netocno,molio bi nekoga da me ispravi,da ne ispadne da sirim lazi... :lol:
EDIT: kako pretpostavljam da nemas to zapisano u biljeznici,jer bi to inace vidio,mozda ce bit korisno ako ti zapisem teorem ovdje...
[color=blue]Neka je [latex]n=p_1^{\alpha_1}*p_2^{\alpha_2}*...*p_k^{\alpha_k}[/latex] rastav broja n na proste faktore,onda vrijedi:[latex]\varphi(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})[/latex][/color]
ako sam dobro shvatio,ide ovako:
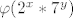 po formuli raspisemo kao po formuli raspisemo kao
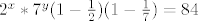 i dalje nakon sredivanja,izlucivanja,oduzimanja dobijemo izraz i dalje nakon sredivanja,izlucivanja,oduzimanja dobijemo izraz
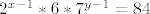 ,ili kad pokratimo ,ili kad pokratimo 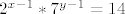 iz cega je jasno da je jedino rjesenje iz cega je jasno da je jedino rjesenje 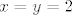 ...nisan ni ja ovo zna na kolokviju rjesit,pa u slucaju da je netocno,molio bi nekoga da me ispravi,da ne ispadne da sirim lazi... ...nisan ni ja ovo zna na kolokviju rjesit,pa u slucaju da je netocno,molio bi nekoga da me ispravi,da ne ispadne da sirim lazi... 
EDIT: kako pretpostavljam da nemas to zapisano u biljeznici,jer bi to inace vidio,mozda ce bit korisno ako ti zapisem teorem ovdje...
Neka je 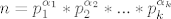 rastav broja n na proste faktore,onda vrijedi: rastav broja n na proste faktore,onda vrijedi: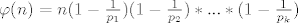
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
Zadnja promjena: jkrstic; 21:49 sri, 27. 1. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 14:48 pet, 29. 1. 2010 Naslov: Postano: 14:48 pet, 29. 1. 2010 Naslov: |
    |
|
|
a nemoj mi nista pricat...pola sata nakon kolokvija san zna rjesit sve osim eventualno dva zadatka,a tamo blokada...nadan se da su mi 4 tocna,jos dva cu uvatit koji bod na tome sta san dosa do pola i jednome san nasa rjesenje,a nisan postupak...kad bi bar ova cetri bila 100 % sigurna,ne bi me bilo stra,al glupo mi je jer mi je ispalo da je onaj sa relacijama i refleksivan i simetrican i antisimetrican i tranzitivan...na pocetku san ga malo pokusa pojednostavnit i dobio nesto posve jednostavno,sad me stra da nisan falio...
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
ok...bojin se da san se sitio toga zadatka i zaboravio san da postoji jos jedan slucaj,ako je ovako izgleda,sto znaci da nisan smio napravit ono sta jesam...
a nemoj mi nista pricat...pola sata nakon kolokvija san zna rjesit sve osim eventualno dva zadatka,a tamo blokada...nadan se da su mi 4 tocna,jos dva cu uvatit koji bod na tome sta san dosa do pola i jednome san nasa rjesenje,a nisan postupak...kad bi bar ova cetri bila 100 % sigurna,ne bi me bilo stra,al glupo mi je jer mi je ispalo da je onaj sa relacijama i refleksivan i simetrican i antisimetrican i tranzitivan...na pocetku san ga malo pokusa pojednostavnit i dobio nesto posve jednostavno,sad me stra da nisan falio...
Added after 5 minutes:
ok...bojin se da san se sitio toga zadatka i zaboravio san da postoji jos jedan slucaj,ako je ovako izgleda,sto znaci da nisan smio napravit ono sta jesam...
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
Sari
Forumaš(ica)

Pridružen/a: 07. 12. 2009. (19:58:14)
Postovi: (11)16
|
|
| [Vrh] |
|
|


















