| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:21 sri, 16. 12. 2009 Naslov: Postano: 20:21 sri, 16. 12. 2009 Naslov: |
    |
|
|
Sve se čini u redu, samo ne znam što misliš pod time da prebacuješ logaritam na desnu stranu. Mislim, možeš, dobit ćeš [latex]\displaystyle 2<-\log_3{(\frac{1}{3}x+11)}[/latex], što je potpuno ista stvar i ne shvaćam kako to mijenja postupak.
Dakle, ja bih rekao da najjednostavniji način rješavanja izgleda ovako. Imam [latex]\displaystyle \log_3{(\frac{1}{3}x+11)}<-2[/latex]. Djelujem potencijom broja [latex]3[/latex] na obje strane (objasnio sam u prethodnom postu zašto to možemo i zašto dobivamo nejednakost ekvivalentnu onoj koju imamo). Dobivam [latex]\displaystyle 3^{\log_3{(\frac{1}{3}x+11)}}<3^{-2}[/latex], tj. kad se logaritam i potencija "pokrate" [latex]\displaystyle \frac{1}{3}x+11<3^{-2}[/latex], što je pojednostavljenje koje smo željeli. (Istodobno zbog uvjeta na definiranost logaritma moramo paziti da vrijedi [latex]0<\frac{1}{3}x+11[/latex], ali to je druga priča.)
Sve se čini u redu, samo ne znam što misliš pod time da prebacuješ logaritam na desnu stranu. Mislim, možeš, dobit ćeš 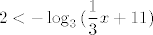 , što je potpuno ista stvar i ne shvaćam kako to mijenja postupak. , što je potpuno ista stvar i ne shvaćam kako to mijenja postupak.
Dakle, ja bih rekao da najjednostavniji način rješavanja izgleda ovako. Imam 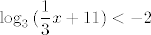 . Djelujem potencijom broja . Djelujem potencijom broja 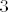 na obje strane (objasnio sam u prethodnom postu zašto to možemo i zašto dobivamo nejednakost ekvivalentnu onoj koju imamo). Dobivam na obje strane (objasnio sam u prethodnom postu zašto to možemo i zašto dobivamo nejednakost ekvivalentnu onoj koju imamo). Dobivam 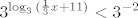 , tj. kad se logaritam i potencija "pokrate" , tj. kad se logaritam i potencija "pokrate" 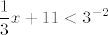 , što je pojednostavljenje koje smo željeli. (Istodobno zbog uvjeta na definiranost logaritma moramo paziti da vrijedi , što je pojednostavljenje koje smo željeli. (Istodobno zbog uvjeta na definiranost logaritma moramo paziti da vrijedi 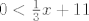 , ali to je druga priča.) , ali to je druga priča.)
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 14:24 uto, 26. 1. 2010 Naslov: Postano: 14:24 uto, 26. 1. 2010 Naslov: |
    |
|
|
Hm...padaju mi na pamet dvije ideje... Ili preko prve derivacije ili ovako nekako...
Znamo da je definicija [latex]sh x = \frac{e^x-e^{-x}}{2}[/latex]. Pogledajmo što nam daje [latex]sh (x+t) - sh x, t>0[/latex]
[latex]sh (x+t) - sh x = \frac{e^{x+t}-e^{-x-t}}{2} - \frac{e^x-e^{-x}}{2} = \frac{e^x \cdot e^t - e^{-x} \cdot e^{-t}-e^x+e^{-x}}{2} =
\frac{e^x \cdot (e^t-1) - e^{-x} \cdot (e^{-t}-1)}{2} = \\
= \frac{e^x \cdot (e^t-1) - e^{-x} (\frac{1}{e^t}-1)}{2}
= \frac{e^x \cdot (e^t-1) - e^{-x} \cdot \frac{1-e^t}{e^t}}{2}
= \frac{\frac{e^t \cdot e^x \cdot (e^t-1) + e^{-x} \cdot (e^t-1)}{e^t}}{2} = \\
= \frac{(e^t-1)(e^{x+t}+e^{-x})}{2e^t}[/latex]
Rezultat je pozitivan [latex]\forall x \in \mathbb{R}, \forall t \in \mathbb{R}^+[/latex], pa je to potvrđuje da je funkcija strogo rastuća funkcija... Dvojbena je bila jedino ova prva zagrada, ali ona je pozitivna za svaki t>0, a negativna za svaki t<0.
Ovo je rješenje koristeći prvu derivaciju...budem si to sada raspisao, pa zakeljim tu...
Analogno možeš napraviti i za ch...
[size=9][color=#999999]Added after 7 minutes:[/color][/size]
Rješenje pomoćuprve derivacije...
[latex](sh x)' = ch x[/latex].
Ch je pozitivna za svaki x (vidi se iz same definicije ch), pa je sh x rastuća na cijeloj domeni.
Hm...padaju mi na pamet dvije ideje... Ili preko prve derivacije ili ovako nekako...
Znamo da je definicija 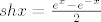 . Pogledajmo što nam daje . Pogledajmo što nam daje 

Rezultat je pozitivan 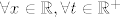 , pa je to potvrđuje da je funkcija strogo rastuća funkcija... Dvojbena je bila jedino ova prva zagrada, ali ona je pozitivna za svaki t>0, a negativna za svaki t<0. , pa je to potvrđuje da je funkcija strogo rastuća funkcija... Dvojbena je bila jedino ova prva zagrada, ali ona je pozitivna za svaki t>0, a negativna za svaki t<0.
Ovo je rješenje koristeći prvu derivaciju...budem si to sada raspisao, pa zakeljim tu...
Analogno možeš napraviti i za ch...
Added after 7 minutes:
Rješenje pomoćuprve derivacije...
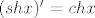 . .
Ch je pozitivna za svaki x (vidi se iz same definicije ch), pa je sh x rastuća na cijeloj domeni.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
surosev
Forumaš(ica)
Pridružen/a: 20. 01. 2010. (20:08:09)
Postovi: (9)16
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 22:28 uto, 26. 1. 2010 Naslov: Postano: 22:28 uto, 26. 1. 2010 Naslov: |
    |
|
|
[quote="surosev"]Puno jednostavnije: funkcija e^x je strogo rasuća funkcija. Funkcija e^-x je strogo padajuća pa je zbog toga funkcija -e^-x stogo rasuća. shx=1/2e^x-1/2e^-x što znači shx je linearna kombinacija strogo rastućih funkcija te je time i ona strogo rastuća funkcija. Naravno, potrebno je napisati te sve dokaze (koji nisu dugi i čovjek se u njima snađe puno lakše nego u gornjem, a derivacije još k tome nismo niti učili). :wink:
Ako ima problema sa dokazivanjem, slobodno pitaj, nije mi ih se dalo pisati jer ih imaš u bilježnici (pod uvjetom da si išao na predavanja). :)[/quote]
Hvala, to nam je prof. Šikić zadao da doma dokažemo, pa sam sad kad učim naišao na to. Znaći trebam dokazati e^x str. rastuća i -e^-x str rastuća. Trebam li i dokazati da je linearna kombinacija rastućih funkcija rastuća ili se to podrazumjeva?
| surosev (napisa): | Puno jednostavnije: funkcija e^x je strogo rasuća funkcija. Funkcija e^-x je strogo padajuća pa je zbog toga funkcija -e^-x stogo rasuća. shx=1/2e^x-1/2e^-x što znači shx je linearna kombinacija strogo rastućih funkcija te je time i ona strogo rastuća funkcija. Naravno, potrebno je napisati te sve dokaze (koji nisu dugi i čovjek se u njima snađe puno lakše nego u gornjem, a derivacije još k tome nismo niti učili). 
Ako ima problema sa dokazivanjem, slobodno pitaj, nije mi ih se dalo pisati jer ih imaš u bilježnici (pod uvjetom da si išao na predavanja).  |
Hvala, to nam je prof. Šikić zadao da doma dokažemo, pa sam sad kad učim naišao na to. Znaći trebam dokazati e^x str. rastuća i -e^-x str rastuća. Trebam li i dokazati da je linearna kombinacija rastućih funkcija rastuća ili se to podrazumjeva?
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 22:56 uto, 26. 1. 2010 Naslov: Postano: 22:56 uto, 26. 1. 2010 Naslov: |
    |
|
|
[quote="Tomy007"][quote="surosev"]Puno jednostavnije: funkcija e^x je strogo rasuća funkcija. Funkcija e^-x je strogo padajuća pa je zbog toga funkcija -e^-x stogo rasuća. shx=1/2e^x-1/2e^-x što znači shx je linearna kombinacija strogo rastućih funkcija te je time i ona strogo rastuća funkcija. Naravno, potrebno je napisati te sve dokaze (koji nisu dugi i čovjek se u njima snađe puno lakše nego u gornjem, a derivacije još k tome nismo niti učili). :wink:
Ako ima problema sa dokazivanjem, slobodno pitaj, nije mi ih se dalo pisati jer ih imaš u bilježnici (pod uvjetom da si išao na predavanja). :)[/quote]
Hvala, to nam je prof. Šikić zadao da doma dokažemo, pa sam sad kad učim naišao na to. Znaći trebam dokazati e^x str. rastuća i -e^-x str rastuća. Trebam li i dokazati da je linearna kombinacija rastućih funkcija rastuća ili se to podrazumjeva?[/quote]
Ako su f i g rastuce, i a,b >0 tada:
[latex]x > y \Rightarrow f(x) \geq f(y) \Rightarrow a\cdot f(x) \geq a \cdot f(y)[/latex]
[latex]x > y \Rightarrow g(x) \geq g(y) \Rightarrow b\cdot g(x) \geq b \cdot g(y)[/latex]
Ocito tada vrijedi i
[latex]x > y \Rightarrow a\cdot f(x)+b\cdot g(x) \geq a \cdot f(y)+b \cdot g(y)[/latex]
Znaci nije bas linearna kombinacija jer nece vrijediti opcenito ako nisu i a i b veci od 0, ali dokle god su oba broja veca, onda vrijedi tvrdnja i mislim da mozes uzeti da se to podrazumijeva (a ako se trazi da dokazes prilicno je jednostavno)
| Tomy007 (napisa): | | surosev (napisa): | Puno jednostavnije: funkcija e^x je strogo rasuća funkcija. Funkcija e^-x je strogo padajuća pa je zbog toga funkcija -e^-x stogo rasuća. shx=1/2e^x-1/2e^-x što znači shx je linearna kombinacija strogo rastućih funkcija te je time i ona strogo rastuća funkcija. Naravno, potrebno je napisati te sve dokaze (koji nisu dugi i čovjek se u njima snađe puno lakše nego u gornjem, a derivacije još k tome nismo niti učili). 
Ako ima problema sa dokazivanjem, slobodno pitaj, nije mi ih se dalo pisati jer ih imaš u bilježnici (pod uvjetom da si išao na predavanja).  |
Hvala, to nam je prof. Šikić zadao da doma dokažemo, pa sam sad kad učim naišao na to. Znaći trebam dokazati e^x str. rastuća i -e^-x str rastuća. Trebam li i dokazati da je linearna kombinacija rastućih funkcija rastuća ili se to podrazumjeva? |
Ako su f i g rastuce, i a,b >0 tada:
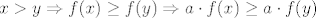
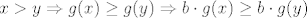
Ocito tada vrijedi i
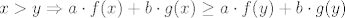
Znaci nije bas linearna kombinacija jer nece vrijediti opcenito ako nisu i a i b veci od 0, ali dokle god su oba broja veca, onda vrijedi tvrdnja i mislim da mozes uzeti da se to podrazumijeva (a ako se trazi da dokazes prilicno je jednostavno)
_________________
Bri
|
|
| [Vrh] |
|
surosev
Forumaš(ica)
Pridružen/a: 20. 01. 2010. (20:08:09)
Postovi: (9)16
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
dodomagio
Forumaš(ica)

Pridružen/a: 07. 02. 2010. (16:13:06)
Postovi: (3)16
|
 Postano: 16:30 ned, 7. 2. 2010 Naslov: Postano: 16:30 ned, 7. 2. 2010 Naslov: |
    |
|
|
Pozdrav,
Iako nisam student PMF-a tražim vašu pomoć oko jednog zadatka ...
Ovako, nađite domenu, skup vrijednosti, ispitajte rubno ponašanje, napravite tablicu predznaka, tablicu rasta, pada i ekstrema (odredite globalne ekstreme) te tablicu zakretanja i točka pregiba. I riješite jednadžbu f(x)=0 i f(x)>0
Sve bi to nekako i riješio kada bi imao zadanu funkciju jednadžbom (jer sve upute sam našao kako se to radi međutim funkcija je zadana grafom.
Pozdrav,
Iako nisam student PMF-a tražim vašu pomoć oko jednog zadatka ...
Ovako, nađite domenu, skup vrijednosti, ispitajte rubno ponašanje, napravite tablicu predznaka, tablicu rasta, pada i ekstrema (odredite globalne ekstreme) te tablicu zakretanja i točka pregiba. I riješite jednadžbu f(x)=0 i f(x)>0
Sve bi to nekako i riješio kada bi imao zadanu funkciju jednadžbom (jer sve upute sam našao kako se to radi međutim funkcija je zadana grafom.
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
 Postano: 18:43 ned, 7. 2. 2010 Naslov: Postano: 18:43 ned, 7. 2. 2010 Naslov: |
    |
|
|
[quote="dodomagio"]Pozdrav,
Iako nisam student PMF-a tražim vašu pomoć oko jednog zadatka ...
Ovako, nađite domenu, skup vrijednosti, ispitajte rubno ponašanje, napravite tablicu predznaka, tablicu rasta, pada i ekstrema (odredite globalne ekstreme) te tablicu zakretanja i točka pregiba. I riješite jednadžbu f(x)=0 i f(x)>0
Sve bi to nekako i riješio kada bi imao zadanu funkciju jednadžbom (jer sve upute sam našao kako se to radi međutim funkcija je zadana grafom.[/quote]
ali nisam sigurna jel se ono graf prekida u x=4 ili je os apscisa horizontalna asimptota;
u prvom slucaju mislim da je domena ocita: <-besk.,4] \{-3}, isto tako i u drugom : R\{-3}
Sto se tice skipa vrijednosti, takoder je vidljivo sa slike:
tj Imf= [-2, + besk>
f(x)=0...takoder vidljivo sa grafa: -2
f(x)>0 za tj za x e [-4,-2]\{-3} i ako je nacrtano u mjerilo trebalo bi biti i x e<-besk.,-5]
ekstremi: globalni minimum iscitavamo da je -2 a globalnog max nemamo
tablice je isto tako naprave tako da se cita sa grafa
| dodomagio (napisa): | Pozdrav,
Iako nisam student PMF-a tražim vašu pomoć oko jednog zadatka ...
Ovako, nađite domenu, skup vrijednosti, ispitajte rubno ponašanje, napravite tablicu predznaka, tablicu rasta, pada i ekstrema (odredite globalne ekstreme) te tablicu zakretanja i točka pregiba. I riješite jednadžbu f(x)=0 i f(x)>0
Sve bi to nekako i riješio kada bi imao zadanu funkciju jednadžbom (jer sve upute sam našao kako se to radi međutim funkcija je zadana grafom. |
ali nisam sigurna jel se ono graf prekida u x=4 ili je os apscisa horizontalna asimptota;
u prvom slucaju mislim da je domena ocita: ←besk.,4] \{-3}, isto tako i u drugom : R\{-3}
Sto se tice skipa vrijednosti, takoder je vidljivo sa slike:
tj Imf= [-2, + besk>
f(x)=0...takoder vidljivo sa grafa: -2
f(x)>0 za tj za x e [-4,-2]\{-3} i ako je nacrtano u mjerilo trebalo bi biti i x e←besk.,-5]
ekstremi: globalni minimum iscitavamo da je -2 a globalnog max nemamo
tablice je isto tako naprave tako da se cita sa grafa
_________________
Give me a place to stand, and I will move the earth.
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 12:17 uto, 9. 2. 2010 Naslov: Postano: 12:17 uto, 9. 2. 2010 Naslov: |
    |
|
|
ovak....
vidis na grafu ak uzmes bilo koji x sa x - osi mozes mu naci y na y -osi takav da je f( x ) = y osim u tocki x = -3, ( mozes gledati sve okomice na x -os i vidjet ces da ce svaka sjec graf u nekoj tocki osim okomice x = -3 ), pa je domena R\{ -3 }. Vidis da graf ima svoj minimum u tocki y = -2, a supremuma( maximuma ) nema pa ce ako uzmes bilo koji x iz domene f( x ) ce biti iz skupa [2,+beskonacno>, pa je to skup vrijednosti koje funkcija postize, kada x -> +beskonaco onda vidis da se f( x ) sve vise i vise priblizava 0, a kada x -> -beskonacno vidis da f( x ) ide prema +beskonacno ( rubno ponasanje ), tablicu predznaka napravis tak da gledas za koje x -eve je f( x ) > 0 a za koje f( x ) < 0. Dobijes da je:
f( x ) > 0 za x iz <-beskonano, -5>U<-4,-3>U<-3,-2> i
f( x ) < 0 za x iz <-5,-4>U<-2, +beskonano >
Za tablicu rasta gledas za koje x- eve funkcija pada a za koje raste ( na slici funkcija pada za one x -eve za koje krivulja ide od 2. prema 4.kvadrantu, a raste za one za koje krivulja ide od 3. prema 1. kvadrantu )
sve ostalo vidis isto iz grafa ( ekstreme i gdje je f( x ) = 0 ( 3 tocke ), a gdje je f( x ) > 0 vidis iz tablice za predznak )
ovak....
vidis na grafu ak uzmes bilo koji x sa x - osi mozes mu naci y na y -osi takav da je f( x ) = y osim u tocki x = -3, ( mozes gledati sve okomice na x -os i vidjet ces da ce svaka sjec graf u nekoj tocki osim okomice x = -3 ), pa je domena R\{ -3 }. Vidis da graf ima svoj minimum u tocki y = -2, a supremuma( maximuma ) nema pa ce ako uzmes bilo koji x iz domene f( x ) ce biti iz skupa [2,+beskonacno>, pa je to skup vrijednosti koje funkcija postize, kada x -> +beskonaco onda vidis da se f( x ) sve vise i vise priblizava 0, a kada x -> -beskonacno vidis da f( x ) ide prema +beskonacno ( rubno ponasanje ), tablicu predznaka napravis tak da gledas za koje x -eve je f( x ) > 0 a za koje f( x ) < 0. Dobijes da je:
f( x ) > 0 za x iz <-beskonano, -5>U<-4,-3>U<-3,-2> i
f( x ) < 0 za x iz <-5,-4>U<-2, +beskonano >
Za tablicu rasta gledas za koje x- eve funkcija pada a za koje raste ( na slici funkcija pada za one x -eve za koje krivulja ide od 2. prema 4.kvadrantu, a raste za one za koje krivulja ide od 3. prema 1. kvadrantu )
sve ostalo vidis isto iz grafa ( ekstreme i gdje je f( x ) = 0 ( 3 tocke ), a gdje je f( x ) > 0 vidis iz tablice za predznak )
|
|
| [Vrh] |
|
dodomagio
Forumaš(ica)

Pridružen/a: 07. 02. 2010. (16:13:06)
Postovi: (3)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 16:16 sri, 10. 2. 2010 Naslov: Postano: 16:16 sri, 10. 2. 2010 Naslov: |
    |
|
|
s obzirom da nemamo jednadzbu funkcije nego samo sliku mi ne mozemo znati kako ce se ona ponasati izvan slike, pa sada s obzirom da mi vidimo samo jedan mali dio grafa mi mozemo na tom malom dijelu i odrediti domenu, ali izvan tog dijela ne, ta funkcija se moze bilo kako ponasati na djelu kojeg ne vidimo, pa u biti ti i ne mozes sa 100% -tnom sigurnošču reći da je to domena ( R\{ -3 } u ovom slucaju ), međutim mozes pretpostaviti, jer mozes pretpostaviti da na onom djelu koji ne vidis funkcija ce se ponasati onako kako se ponasa na rubovima tvoje slike, jer da to ne pretpostavis ne bi mogao dati odgovor na pitanje koja je domena funkcije f.
Pa pretpostavljam da ce vrijednosti funkcije rasti kada ide u - beskonacno, a priblizavati se 0 kada ide u +beskonacno. Inace određivanje domene preko grafa ne bi imalo smisla
s obzirom da nemamo jednadzbu funkcije nego samo sliku mi ne mozemo znati kako ce se ona ponasati izvan slike, pa sada s obzirom da mi vidimo samo jedan mali dio grafa mi mozemo na tom malom dijelu i odrediti domenu, ali izvan tog dijela ne, ta funkcija se moze bilo kako ponasati na djelu kojeg ne vidimo, pa u biti ti i ne mozes sa 100% -tnom sigurnošču reći da je to domena ( R\{ -3 } u ovom slucaju ), međutim mozes pretpostaviti, jer mozes pretpostaviti da na onom djelu koji ne vidis funkcija ce se ponasati onako kako se ponasa na rubovima tvoje slike, jer da to ne pretpostavis ne bi mogao dati odgovor na pitanje koja je domena funkcije f.
Pa pretpostavljam da ce vrijednosti funkcije rasti kada ide u - beskonacno, a priblizavati se 0 kada ide u +beskonacno. Inace određivanje domene preko grafa ne bi imalo smisla
|
|
| [Vrh] |
|
dodomagio
Forumaš(ica)

Pridružen/a: 07. 02. 2010. (16:13:06)
Postovi: (3)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 20:01 sub, 27. 2. 2010 Naslov: Postano: 20:01 sub, 27. 2. 2010 Naslov: |
    |
|
|
Bok Ljudi!
Imam jedno pitanjce u svezi domena funkcije.
Imam ovdje jedan zadatak sa rjesenjem koji sam skuzio, ali na kraju dobiveni rezultat ne kuzim, pa ako moze objasnjenje kako je dobiven rezultat.
Ovako treba odrediti domenu funkcije:
[latex]\frac{3-2x}{5x+2} > 0[/latex]
[latex]Rjesenje 1. nejednadzbe je \langle \frac{-2}{5},\frac{3}{2} \rangle [/latex]
[latex]Rjesenje 2.nejednadzbe R(2.)=R(A) \cup R(B) = \langle -\infty, \frac{-2}{5} \rangle \cup [\frac{-7}{27}, + \infty \rangle
[/latex]
[latex]Ukupno rjesenje je :
D = R (1.)\cap R(2.) = \langle \frac{-2}{5} ,\frac{3}{2}\rangle \cap (\langle -\infty,\frac{-2}{5}\rangle \cup [ \frac{-7}{27}, + \infty \rangle )[/latex]
[latex]E sad kako je dobiven krajnji rezultat [ \frac{-7}{27}, \frac{3}{2}][/latex]
[latex]Zasto je tj.zbog kojeg razloga uzet \frac{-7}{27} ? i \frac{3}{2} ? [/latex]
Ako moze objasnjenje ( nadam se da sam jasno obrazlozio sta me zulja u zadatku :D
Hvala unaprijed
Bok Ljudi!
Imam jedno pitanjce u svezi domena funkcije.
Imam ovdje jedan zadatak sa rjesenjem koji sam skuzio, ali na kraju dobiveni rezultat ne kuzim, pa ako moze objasnjenje kako je dobiven rezultat.
Ovako treba odrediti domenu funkcije:
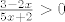
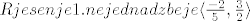
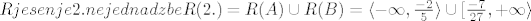
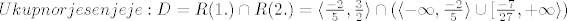
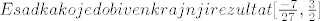
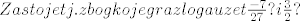
Ako moze objasnjenje ( nadam se da sam jasno obrazlozio sta me zulja u zadatku 
Hvala unaprijed
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 20:42 sub, 27. 2. 2010 Naslov: Postano: 20:42 sub, 27. 2. 2010 Naslov: |
    |
|
|
Krajnji rezultat je dobiven presjekom rješenja posebnih slučajeva. Nacrtaj si to ovako: nacrtaj si brojevni pravac. Rješenje prvog slučaja iscrtkaj crticama...npr, ovakvim crticama --> \\\\\. Rješenje drugog slučaja iscrtkaj ovakvim crticama -----> /////. Tamo gdje ti se poklapaju crtice prvog i drugog slučaja je presjek...odnosno konačno rješenje...
Što je ustvari presjek dvaju skupova? To je novi skup u koji utrpamo sve one koji su i u prvom i drugom skupu.
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
Btw, zadatk je krivo rješen...
Ajmo pokušati ovako... Prvo ćemo odrediti nultočku funkcije [latex]y_1 = 3-2x[/latex]. To je točka [latex]x = \frac{3}{2}[/latex]. Odredimo zatim nultočku funkcije [latex]y_2 = 5x+2[/latex]. To je točka [latex]x = -\frac{2}{5}[/latex].
Zatim primjeti da je prva funkcija (ona koje je u brojniku) padajuća (koeficijent smjera je negativan!)...odnosno - do nultočke će imati pozitivne vrijednosti, a nakon nultočke negativne.
Za razliku od druge funkcije koja je rastuća (koeficijent smjera je pozitivan)...odnosno - do nultočke će imati negativne vrijednosti, a nakon nultočke pozitivne.
Nacrtaj sada brojevni pravac i obilježi nultočke 1. i 2. funkcije. Time si brojevni pravac podijelio na tri dijela...
1. dio je [latex]<-\infty, -\frac{2}{5}>[/latex]. U ovom je intervalu 1. funkcija pozitivna, a druga negativna... A znamo još iz šestog razreda osnovne škole (+):(-) = (-)... A nama se traži kad je pozitivno, pa idemo dalje.
2. dio je [latex]<-\frac{2}{5}, \frac{3}{2}>[/latex]. U ovom je intervalu 1. funkcija pozitivna, druga je također pozitivna. Znamo da (+):(+) = (+)... Nama se upravo to traži, pa si obilježimo to kao rješenje.
3- dio je [latex]<\frac{3}{2}, \infty>[/latex]. U ovom je intervalu 1. funkcija negativna, druga je pozitivna. Znamo da je (-):(+) = (-), što nama ne odgovara...
Dakle, konačno rješenje je: [latex]x\in <-\frac{2}{5}, \frac{3}{2}>[/latex].
Btw, molim te provjeri sve ovo jer sam rješavao bez papira, pa postoji mogućnost pogreške.
Krajnji rezultat je dobiven presjekom rješenja posebnih slučajeva. Nacrtaj si to ovako: nacrtaj si brojevni pravac. Rješenje prvog slučaja iscrtkaj crticama...npr, ovakvim crticama → \\\\\. Rješenje drugog slučaja iscrtkaj ovakvim crticama -----> /////. Tamo gdje ti se poklapaju crtice prvog i drugog slučaja je presjek...odnosno konačno rješenje...
Što je ustvari presjek dvaju skupova? To je novi skup u koji utrpamo sve one koji su i u prvom i drugom skupu.
Added after 11 minutes:
Btw, zadatk je krivo rješen...
Ajmo pokušati ovako... Prvo ćemo odrediti nultočku funkcije 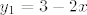 . To je točka . To je točka  . Odredimo zatim nultočku funkcije . Odredimo zatim nultočku funkcije 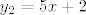 . To je točka . To je točka 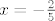 . .
Zatim primjeti da je prva funkcija (ona koje je u brojniku) padajuća (koeficijent smjera je negativan!)...odnosno - do nultočke će imati pozitivne vrijednosti, a nakon nultočke negativne.
Za razliku od druge funkcije koja je rastuća (koeficijent smjera je pozitivan)...odnosno - do nultočke će imati negativne vrijednosti, a nakon nultočke pozitivne.
Nacrtaj sada brojevni pravac i obilježi nultočke 1. i 2. funkcije. Time si brojevni pravac podijelio na tri dijela...
1. dio je 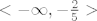 . U ovom je intervalu 1. funkcija pozitivna, a druga negativna... A znamo još iz šestog razreda osnovne škole (+) . U ovom je intervalu 1. funkcija pozitivna, a druga negativna... A znamo još iz šestog razreda osnovne škole (+) -) = (-)... A nama se traži kad je pozitivno, pa idemo dalje. -) = (-)... A nama se traži kad je pozitivno, pa idemo dalje.
2. dio je 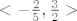 . U ovom je intervalu 1. funkcija pozitivna, druga je također pozitivna. Znamo da (+) . U ovom je intervalu 1. funkcija pozitivna, druga je također pozitivna. Znamo da (+) +) = (+)... Nama se upravo to traži, pa si obilježimo to kao rješenje. +) = (+)... Nama se upravo to traži, pa si obilježimo to kao rješenje.
3- dio je 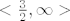 . U ovom je intervalu 1. funkcija negativna, druga je pozitivna. Znamo da je (-) . U ovom je intervalu 1. funkcija negativna, druga je pozitivna. Znamo da je (-) +) = (-), što nama ne odgovara... +) = (-), što nama ne odgovara...
Dakle, konačno rješenje je: 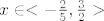 . .
Btw, molim te provjeri sve ovo jer sam rješavao bez papira, pa postoji mogućnost pogreške.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
|











