| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 9:37 ned, 28. 2. 2010 Naslov: Postano: 9:37 ned, 28. 2. 2010 Naslov: |
    |
|
|
Dakle, razmisli koji bi ti sve dijelovi mogli stvarati probleme. Prvo, [latex]5x+2[/latex] mora biti različito od [latex]0[/latex] (jer je to nazivnik). Nadalje, [latex]\displaystyle\frac{3-2x}{5x+2}[/latex] mora biti veće od [latex]0[/latex] (jer je logaritam definiran samo na brojevima većima od [latex]0[/latex]). Naposlijetku, izraz pod korijenom ne smije biti manji od [latex]0[/latex], pa mora vrijediti [latex]\displaystyle\log_5{\frac{3-2x}{5x+2}}\leq 1[/latex], tj. [latex]\displaystyle\frac{3-2x}{5x+2}\leq 5[/latex].
Sad, kad smo vidjeli sve uvjete, uzimanjem presjeka (jer moraju vrijediti svi slučajevi) vidimo da su nam rješenje svi [latex]x[/latex] takvi da je [latex]\displaystyle 0<\frac{3-2x}{5x+2}\leq 5[/latex], a to nije neki problem riješiti - možemo recimo uzeti dva slučaja: u prvom je [latex]5x+2>0[/latex] i tada imamo [latex]0<3-2x\leq 25x+10[/latex], tj. [latex]\displaystyle x\in\[-\frac{7}{27},\frac{3}{2}\rangle[/latex]. Zapravo, morali bismo i paziti da za sve te [latex]x[/latex] zaista vrijedi [latex]5x+2>0[/latex], ali to je u ovom slučaju očito budući da je [latex]\displaystyle -\frac{7}{27}\geq -\frac{2}{5}[/latex].
Drugi slučaj je [latex]5x+2<0[/latex], no tada lako vidimo (možemo i ići istim postupkom kao gore) da nema rješenja - naime, morali bismo imati i [latex]3-2x<0[/latex], tj. [latex]\displaystyle -\frac{2}{5}>x>\frac{3}{2}[/latex], što je očita kontradikcija.
Dakle, finalno rješenje (koje dobivamo unijom ova dva slučaja, od kojih drugi zapravo nema rješenja) je [latex]\displaystyle\[-\frac{7}{27},\frac{3}{2}\rangle[/latex].
Dakle, razmisli koji bi ti sve dijelovi mogli stvarati probleme. Prvo, 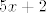 mora biti različito od mora biti različito od  (jer je to nazivnik). Nadalje, (jer je to nazivnik). Nadalje, 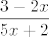 mora biti veće od mora biti veće od  (jer je logaritam definiran samo na brojevima većima od (jer je logaritam definiran samo na brojevima većima od  ). Naposlijetku, izraz pod korijenom ne smije biti manji od ). Naposlijetku, izraz pod korijenom ne smije biti manji od  , pa mora vrijediti , pa mora vrijediti 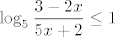 , tj. , tj. 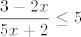 . .
Sad, kad smo vidjeli sve uvjete, uzimanjem presjeka (jer moraju vrijediti svi slučajevi) vidimo da su nam rješenje svi  takvi da je takvi da je 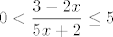 , a to nije neki problem riješiti - možemo recimo uzeti dva slučaja: u prvom je , a to nije neki problem riješiti - možemo recimo uzeti dva slučaja: u prvom je 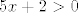 i tada imamo i tada imamo 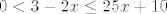 , tj. , tj. 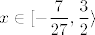 . Zapravo, morali bismo i paziti da za sve te . Zapravo, morali bismo i paziti da za sve te  zaista vrijedi zaista vrijedi 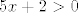 , ali to je u ovom slučaju očito budući da je , ali to je u ovom slučaju očito budući da je 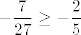 . .
Drugi slučaj je 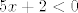 , no tada lako vidimo (možemo i ići istim postupkom kao gore) da nema rješenja - naime, morali bismo imati i , no tada lako vidimo (možemo i ići istim postupkom kao gore) da nema rješenja - naime, morali bismo imati i 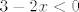 , tj. , tj. 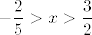 , što je očita kontradikcija. , što je očita kontradikcija.
Dakle, finalno rješenje (koje dobivamo unijom ova dva slučaja, od kojih drugi zapravo nema rješenja) je 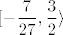 . .
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 10:21 ned, 28. 2. 2010 Naslov: Postano: 10:21 ned, 28. 2. 2010 Naslov: |
    |
|
|
Je ,mornik puno hvala!!
Jos me nesto malo zbunjuje ; te zagrade, nekad su obicne ,nekad uglate...
kako se odreduje koja zagrade dolazi na koje mjesto, tu mora biti neko pravilo ,posto nam je profesorica na proslom ispitu zbog krivih zagrada oduzimala bodove :(
npr.[latex]\displaystyle[-\frac{7}{27},\frac{3}{2}\rangle[/latex]
zasto su tu ove dvije ,a ne neke druge ,npr.iste dvije zagrade?
Je ,mornik puno hvala!!
Jos me nesto malo zbunjuje ; te zagrade, nekad su obicne ,nekad uglate...
kako se odreduje koja zagrade dolazi na koje mjesto, tu mora biti neko pravilo ,posto nam je profesorica na proslom ispitu zbog krivih zagrada oduzimala bodove 
npr.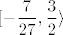
zasto su tu ove dvije ,a ne neke druge ,npr.iste dvije zagrade?
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 11:22 pon, 1. 3. 2010 Naslov: Postano: 11:22 pon, 1. 3. 2010 Naslov: |
    |
|
|
Ne znam, trebalo bi imati smisla na brojevnom pravcu, samo moraš paziti što znači unija, a što presjek. :? No dobro, hajde da probamo to riječima objasniti. :)
Dakle, tebe (zbog presjeka) zanimaju svi brojevi koji su u prvom uvjetu ([latex]\displaystyle \langle\frac{7}{5},\frac{3}{2}\rangle[/latex]) i u drugom uvjetu ([latex]\displaystyle \langle -\infty,\frac{10}{7}\rangle \cup \langle \frac{3}{2},+\infty\rangle[/latex]).
Stoga, tebe zanimaju svi [latex]x[/latex] koji zadovoljavaju [latex]\displaystyle \frac{7}{5}<x<\frac{3}{2}[/latex] i barem jedno od sljedećeg: [latex]\displaystyle x\leq\frac{10}{7}[/latex], [latex]\displaystyle x>\frac{3}{2}[/latex].
Sad primijeti da je očito nemoguće postići da vrijedi [latex]\displaystyle \frac{7}{5}<x<\frac{3}{2}[/latex] i [latex]\displaystyle x>\frac{3}{2}[/latex]. Stoga, budući da mora vrijediti barem jedna od one dvije nejednakosti, mora vrijediti [latex]\displaystyle x\leq\frac{10}{7}[/latex] (i, naravno, [latex]\displaystyle \frac{7}{5}<x<\frac{3}{2}[/latex]).
Sad samo pogledaj što smo dobili: [latex]x[/latex] mora biti manje ili jednako od [latex]\displaystyle \frac{10}{7}[/latex] i manje od [latex]\displaystyle \frac{3}{2}[/latex]. Kako je [latex]\displaystyle \frac{10}{7}<\frac{3}{2}[/latex], za ovaj dio nam je nužno i dovoljno [latex]\displaystyle x\leq \frac{10}{7}[/latex]. S druge strane, imamo i ograničenje odozdo: [latex]\displaystyle \frac{7}{5}<x[/latex].
Dakle, rješenje su svi brojevi [latex]x[/latex] takvi da [latex]\displaystyle \frac{7}{5}<x\leq\frac{10}{7}[/latex], a oni upravo čine interval [latex]\displaystyle\langle\frac{7}{5},\frac{10}{7}\][/latex].
Ne znam, trebalo bi imati smisla na brojevnom pravcu, samo moraš paziti što znači unija, a što presjek.  No dobro, hajde da probamo to riječima objasniti. No dobro, hajde da probamo to riječima objasniti. 
Dakle, tebe (zbog presjeka) zanimaju svi brojevi koji su u prvom uvjetu (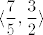 ) i u drugom uvjetu ( ) i u drugom uvjetu (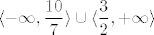 ). ).
Stoga, tebe zanimaju svi  koji zadovoljavaju koji zadovoljavaju 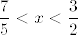 i barem jedno od sljedećeg: i barem jedno od sljedećeg: 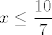 , , 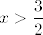 . .
Sad primijeti da je očito nemoguće postići da vrijedi 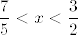 i i 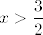 . Stoga, budući da mora vrijediti barem jedna od one dvije nejednakosti, mora vrijediti . Stoga, budući da mora vrijediti barem jedna od one dvije nejednakosti, mora vrijediti 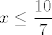 (i, naravno, (i, naravno, 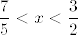 ). ).
Sad samo pogledaj što smo dobili:  mora biti manje ili jednako od mora biti manje ili jednako od 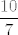 i manje od i manje od  . Kako je . Kako je 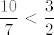 , za ovaj dio nam je nužno i dovoljno , za ovaj dio nam je nužno i dovoljno 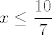 . S druge strane, imamo i ograničenje odozdo: . S druge strane, imamo i ograničenje odozdo: 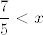 . .
Dakle, rješenje su svi brojevi  takvi da takvi da 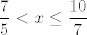 , a oni upravo čine interval , a oni upravo čine interval 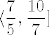 . .
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:31 pon, 1. 3. 2010 Naslov: Postano: 12:31 pon, 1. 3. 2010 Naslov: |
    |
|
|
Sviđa mi se što zadatak nazivaš situacijom i taj ću izraz svakako pokrasti :lol: , ali i dalje baš ne vidim jesam li dobro shvatio zadatak. Naime, [latex]2[/latex] je svakako u intervalu koji si napisao, ali [latex]\displaystyle\log_{1/2}\frac{2-1}{3-2\cdot 2}[/latex] nije uopće definiran. Naime, [latex]\displaystyle \frac{2-1}{3-2\cdot 2}=-1\leq 0[/latex].
Naprotiv, domena je [latex]\displaystyle\langle 1,\frac{3}{2}\rangle[/latex] - relativno se lako vidi da je tada i samo tada [latex]\displaystyle \frac{x-1}{3-2x}>0[/latex], što nam je potrebno. Mislim da je skup rješenja [latex]\displaystyle\langle 1,\frac{7}{6}\][/latex], ali to baš i nisam pretjerano provjeravao - u svakom slučaju, račun sam po sebi ne bi trebao biti težak - zanima te kad je [latex]\displaystyle 0<\frac{x-1}{3-2x}<\frac{1}{4}[/latex]. :)
Sad ne znam, možda sam ja nešto zaznuo, možda tu fale neke zagrade, štoli, ali, sve u svemu, trenutno ni ja to ne mogu objasniti. :)
Sviđa mi se što zadatak nazivaš situacijom i taj ću izraz svakako pokrasti  , ali i dalje baš ne vidim jesam li dobro shvatio zadatak. Naime, , ali i dalje baš ne vidim jesam li dobro shvatio zadatak. Naime,  je svakako u intervalu koji si napisao, ali je svakako u intervalu koji si napisao, ali 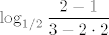 nije uopće definiran. Naime, nije uopće definiran. Naime, 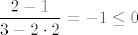 . .
Naprotiv, domena je 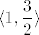 - relativno se lako vidi da je tada i samo tada - relativno se lako vidi da je tada i samo tada 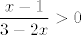 , što nam je potrebno. Mislim da je skup rješenja , što nam je potrebno. Mislim da je skup rješenja 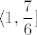 , ali to baš i nisam pretjerano provjeravao - u svakom slučaju, račun sam po sebi ne bi trebao biti težak - zanima te kad je , ali to baš i nisam pretjerano provjeravao - u svakom slučaju, račun sam po sebi ne bi trebao biti težak - zanima te kad je 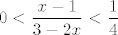 . . 
Sad ne znam, možda sam ja nešto zaznuo, možda tu fale neke zagrade, štoli, ali, sve u svemu, trenutno ni ja to ne mogu objasniti. 
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 12:43 pon, 1. 3. 2010 Naslov: Postano: 12:43 pon, 1. 3. 2010 Naslov: |
    |
|
|
Idemo iz početka...
[latex]\log_\frac{1}{2} \frac{x-1}{3-2x} - 2 \geq 0 \\
\log_{2^{-1}} \frac{x-1}{3-2x} \geq 2 \\
- \log_2 \frac{x-1}{3-2x} \geq \log_2 4 \\
\log_2 \left(\frac{x-1}{3-2x}\right)^{-1} \geq \log_2 4 \\
antilogaritmirajmo! \\
\frac{3-2x}{x-1} \geq 4 \\
\frac{3-2x}{x-1}-4 \geq 0 \\
\frac{3-2x-4x+4}{x-1} \geq 0 \\
\frac{-6x+7}{x-1} \geq 0[/latex]
Dakle, u ovom zadatku ima dva uvjeta:
1. uvjet je [latex]\frac{-6x+7}{x-1} \geq 0[/latex]
2. uvjet je da je argument logaritma strogo veći od nula, odnosno [latex]\frac{x-1}{3-2x} > 0[/latex]
Ovakve stvarčice već znaš rješavati. Na kraju napraviš presjek prvog i drugog rješenja.
Upozorenje...nisam si ovo raspisivao na papir, već sam tipkao i rješavao u glavi. Moguće da postoji koja greška, pa molim te pitaj ako ti nije jasno odakle sam nešto dobio ili ukoliko primjetiš neku grešku.
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
Hm.....sad kad sam pogledao mornikovo rješenje išao sam svoje rješiti do kraja na papiru... dobijem konačno rješenje [latex]x \in \left<1, \frac{3}{2}\right>[/latex].
Da nije možda zadatak glasio [latex]\log_\frac{1}{2} \left(\frac{x-1}{3-2x} - 2\right) \geq 0[/latex]?
E da, ja sam rješavao zadatak tako da sam bazu logaritma prebacio u onu veću od 1... Valjda ti je jasno što sam sve radio. Nije to nužno, ali meni nekako draže. :D
Idemo iz početka...
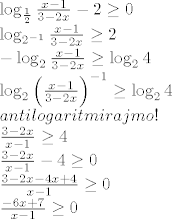
Dakle, u ovom zadatku ima dva uvjeta:
1. uvjet je 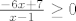
2. uvjet je da je argument logaritma strogo veći od nula, odnosno 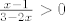
Ovakve stvarčice već znaš rješavati. Na kraju napraviš presjek prvog i drugog rješenja.
Upozorenje...nisam si ovo raspisivao na papir, već sam tipkao i rješavao u glavi. Moguće da postoji koja greška, pa molim te pitaj ako ti nije jasno odakle sam nešto dobio ili ukoliko primjetiš neku grešku.
Added after 4 minutes:
Hm.....sad kad sam pogledao mornikovo rješenje išao sam svoje rješiti do kraja na papiru... dobijem konačno rješenje 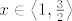 . .
Da nije možda zadatak glasio 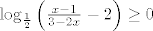 ? ?
E da, ja sam rješavao zadatak tako da sam bazu logaritma prebacio u onu veću od 1... Valjda ti je jasno što sam sve radio. Nije to nužno, ali meni nekako draže. 
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:52 pon, 1. 3. 2010 Naslov: Postano: 12:52 pon, 1. 3. 2010 Naslov: |
    |
|
|
Kenny, jesi li siguran da ti je [latex]\displaystyle\langle 1,\frac{3}{2}\rangle[/latex] konačno rješenje? Mislim da je to domena, a da je konačno rješenje ono što sam ja gore napisao (dakle, domena presječena ovim drugim uvjetom). Uzmi, na primjer, [latex]x=1.4[/latex] - to je u domeni, a nije u skupu rješenja. :)
A što se tiče mogućnosti da je [latex]-2[/latex] isto u argumentu logaritma - ni to ne daje ni rješenje ni domenu kakvu je ivicasb1 spomenuo - domena bi bila [latex]\displaystyle\langle\frac{7}{5},\frac{3}{2}\rangle[/latex], ako se ne varam. :)
Kenny, jesi li siguran da ti je 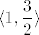 konačno rješenje? Mislim da je to domena, a da je konačno rješenje ono što sam ja gore napisao (dakle, domena presječena ovim drugim uvjetom). Uzmi, na primjer, konačno rješenje? Mislim da je to domena, a da je konačno rješenje ono što sam ja gore napisao (dakle, domena presječena ovim drugim uvjetom). Uzmi, na primjer,  - to je u domeni, a nije u skupu rješenja. - to je u domeni, a nije u skupu rješenja. 
A što se tiče mogućnosti da je 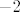 isto u argumentu logaritma - ni to ne daje ni rješenje ni domenu kakvu je ivicasb1 spomenuo - domena bi bila isto u argumentu logaritma - ni to ne daje ni rješenje ni domenu kakvu je ivicasb1 spomenuo - domena bi bila 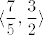 , ako se ne varam. , ako se ne varam. 
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:52 uto, 2. 3. 2010 Naslov: Postano: 20:52 uto, 2. 3. 2010 Naslov: |
    |
|
|
[quote="ivicasb1"]Evo ako moze malo od osnova ( nekad me pri rjesavanju naprave nesigurnim :shock: ) da mi netko objasni :
Situacija kad imamo recimo
[latex]2x -1 \geq 0[/latex]
[latex] 2x\geq 1~ /:2 [/latex]
[latex]x \leq \frac {1}{2}[/latex]
da li se ovdje mjenja predznak kada se dijeli i ako se jos negdje mijenja gdje( pri kojim situacijama ) ---znam ljudi , znam ....smijesno ,ali eto istinito!
2.stvar kod kompozicija funkcija zadatak glasi ovako :
Zadane su funkcije f(x)= cos 2x i g(x) = [latex]\frac{1}{2} arccosx[/latex]
sve sam zadatke sa kompozicijama rijesio samoovaj ne znam, pa ako mi ga netko moze objasniti ,puno hvala![/quote]
Dosta korisno bi bilo malo artikuliranije pisati tako da se lakše razumije što želiš. :)
Što se tiče dijeljenja s ne-nul realnim brojevima, predznak se mijenja samo ako se dijeli negativnim brojem. Ako nisi siguran u svoj postupak, korisno je provjeriti da li se krajnji uvjet na x (tj. [latex]x\leq\frac{1}{2}[/latex] ) slaže s početnim ([latex]2x-1\geq 0[/latex]). Ako uzmeš npr x=0, jasno je [latex]0\leq\frac{1}{2}[/latex], ali nije [latex]2\cdot 0 - 1 \geq 0[/latex].
Što se tiče pod 2. - kako uopće glasi zadatak? Napisati kompoziciju (ako da, koju? [latex]f\circ g[/latex] ili [latex]g\circ f[/latex]?), naći domenu (ako da, opet, domenu koje kompozicije), napisati te funkcije kao kompoziciju elementarnih funkcija ili nešto četvrto?
| ivicasb1 (napisa): | Evo ako moze malo od osnova ( nekad me pri rjesavanju naprave nesigurnim  ) da mi netko objasni : ) da mi netko objasni :
Situacija kad imamo recimo
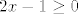
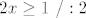
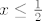
da li se ovdje mjenja predznak kada se dijeli i ako se jos negdje mijenja gdje( pri kojim situacijama ) —znam ljudi , znam ....smijesno ,ali eto istinito!
2.stvar kod kompozicija funkcija zadatak glasi ovako :
Zadane su funkcije f(x)= cos 2x i g(x) = 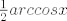
sve sam zadatke sa kompozicijama rijesio samoovaj ne znam, pa ako mi ga netko moze objasniti ,puno hvala! |
Dosta korisno bi bilo malo artikuliranije pisati tako da se lakše razumije što želiš. 
Što se tiče dijeljenja s ne-nul realnim brojevima, predznak se mijenja samo ako se dijeli negativnim brojem. Ako nisi siguran u svoj postupak, korisno je provjeriti da li se krajnji uvjet na x (tj. 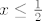 ) slaže s početnim ( ) slaže s početnim (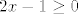 ). Ako uzmeš npr x=0, jasno je ). Ako uzmeš npr x=0, jasno je 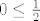 , ali nije , ali nije 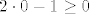 . .
Što se tiče pod 2. - kako uopće glasi zadatak? Napisati kompoziciju (ako da, koju? 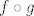 ili ili 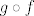 ?), naći domenu (ako da, opet, domenu koje kompozicije), napisati te funkcije kao kompoziciju elementarnih funkcija ili nešto četvrto? ?), naći domenu (ako da, opet, domenu koje kompozicije), napisati te funkcije kao kompoziciju elementarnih funkcija ili nešto četvrto?
_________________
The Dude Abides
Zadnja promjena: goranm; 22:38 uto, 2. 3. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:43 uto, 2. 3. 2010 Naslov: Postano: 22:43 uto, 2. 3. 2010 Naslov: |
    |
|
|
Kod kompozicije [latex]f\circ g[/latex], u f(x) moraš umjesto x uvrstiti g(x), tj.
[latex](f\circ g) (x)=f(g(x))=f(\frac{1}{2}\arccos{x})=cos{\left(2\cdot\frac{1}{2}\arccos{x}\right)}[/latex]
To se još može srediti, ali to tebi ostavljam. Druga kompozicija, [latex]g\circ f[/latex], se na isti način rješava.
Kod kompozicije 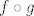 , u f(x) moraš umjesto x uvrstiti g(x), tj. , u f(x) moraš umjesto x uvrstiti g(x), tj.
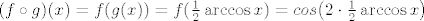
To se još može srediti, ali to tebi ostavljam. Druga kompozicija, 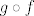 , se na isti način rješava. , se na isti način rješava.
_________________
The Dude Abides
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
|












