| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:58 čet, 4. 3. 2010 Naslov: Postano: 13:58 čet, 4. 3. 2010 Naslov: |
    |
|
|
[quote="ivicasb1"]e sad ne razumijem sljedeca dva koraka, kako su oni dobiveni ?( u ovim rjesenjima sto ja imam su preskakani neki koraci -a oni mi fale da bi skuzio )
[latex]22^x = \frac{13-15y}{5y-1}[/latex]
[latex](5y-1)22^x = 13 -15 y[/latex]
Bio bih zahvalan na konstruktivnim objasnjenjima, hvala.[/quote]
Prvi korak je definicija logaritma. Ako je [latex]x=b^y[/latex] onda je [latex]y=\log_b{x}[/latex]. To je nešto što ti sigurno piše u udžbeniku (ako se ne varam, za 2. srednje), a i nije teško sam istražiti. Npr. ako u google upišeš logaritam, odvest će te na http://hr.wikipedia.org/wiki/Logaritam
U drugom koraku je sve pomnoženo nazivnikom 5y-1.
| ivicasb1 (napisa): | e sad ne razumijem sljedeca dva koraka, kako su oni dobiveni ?( u ovim rjesenjima sto ja imam su preskakani neki koraci -a oni mi fale da bi skuzio )
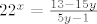
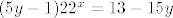
Bio bih zahvalan na konstruktivnim objasnjenjima, hvala. |
Prvi korak je definicija logaritma. Ako je 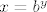 onda je onda je 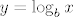 . To je nešto što ti sigurno piše u udžbeniku (ako se ne varam, za 2. srednje), a i nije teško sam istražiti. Npr. ako u google upišeš logaritam, odvest će te na http://hr.wikipedia.org/wiki/Logaritam . To je nešto što ti sigurno piše u udžbeniku (ako se ne varam, za 2. srednje), a i nije teško sam istražiti. Npr. ako u google upišeš logaritam, odvest će te na http://hr.wikipedia.org/wiki/Logaritam
U drugom koraku je sve pomnoženo nazivnikom 5y-1.
_________________
The Dude Abides
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 20:38 čet, 4. 3. 2010 Naslov: Postano: 20:38 čet, 4. 3. 2010 Naslov: |
    |
|
|
hvala gorane, ljepo objasnjeno , skuzio sam :) Meni je malo problem jer mi fali malo predznanja iz srednje i to me je sad sustiglo na faksu :shock:
Neke osnove iz logaritama, sin,cos- ta pravila,sta je cemu jednako, sta proizlazi iz cega,malo sam trazio po netu i nesto malo naso,
Jel ima taj udzbenik sto si spomenio negdje na netu u digitalnom obliku ili neka skripta dobra gdje to ima sazeto da to malo predem?
Hvala
hvala gorane, ljepo objasnjeno , skuzio sam  Meni je malo problem jer mi fali malo predznanja iz srednje i to me je sad sustiglo na faksu Meni je malo problem jer mi fali malo predznanja iz srednje i to me je sad sustiglo na faksu 
Neke osnove iz logaritama, sin,cos- ta pravila,sta je cemu jednako, sta proizlazi iz cega,malo sam trazio po netu i nesto malo naso,
Jel ima taj udzbenik sto si spomenio negdje na netu u digitalnom obliku ili neka skripta dobra gdje to ima sazeto da to malo predem?
Hvala
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
derle
Forumaš(ica)


Pridružen/a: 28. 05. 2005. (17:53:46)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
derle
Forumaš(ica)


Pridružen/a: 28. 05. 2005. (17:53:46)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 21:12 ned, 14. 3. 2010 Naslov: Postano: 21:12 ned, 14. 3. 2010 Naslov: |
    |
|
|
Arkus kosinus je definiran na segmentu [latex][-1, 1][/latex], pa je ono što ti ovdje moraš napraviti jest rješiti ovo:
[latex]-1 \le \frac{x^2+x}{x^2-5x+4} \le 1[/latex] (pretpostavljam da si napravio grešku u pisanju brojnika - molim provjeri!).
Odnosno, moraš rješiti:[latex] -1 \le \frac{x^2+x}{x^2-5x+4}[/latex] i [latex]\frac{x^2+x}{x^2-5x+4} \le 1[/latex].
[latex]
-1 \le \frac{x^2+x}{x^2-5x+4} \\
\frac{x^2+x}{x^2-5x+4} \geq -1 \\
\frac{x^2+x}{x^2-5x+4} +1 \geq 0 \\
\frac{x^2+x+x^2-5x+4}{x^2-5x+4} \geq 0 \\
\frac{2x^2-4x+4}{x^2-5x+4} \geq 0[/latex]
Ovo smo ti već prije objašnjavali kako se rješava, pa ću samo napisati da je rješenje ovog slučaja [latex]x \in <-\infty, 1> \cup <4, +\infty>[/latex].
Analogno rješavamo i drugi dio, pa dobijemo [latex]x \in <-\infty, \frac{2}{3}] \cup <1, 4>[/latex].
Rješenje je presjek tih dvaju rješenja, odnosno [latex]x \in <-\infty, \frac{2}{3}][/latex]
Arkus kosinus je definiran na segmentu 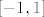 , pa je ono što ti ovdje moraš napraviti jest rješiti ovo: , pa je ono što ti ovdje moraš napraviti jest rješiti ovo:
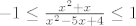 (pretpostavljam da si napravio grešku u pisanju brojnika - molim provjeri!). (pretpostavljam da si napravio grešku u pisanju brojnika - molim provjeri!).
Odnosno, moraš rješiti: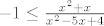 i i 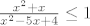 . .
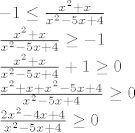
Ovo smo ti već prije objašnjavali kako se rješava, pa ću samo napisati da je rješenje ovog slučaja 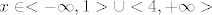 . .
Analogno rješavamo i drugi dio, pa dobijemo 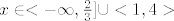 . .
Rješenje je presjek tih dvaju rješenja, odnosno 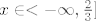
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 13:00 pon, 15. 3. 2010 Naslov: Postano: 13:00 pon, 15. 3. 2010 Naslov: |
    |
|
|
E kenny hvala puno na rjesenju, imas pravo potkrala se pogreskica koju si ti odmah uocio u brojniku nije[latex]x^2 nego- samo- [/latex] x
I tvoje se rjesenje podudara sa rjesenjem koje ja imam! Bravo 8)
[size=9][color=#999999]Added after 18 minutes:[/color][/size]
hej kenny ajd molim te ,ako ti nije problem rijesiti mi
[latex]\frac{2x^2-4x+4}{x^2-5x+4} \geq 0[/latex]
odavde pa do rjesenja, ja sam pokusao pa sam se spetljo skroz, mama mia :shock:
ili mi reci samo ukratko kako da rjesim,thx
[size=9][color=#999999]Added after 56 minutes:[/color][/size]
E ipak sam ga uspio rjesiti :D
Imam jos jedan analogan zadatak pa cu se baciti na morenje spomenutog :lol:
Imam jedno podpitanjce:
Kada imamo situaciju kao gore u zadatku, da se u brojniku nalaze i pozitivni i negativni brojevi,nepoznanice, kako se onda njih tretira u odnosu na znak > ili <, znam kakva je procedura kada su brojnik i nazivnik pozitivni ili negativni i kada su razlicitog predznaka, ali kako se tretiraju kada imam vise znakova +, - ?
Ako itko skuzi sta sam pitao nek mi molim i objasni :o
Hvala
E kenny hvala puno na rjesenju, imas pravo potkrala se pogreskica koju si ti odmah uocio u brojniku nije x x
I tvoje se rjesenje podudara sa rjesenjem koje ja imam! Bravo 
Added after 18 minutes:
hej kenny ajd molim te ,ako ti nije problem rijesiti mi
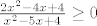
odavde pa do rjesenja, ja sam pokusao pa sam se spetljo skroz, mama mia 
ili mi reci samo ukratko kako da rjesim,thx
Added after 56 minutes:
E ipak sam ga uspio rjesiti 
Imam jos jedan analogan zadatak pa cu se baciti na morenje spomenutog 
Imam jedno podpitanjce:
Kada imamo situaciju kao gore u zadatku, da se u brojniku nalaze i pozitivni i negativni brojevi,nepoznanice, kako se onda njih tretira u odnosu na znak > ili <, znam kakva je procedura kada su brojnik i nazivnik pozitivni ili negativni i kada su razlicitog predznaka, ali kako se tretiraju kada imam vise znakova +, - ?
Ako itko skuzi sta sam pitao nek mi molim i objasni 
Hvala
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 16:05 pet, 9. 4. 2010 Naslov: Postano: 16:05 pet, 9. 4. 2010 Naslov: |
    |
|
|
Znam da je malo kasni odgovor :) (koga lažem, kriminalno kasnim :D), ali ajde, budući da je još neodgovoreno... :)
Dakle, ne znam baš kako pomoći pri crtanju grafa, vjerojatno je najjednostavnije uzeti par točaka (potencije od [latex]2[/latex] come to mind :)) i nacrtati neku krivulju između njih :D, ali probajmo ovako. Pretpostavljam da [latex]\log x[/latex] (dakle, logaritam s bazom [latex]10[/latex]) znaš nacrtati - ako ne, tu ti nažalost ne mogu pomoći nikako osim da opet kažem da uzmeš par točaka pa tako nacrtaš krivulju...
Sad, primijeti da je [latex]\displaystyle \log_{1/2}{x}=\frac{\log{x}}{\log{1/2}}[/latex] - to slijedi iz tvrdnje koju ste sigurno spominjali: [latex]\displaystyle \log_a{b}=\frac{\log_c{b}}{\log_c{a}}[/latex], a i koju nije pretjerano teško za dokazati (reci ako ne uspiješ sam). Kako je [latex]\log 1/2[/latex] negdje oko [latex]-0.3[/latex], zapravo imaš da je [latex]\log_{1/2}{x}[/latex] otprilike [latex]-\displaystyle\frac{10}{3}\log{x}[/latex], a to onda znaš nacrtati - samo "izokreneš" graf od logaritma i onda još svaku vrijednost pomnožiš s [latex]\frac{10}{3}[/latex], što bi reklo da graf "proširiš" malo više od tri puta, ne znam baš kako to bolje objasniti. :)
Znam da je malo kasni odgovor  (koga lažem, kriminalno kasnim (koga lažem, kriminalno kasnim  ), ali ajde, budući da je još neodgovoreno... ), ali ajde, budući da je još neodgovoreno... 
Dakle, ne znam baš kako pomoći pri crtanju grafa, vjerojatno je najjednostavnije uzeti par točaka (potencije od  come to mind come to mind  ) i nacrtati neku krivulju između njih ) i nacrtati neku krivulju između njih  , ali probajmo ovako. Pretpostavljam da , ali probajmo ovako. Pretpostavljam da 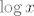 (dakle, logaritam s bazom (dakle, logaritam s bazom  ) znaš nacrtati - ako ne, tu ti nažalost ne mogu pomoći nikako osim da opet kažem da uzmeš par točaka pa tako nacrtaš krivulju... ) znaš nacrtati - ako ne, tu ti nažalost ne mogu pomoći nikako osim da opet kažem da uzmeš par točaka pa tako nacrtaš krivulju...
Sad, primijeti da je 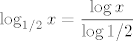 - to slijedi iz tvrdnje koju ste sigurno spominjali: - to slijedi iz tvrdnje koju ste sigurno spominjali: 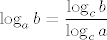 , a i koju nije pretjerano teško za dokazati (reci ako ne uspiješ sam). Kako je , a i koju nije pretjerano teško za dokazati (reci ako ne uspiješ sam). Kako je 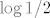 negdje oko negdje oko 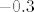 , zapravo imaš da je , zapravo imaš da je 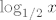 otprilike otprilike 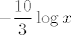 , a to onda znaš nacrtati - samo "izokreneš" graf od logaritma i onda još svaku vrijednost pomnožiš s , a to onda znaš nacrtati - samo "izokreneš" graf od logaritma i onda još svaku vrijednost pomnožiš s 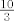 , što bi reklo da graf "proširiš" malo više od tri puta, ne znam baš kako to bolje objasniti. , što bi reklo da graf "proširiš" malo više od tri puta, ne znam baš kako to bolje objasniti. 
|
|
| [Vrh] |
|
anđi
Forumaš(ica)

Pridružen/a: 23. 10. 2010. (12:34:52)
Postovi: (1)16
|
 Postano: 14:48 sub, 23. 10. 2010 Naslov: Re: Funkcije Postano: 14:48 sub, 23. 10. 2010 Naslov: Re: Funkcije |
    |
|
|
[quote="astrmastr"]zbog nekih mutnih :wink: razloga nisam mogao prisustvovat na odredenim vjezbama, te imam problema sa odredjenim zadatcima :oops: , te bih cijenio da netko samo objasni kako se generalno rijesavaju ovakvi zadatci :weee:
1.
Postoji li padajuca funkcija f : R -> R takva da je funkcija g : R -> R defnirana formulom
[latex]g:= 4^f-2^f[/latex]
strogo rastuca? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u protivnom
dokazite da takva funkcija f ne postoji.
2.
Postoji li injekcija f : R -> R takva da je funkcija g : R -> R definirana formulom
[latex]g(x) := f(4^x-2^x)[/latex]
surjekcija? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u protivnom
dokazite da takva funkcija f ne postoji.
3.
Postoji li surjekcija f : R ->R takva da je funkcija g : R -> R definirana formulom
[latex]g(x) := f(9^x + 3^x)[/latex]
bijekcija? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u protivnom
dokazite da takva funkcija f ne postoji.
4.
Postoji li surjekcija f : R -> R takva da je funkcija g : R -> R definirana formulom
[latex]g(x) := f(x)^5 + f(x)^2[/latex]
strogo padajuca? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u pro-
tivnom dokazite da takva funkcija f ne postoji.
5.
(a) Dokazite da je
[latex]f(x) = 4^x-2^{(x+1)}+|2^x-1|-1[/latex]
injekcija na <-inf,0] i odredite joj inverz na <-inf,0]
(b) Neka su f:R -> R i g:R -> R funkcije takve da je
g(f(x)) = sh x; za svaki xeR
Je li f injekcija?
:grebgreb:[/quote] :)
| astrmastr (napisa): | zbog nekih mutnih  razloga nisam mogao prisustvovat na odredenim vjezbama, te imam problema sa odredjenim zadatcima razloga nisam mogao prisustvovat na odredenim vjezbama, te imam problema sa odredjenim zadatcima  , te bih cijenio da netko samo objasni kako se generalno rijesavaju ovakvi zadatci , te bih cijenio da netko samo objasni kako se generalno rijesavaju ovakvi zadatci 
1.
Postoji li padajuca funkcija f : R → R takva da je funkcija g : R → R defnirana formulom
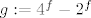
strogo rastuca? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u protivnom
dokazite da takva funkcija f ne postoji.
2.
Postoji li injekcija f : R → R takva da je funkcija g : R → R definirana formulom
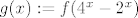
surjekcija? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u protivnom
dokazite da takva funkcija f ne postoji.
3.
Postoji li surjekcija f : R →R takva da je funkcija g : R → R definirana formulom
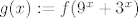
bijekcija? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u protivnom
dokazite da takva funkcija f ne postoji.
4.
Postoji li surjekcija f : R → R takva da je funkcija g : R → R definirana formulom
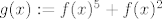
strogo padajuca? U slucaju potvrdnog odgovora nadite primjer takve funkcije f, a u pro-
tivnom dokazite da takva funkcija f ne postoji.
5.
(a) Dokazite da je
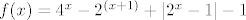
injekcija na ←inf,0] i odredite joj inverz na ←inf,0]
(b) Neka su f:R → R i g:R → R funkcije takve da je
g(f(x)) = sh x; za svaki xeR
Je li f injekcija?
 |

|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
dodoria
Forumaš(ica)

Pridružen/a: 04. 10. 2011. (13:31:15)
Postovi: (E)16
|
|
| [Vrh] |
|
|










