| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gego
Forumaš(ica)

Pridružen/a: 20. 09. 2009. (21:10:55)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
gego
Forumaš(ica)

Pridružen/a: 20. 09. 2009. (21:10:55)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:34 ned, 4. 4. 2010 Naslov: Postano: 11:34 ned, 4. 4. 2010 Naslov: |
    |
|
|
Ovako, pokušat ću ja odgovorit da vidim jesam li pohvatao postupak i to :D
Znači, elemente baze označiš sa [latex]e_{1}=1-t-t^{2},\ \ e_{2}=1+t,\ \ e_{3}=t-t^{2},\ \ e_{4}=t+t^{3}.[/latex]
Sada, kao što je pmli rekao. gledaš djelovanje funkcionala na elemente baze. Vidimo da je općenito djelovanje funkcionala zadano sa [latex]f^{*}(p)=p(-1)+p(1)+p(0).[/latex]
Znači, sada imamo:
[latex]f^{*}(e_{1})=(1-t-t^{2})(-1)+(1-t-t^{2})(1)+(1-t-t^{2})(1)(0)=1-1+1=1=\alpha_1
\\ f^{*}(e_{2})=0+2+1=3=\alpha_2
\\ f^{*}(e_{3})=-2+0+0=-2=\alpha_3
\\ f^{*}(e_{4})=-2+2+0=0=\alpha_4
[/latex]
Sada je prikaz [latex]f^{*}[/latex] u dualnoj bazi:
[latex]f^{*}=f_{1}^{*}+3f_{2}^{*}-2f_{3}^{*}[/latex]
Ovako, pokušat ću ja odgovorit da vidim jesam li pohvatao postupak i to 
Znači, elemente baze označiš sa 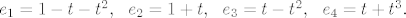
Sada, kao što je pmli rekao. gledaš djelovanje funkcionala na elemente baze. Vidimo da je općenito djelovanje funkcionala zadano sa 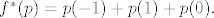
Znači, sada imamo:
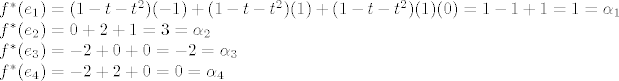
Sada je prikaz 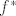 u dualnoj bazi: u dualnoj bazi:
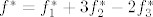
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:25 ned, 4. 4. 2010 Naslov: Postano: 12:25 ned, 4. 4. 2010 Naslov: |
    |
|
|
Pitanje vezano uz anihilatore, iz 2004., 2. zadatak http://web.math.hr/nastava/la/kolokviji/02-03/la2/kol1a.pdf
Dobio sam bazu za anihilator:
[latex]L^{0}=\{d,a+b+c \}[/latex]
i sad me traži nadopunu za dualni prostor. Da li je dobra nadopuna {b,c} ili se drugačije radi kod dualnog prostora?
I 5. zadatak iz 2006. http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf
Znam da je uvjet da se matrica može dijagonalizirati da sve svojstvene vrijednosti imaju jednake algebarske i geometrijske kratnosti, ali ne znam kako točno ovo dokazati.
Pitanje vezano uz anihilatore, iz 2004., 2. zadatak http://web.math.hr/nastava/la/kolokviji/02-03/la2/kol1a.pdf
Dobio sam bazu za anihilator:
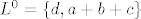
i sad me traži nadopunu za dualni prostor. Da li je dobra nadopuna {b,c} ili se drugačije radi kod dualnog prostora?
I 5. zadatak iz 2006. http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1a.pdf
Znam da je uvjet da se matrica može dijagonalizirati da sve svojstvene vrijednosti imaju jednake algebarske i geometrijske kratnosti, ali ne znam kako točno ovo dokazati.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:46 ned, 4. 4. 2010 Naslov: Postano: 12:46 ned, 4. 4. 2010 Naslov: |
    |
|
|
Za ovo prvo, mislim da link nije dobar. Kako god, bilo bi preciznije pisati [latex]L^0 = \{e_1^*, e_2^*\}[/latex]. Što se tiče nadopune dualne baze, to ne trebaš raditi ako ideš postupkom koji smo radili na vježbama. Nađeš bazu za [latex]L[/latex] ([latex]k[/latex] njih), nadopuniš je do baze za [latex]V[/latex] ([latex]n[/latex] komada), odrediš njenu dualnu bazu, pa ti onih [latex]n-k[/latex] zadnjih fukcionala čini bazu za [latex]L^0[/latex]. Pimjeti da si u ovom postupku već odredio bazu za [latex]V^*[/latex].
Vezano uz 5. zadatak, uzmi neki svojstveni vektor [latex]x_i[/latex] pridružen svojstvenoj vrijednosti [latex]\lambda_i[/latex], pa se malo igraj s izrazom [latex](AB)x_i = (BA)x_i[/latex]. :D
Za ovo prvo, mislim da link nije dobar. Kako god, bilo bi preciznije pisati 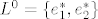 . Što se tiče nadopune dualne baze, to ne trebaš raditi ako ideš postupkom koji smo radili na vježbama. Nađeš bazu za . Što se tiče nadopune dualne baze, to ne trebaš raditi ako ideš postupkom koji smo radili na vježbama. Nađeš bazu za  ( ( njih), nadopuniš je do baze za njih), nadopuniš je do baze za 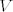 ( ( komada), odrediš njenu dualnu bazu, pa ti onih komada), odrediš njenu dualnu bazu, pa ti onih 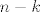 zadnjih fukcionala čini bazu za zadnjih fukcionala čini bazu za 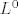 . Pimjeti da si u ovom postupku već odredio bazu za . Pimjeti da si u ovom postupku već odredio bazu za 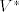 . .
Vezano uz 5. zadatak, uzmi neki svojstveni vektor 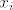 pridružen svojstvenoj vrijednosti pridružen svojstvenoj vrijednosti 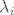 , pa se malo igraj s izrazom , pa se malo igraj s izrazom 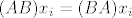 . . 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:24 ned, 4. 4. 2010 Naslov: Postano: 13:24 ned, 4. 4. 2010 Naslov: |
    |
|
|
Točno, malo sam se neprecizno izrazio, ja sam u bazi za anihilator napisao odmah djelovanje na proizvoljan p. A što se tiče nadopune, da, dobio sam ju tim postupkom ali sam mehanički razmišljao pa nisam ni primijetio to.
I što se tiče prvog zadatka u http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1_p.pdf ja sam dobio sljedeće:
a) [latex]A(b,b) = I(b,a) \cdot A(a,a) \cdot I(a,b)[/latex], gdje je [latex]A(a,a)[/latex] ova zadana matrica u zadatku.
b) [latex]A(b,a)=I(b,a) \cdot A(a,a)[/latex]
Može li se ovaj [latex]I(a,b)[/latex] naći na neki brži način nego preko traženja koeficijenata za svaki I(b) u bazi a?
Točno, malo sam se neprecizno izrazio, ja sam u bazi za anihilator napisao odmah djelovanje na proizvoljan p. A što se tiče nadopune, da, dobio sam ju tim postupkom ali sam mehanički razmišljao pa nisam ni primijetio to.
I što se tiče prvog zadatka u http://web.math.hr/nastava/la/kolokviji/05-06/la2/kol1_p.pdf ja sam dobio sljedeće:
a) 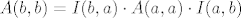 , gdje je , gdje je 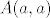 ova zadana matrica u zadatku. ova zadana matrica u zadatku.
b) 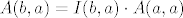
Može li se ovaj 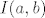 naći na neki brži način nego preko traženja koeficijenata za svaki I(b) u bazi a? naći na neki brži način nego preko traženja koeficijenata za svaki I(b) u bazi a?
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
 Postano: 13:31 ned, 4. 4. 2010 Naslov: Postano: 13:31 ned, 4. 4. 2010 Naslov: |
    |
|
|
mozes... I(b,a) mozes dobiti tako da uvedes kanonsku bazu za R3 i oznacis je recimo sa g i onda imas I(b,a)=I(b,g)*I(g,a) a I(b,g) ti je zapravo I(g,b)^-1
mozes... I(b,a) mozes dobiti tako da uvedes kanonsku bazu za R3 i oznacis je recimo sa g i onda imas I(b,a)=I(b,g)*I(g,a) a I(b,g) ti je zapravo I(g,b)^-1
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|














