|
Uspio sam ovo rjesiti, no sada imam jos zanimljivije pitanje. Neka su [latex]t_1,\dots,t_l[/latex], točke koje su vrhovi simpleksa dobivenog u prethodnom koraku, te neka su [latex]d_1,\dots,d_l[/latex] udaljenosti točke [latex]y[/latex] od (redom) točaka [latex]t_1,\dots,t_l[/latex]. Nadimo relativne udaljenosti, odnosno neka [latex]d'_i=\frac{d_i}{\sum_{k=1}^ld_k}[/latex]. Sada deformiramo naš simpleks na određeni način, i dobijemo [latex]\Delta'[/latex], tako da su sada [latex]t'_1,\dots,t'_l[/latex] vrhovi novog simpleksa.
Kako naći točku [latex]y'[/latex] (ponovno u interijeru, ali sada od [latex]\Delta'[/latex]), takvu da je relativna udaljenost te točke od svakog od novih vrhova [latex]t'_j[/latex], jednaka baš [latex]d'_j[/latex]? Dakle, poanta je da nakon deformacije simpleksa nađemo točku u novom simpleksu koja odgovara staroj točki (u starom simpleksu).
Ponovno, svaka sugestija je dobro dosla, te bi volio da se netko od profesora/asistenata ukljuci u raspravu. Ovaj mi se problem (zasada) čini težim od prethodnog.
Uspio sam ovo rjesiti, no sada imam jos zanimljivije pitanje. Neka su 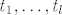 , točke koje su vrhovi simpleksa dobivenog u prethodnom koraku, te neka su , točke koje su vrhovi simpleksa dobivenog u prethodnom koraku, te neka su  udaljenosti točke udaljenosti točke  od (redom) točaka od (redom) točaka 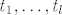 . Nadimo relativne udaljenosti, odnosno neka . Nadimo relativne udaljenosti, odnosno neka 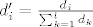 . Sada deformiramo naš simpleks na određeni način, i dobijemo . Sada deformiramo naš simpleks na određeni način, i dobijemo  , tako da su sada , tako da su sada  vrhovi novog simpleksa. vrhovi novog simpleksa.
Kako naći točku 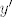 (ponovno u interijeru, ali sada od (ponovno u interijeru, ali sada od  ), takvu da je relativna udaljenost te točke od svakog od novih vrhova ), takvu da je relativna udaljenost te točke od svakog od novih vrhova 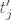 , jednaka baš , jednaka baš 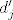 ? Dakle, poanta je da nakon deformacije simpleksa nađemo točku u novom simpleksu koja odgovara staroj točki (u starom simpleksu). ? Dakle, poanta je da nakon deformacije simpleksa nađemo točku u novom simpleksu koja odgovara staroj točki (u starom simpleksu).
Ponovno, svaka sugestija je dobro dosla, te bi volio da se netko od profesora/asistenata ukljuci u raspravu. Ovaj mi se problem (zasada) čini težim od prethodnog.
|




