| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 18:55 čet, 6. 5. 2010 Naslov: Postano: 18:55 čet, 6. 5. 2010 Naslov: |
    |
|
|
Lol, opce nisam skuzio kvadrat, sori...
ugl, prvi dio je isti, nazivnik namjestas na kvadrat... Ubrzo dobijes da je ovaj integral jednak integralu
[latex]\frac{16}{9}\int\frac{dx}{((\frac{2x+1}{\sqrt{3}})^2+1)^2}[/latex]
Sad bi mogli supstituciju stavit, npr [latex]t=\frac{2x+1}{\sqrt{3}}[/latex]
u tom slucaju integral bi se sveo na [latex]\int\frac{dt}{(t^2+1)^2}[/latex]
Ovaj je malo zeznut, al moze se rijesit uz malo podesavanje: dodamo i oduzmemo t^2 u brojniku pa imamo
[latex]\int \frac{1+t^2-t^2}{(t^2+1)^2}dt=\int\frac{dt}{t^2+1}-\int\frac{t^2}{(t^2+1)^2}[/latex] (to dobijemo kad razdvojimo)
Sad je ostalo tehnicko, prvi znamo - to je arctg(t), a drugi se moze parcijalno integrirati t.d. stavimo [latex]u=t, v'=\frac{t}{t^2+1}[/latex]
(gdje bi v' integrirali supstitucijom y=t^2)
Lol, opce nisam skuzio kvadrat, sori...
ugl, prvi dio je isti, nazivnik namjestas na kvadrat... Ubrzo dobijes da je ovaj integral jednak integralu
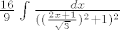
Sad bi mogli supstituciju stavit, npr 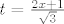
u tom slucaju integral bi se sveo na 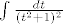
Ovaj je malo zeznut, al moze se rijesit uz malo podesavanje: dodamo i oduzmemo t^2 u brojniku pa imamo
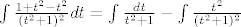 (to dobijemo kad razdvojimo) (to dobijemo kad razdvojimo)
Sad je ostalo tehnicko, prvi znamo - to je arctg(t), a drugi se moze parcijalno integrirati t.d. stavimo 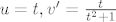
(gdje bi v' integrirali supstitucijom y=t^2)
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 12:43 sub, 8. 5. 2010 Naslov: Postano: 12:43 sub, 8. 5. 2010 Naslov: |
    |
|
|
[quote="lanek"]2. (c) iz zadaće?molim pomoć! :roll:[/quote]
možda cosx=t, x=arccost, na [0,pi] je cos bijekcija, pa to štima.
dobje se arccost/(1+t^2), pa to parcijalnom integracijom sa arccost=u, dv=ovo ostalo. Tak bi mislim trebalo proć, ali moguće da može i jednostavnije.
| lanek (napisa): | 2. (c) iz zadaće?molim pomoć!  |
možda cosx=t, x=arccost, na [0,pi] je cos bijekcija, pa to štima.
dobje se arccost/(1+t^2), pa to parcijalnom integracijom sa arccost=u, dv=ovo ostalo. Tak bi mislim trebalo proć, ali moguće da može i jednostavnije.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 12:40 ned, 9. 5. 2010 Naslov: Postano: 12:40 ned, 9. 5. 2010 Naslov: |
    |
|
|
Evo na jednom manjem intervalu:
[latex]\int_{0}^{2\pi} |sinx|dx [/latex]
sinus je pozitivan na [0,pi], i negativan na [pi,2pi]. Zato taj integral moramo razbiti na sumu integrala, ovako:
[latex]\int_{0}^{2\pi} |sinx|dx = \int_{0}^{\pi} |sinx|dx + \int_{\pi}^{2\pi} |sinx|dx[/latex]
na ovim intervalima znamo predznak od sinusa, pa dalje imamo
[latex] = \int_{0}^{\pi} sinxdx + \int_{\pi}^{2\pi} -sinxdx[/latex]
I sad dalje znaš.
Btw kada se računa površina ispod krivulje neke, onda isto moramo razbijat na interale po predznaku, da se ne bi "pozitivna površina" pokratila sa "negativnom"
Evo na jednom manjem intervalu:
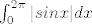
sinus je pozitivan na [0,pi], i negativan na [pi,2pi]. Zato taj integral moramo razbiti na sumu integrala, ovako:
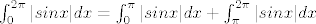
na ovim intervalima znamo predznak od sinusa, pa dalje imamo
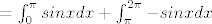
I sad dalje znaš.
Btw kada se računa površina ispod krivulje neke, onda isto moramo razbijat na interale po predznaku, da se ne bi "pozitivna površina" pokratila sa "negativnom"
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|





















