| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
 Postano: 12:03 uto, 11. 5. 2010 Naslov: linearna zavisnost i nezavisnost vektora Postano: 12:03 uto, 11. 5. 2010 Naslov: linearna zavisnost i nezavisnost vektora |
    |
|
|
Moze pomoc oko jednog zadatka? U ovisnosti o realnom parametru m ispitajte linearnu zavisnost i nezavisnost vektora (1,0,1),(m,m,0) i (m-1,1,-1).
Primjetio sam da smo na vjezbama radili slican zadatak prek determinante matrice, no nije mi to jasno. Moze li netko rijesiti detaljno zadatak s objasnjenjem... :D
hvala puno.
Moze pomoc oko jednog zadatka? U ovisnosti o realnom parametru m ispitajte linearnu zavisnost i nezavisnost vektora (1,0,1),(m,m,0) i (m-1,1,-1).
Primjetio sam da smo na vjezbama radili slican zadatak prek determinante matrice, no nije mi to jasno. Moze li netko rijesiti detaljno zadatak s objasnjenjem... 
hvala puno.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 13:04 uto, 11. 5. 2010 Naslov: Postano: 13:04 uto, 11. 5. 2010 Naslov: |
    |
|
|
Fora je da, ako imaš tri vektora, oni su zavisni akko im je mješoviti produkt jednak 0. Pokaže se da je, kada imaš vektore prikazane u kanonskoj bazi, mješoviti produkt jednak determinanti "matrice koeficijenata", kratko rečeno. Dakle, trebaš odrediti za koje m vrijedi [latex]\left|
\begin{array}{ccc}
1 & 0 & 1 \\
m & m & 0 \\
m-1 & 1 & -1
\end{array} \right| = 0[/latex] (za te m su vektori zavisni).
Fora je da, ako imaš tri vektora, oni su zavisni akko im je mješoviti produkt jednak 0. Pokaže se da je, kada imaš vektore prikazane u kanonskoj bazi, mješoviti produkt jednak determinanti "matrice koeficijenata", kratko rečeno. Dakle, trebaš odrediti za koje m vrijedi 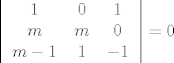 (za te m su vektori zavisni). (za te m su vektori zavisni).
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
|





