| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
 Postano: 12:32 uto, 11. 5. 2010 Naslov: algebra Postano: 12:32 uto, 11. 5. 2010 Naslov: algebra |
    |
|
|
ovo su zadaci sa vjezbi tako da su rijeseni, ali ipak mi nije sve jasno :D
Ako grupa G ima konacan broj podgrupa, tada je konačna.
pretpostavili smo da je G beskonacnog reda, i za svaki a iz G definirali G_a:= {a^n : n iz Z} <= G
sad je dovoljno pokazat da iz G_a=G_b slijedi da je a=b ili a=b^-1 jer onda imamo beskonacno mnogo podgrupa
G_a=G_b => a=b^n za neki n iz Z, uzmemo s min eksp vrijednoscu
b=a^m .... isto ko gore
pretp. |n|>=2 b=a^m=b^nm => nm = 1
evo, to mi nije jasno, zasto slijedi da je nm jednako 1? zasto b ne bi mogao biti element konacnog reda?
ovo su zadaci sa vjezbi tako da su rijeseni, ali ipak mi nije sve jasno 
Ako grupa G ima konacan broj podgrupa, tada je konačna.
pretpostavili smo da je G beskonacnog reda, i za svaki a iz G definirali G_a:= {a^n : n iz Z} <= G
sad je dovoljno pokazat da iz G_a=G_b slijedi da je a=b ili a=b^-1 jer onda imamo beskonacno mnogo podgrupa
G_a=G_b => a=b^n za neki n iz Z, uzmemo s min eksp vrijednoscu
b=a^m .... isto ko gore
pretp. |n|>=2 b=a^m=b^nm => nm = 1
evo, to mi nije jasno, zasto slijedi da je nm jednako 1? zasto b ne bi mogao biti element konacnog reda?
_________________
Nov, još gluplji.
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
 Postano: 17:55 uto, 11. 5. 2010 Naslov: Postano: 17:55 uto, 11. 5. 2010 Naslov: |
    |
|
|
Neka je G Abelova grupa. Definiramo T:={a iz G: |a|=p}. Tada je T<=G.
ja nemam svoje vjezbe da se razumijemo, i nisam bila nikad na vjezbama pa desifriram fotokopije.
u prvom redu pise komentar pretpostavljam studenta cije su to biljeske (cini se da je zadatak bio za zadacu) da za p razlicit od 1 unutra nije e pa to ne moze biti podgrupa, dobro to je jasno, onda cemo jos dodat e u T (promijenit zadatak)
sad dalje pise da ako je T definiran tako da su unutra svi elementi reda manjeg ili jednakog od p (a ne upravo jednaki p) da tvrdnja vrijedi
to ne kuzim, sto nije da ako su su dva elementa nekih razlicitih redova, manjih ili jednakih p (to su neki x i y) da je onda red elementa xy najmanji zajednicki visekratnik redova elementa x i elementa y? a onda to moze biti vece od p. tako da to onda ne bi bila podrupa
dobro, a ako gledamo samo elemente reda p, kako pokazemo da red elementa xy ne moze biti manji od p?
znaci, (xy)^n=e, n<p da vodi na x=y^-1, odnosno da iz x^n=(y^-1)^n mozemo zakljuciti da je x=y^-1? i dal mozemo uopce?
Neka je G Abelova grupa. Definiramo T:={a iz G: |a|=p}. Tada je T<=G.
ja nemam svoje vjezbe da se razumijemo, i nisam bila nikad na vjezbama pa desifriram fotokopije.
u prvom redu pise komentar pretpostavljam studenta cije su to biljeske (cini se da je zadatak bio za zadacu) da za p razlicit od 1 unutra nije e pa to ne moze biti podgrupa, dobro to je jasno, onda cemo jos dodat e u T (promijenit zadatak)
sad dalje pise da ako je T definiran tako da su unutra svi elementi reda manjeg ili jednakog od p (a ne upravo jednaki p) da tvrdnja vrijedi
to ne kuzim, sto nije da ako su su dva elementa nekih razlicitih redova, manjih ili jednakih p (to su neki x i y) da je onda red elementa xy najmanji zajednicki visekratnik redova elementa x i elementa y? a onda to moze biti vece od p. tako da to onda ne bi bila podrupa
dobro, a ako gledamo samo elemente reda p, kako pokazemo da red elementa xy ne moze biti manji od p?
znaci, (xy)^n=e, n<p da vodi na x=y^-1, odnosno da iz x^n=(y^-1)^n mozemo zakljuciti da je x=y^-1? i dal mozemo uopce?
_________________
Nov, još gluplji.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:59 uto, 11. 5. 2010 Naslov: Postano: 17:59 uto, 11. 5. 2010 Naslov: |
    |
|
|
[quote]Ako grupa G ima konacan broj podgrupa, tada je konačna. [/quote]
Ja bih to ovako: neka je G beskonačna. Pretpostavimo da postoji bar jedan element a iz G koji je beskonačnog reda. Tada je [latex]<a>\cong \mathbb{Z}[/latex], a jer [latex]\mathbb{Z}[/latex] ima beskonačno mnogo podgrupa, odmah ne valja.
Neka su onda svi elementi od G konačnog reda. Kada bi G imala konačno mnogo cikličkih podgrupa (ili beskonačno mnogo, ali mnoge od njih se podudaraju pa izbacimo te viškove), onda bi postojali [latex]a_1,a_2,\dots,a_k\in G[/latex] takvi da se svaki element a iz G nalazi u uniji [latex]<a_1>\cup<a_2>\cup\dots\cup<a_k>[/latex]. Ali ta unija ima konačno mnogo elemenata pa nikako ne možemo beskonačno mnogo elemenata iz G strpati u nju. Dakle, G mora imati beskonačno mnogo različitih cikličkih grupa, pa to opet ne valja.
| Citat: | | Ako grupa G ima konacan broj podgrupa, tada je konačna. |
Ja bih to ovako: neka je G beskonačna. Pretpostavimo da postoji bar jedan element a iz G koji je beskonačnog reda. Tada je 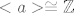 , a jer , a jer 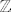 ima beskonačno mnogo podgrupa, odmah ne valja. ima beskonačno mnogo podgrupa, odmah ne valja.
Neka su onda svi elementi od G konačnog reda. Kada bi G imala konačno mnogo cikličkih podgrupa (ili beskonačno mnogo, ali mnoge od njih se podudaraju pa izbacimo te viškove), onda bi postojali  takvi da se svaki element a iz G nalazi u uniji takvi da se svaki element a iz G nalazi u uniji 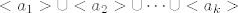 . Ali ta unija ima konačno mnogo elemenata pa nikako ne možemo beskonačno mnogo elemenata iz G strpati u nju. Dakle, G mora imati beskonačno mnogo različitih cikličkih grupa, pa to opet ne valja. . Ali ta unija ima konačno mnogo elemenata pa nikako ne možemo beskonačno mnogo elemenata iz G strpati u nju. Dakle, G mora imati beskonačno mnogo različitih cikličkih grupa, pa to opet ne valja.
_________________
The Dude Abides
Zadnja promjena: goranm; 20:47 uto, 11. 5. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:58 uto, 11. 5. 2010 Naslov: Postano: 23:58 uto, 11. 5. 2010 Naslov: |
    |
|
|
Sad da ja pitam: radi se o pokazivanju da je diedralna grupa [latex]D_n[/latex] zadana generatorima a, b i relacijama [latex]a^n=1,b^2=1,abab=1[/latex].
Uzmemo F da bude slobodna grupa generirana sa a i b, tj. F=F({a,b}) i da N bude najmanja normalna podgrupa od F koja sadrži [latex]a^n,b^2[/latex] i abab.
Neka je [latex]\pi:F\to F/N[/latex] kanonski epimorfizam. Tada je [latex]\pi(a)^n=\pi(a^n)=\pi(1)=N[/latex]. Isto tako [latex]\pi(b)^2=N, \pi(abab)=N[/latex], tj. [latex]baN=a^{-1}bN[/latex] pa F/N možemo pisati kao [latex]F/N=\{a^ib^jN:i=0,\dots,n-1,b=0,1\}[/latex], pa je [latex]|F/N|\leq 2n[/latex].
Sada tu dolazi dio koji me zbunjuje: definiramo (bar mislim da to radimo) homomorfizam [latex]f: F\to D_n[/latex] td. je f(a)=A, f(b)=B. Tu pretpostavljam da su ovi A i B generatori za [latex]D_n[/latex]? Zašto odjednom posebna oznaka za njih?
Da bi mogli napraviti faktorizaciju f kroz N mora vrijediti [latex]N\subseteq \ker{f}[/latex]. Jer je N generirana sa [latex]a^n[/latex], [latex]b^2[/latex] i abab, dovoljno je vidjeti samo kako f djeluje na njih.
Imamo
[latex]f(a^n)=(f(a))^n=A^n=1,\\
f(b^2)=(f(b))^2=B^2,\\
f(abab)=f(a)f(b)f(a)f(b)=ABAB=1[/latex]
pa je [latex]N\subseteq \ker{f}[/latex].
Sada postoji jedinstven homomorfizam [latex]\bar{f}\colon F/N\to D_n[/latex] takav da je [latex]\bar{f}(xN)=f(x)[/latex]. Jer je f epimorfizam (piše u bilješkama da je to očito, no ne vidim zašto - zato što generator preslikava u generator?), onda je i [latex]\bar{f}[/latex] epimorfizam pa je [latex]|F/N|\geq |D_n|=2n[/latex], odnosno [latex]|F/N|=2n[/latex] pa je [latex]\bar{f}[/latex] izomorfizam i onda je [latex]F/N\cong G[/latex].
Sad da ja pitam: radi se o pokazivanju da je diedralna grupa 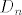 zadana generatorima a, b i relacijama zadana generatorima a, b i relacijama 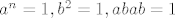 . .
Uzmemo F da bude slobodna grupa generirana sa a i b, tj. F=F({a,b}) i da N bude najmanja normalna podgrupa od F koja sadrži 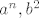 i abab. i abab.
Neka je 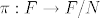 kanonski epimorfizam. Tada je kanonski epimorfizam. Tada je 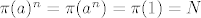 . Isto tako . Isto tako 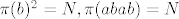 , tj. , tj. 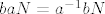 pa F/N možemo pisati kao pa F/N možemo pisati kao 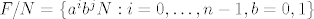 , pa je , pa je 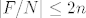 . .
Sada tu dolazi dio koji me zbunjuje: definiramo (bar mislim da to radimo) homomorfizam 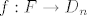 td. je f(a)=A, f(b)=B. Tu pretpostavljam da su ovi A i B generatori za td. je f(a)=A, f(b)=B. Tu pretpostavljam da su ovi A i B generatori za 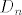 ? Zašto odjednom posebna oznaka za njih? ? Zašto odjednom posebna oznaka za njih?
Da bi mogli napraviti faktorizaciju f kroz N mora vrijediti 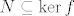 . Jer je N generirana sa . Jer je N generirana sa 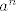 , , 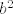 i abab, dovoljno je vidjeti samo kako f djeluje na njih. i abab, dovoljno je vidjeti samo kako f djeluje na njih.
Imamo
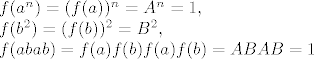
pa je 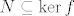 . .
Sada postoji jedinstven homomorfizam 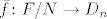 takav da je takav da je 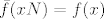 . Jer je f epimorfizam (piše u bilješkama da je to očito, no ne vidim zašto - zato što generator preslikava u generator?), onda je i . Jer je f epimorfizam (piše u bilješkama da je to očito, no ne vidim zašto - zato što generator preslikava u generator?), onda je i 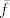 epimorfizam pa je epimorfizam pa je 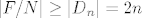 , odnosno , odnosno 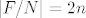 pa je pa je 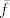 izomorfizam i onda je izomorfizam i onda je 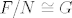 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
 Postano: 19:40 sri, 12. 5. 2010 Naslov: Postano: 19:40 sri, 12. 5. 2010 Naslov: |
    |
|
|
[quote="rafaelm"]
U takvim zadacima često je koristan Van Dyckov teorem (8.5 u Hungyju)[/quote]
9.5
prvo sam pogledala 8.5 i mislila da sam potpuno poludila :lol:
ajmeee ove vjezbe iz algebre, bas mi se place :sam:
[size=9][color=#999999]Added after 21 minutes:[/color][/size]
rafaelm, ti izgleda razumijes, oces doc sutra kod mene doma? da mi malo objasnis? ja nista ne razumijem, jos sam se ful jako udarila u glavu ujutro i tko zna koliko je tom prigodom mozdanih stanica odumrlo :glavobolja:
postavila bi ovdje konkretna pitanja, ali nisam uspjela doci do tog nivoa razumijevanja gradiva. uz velike poteskoce nazirem sto bi to bila slobodna grupa, ali ove biljeske iz kojih ucim su ko jedna velika namjestaljka nekog tko ne zeli da drugi shvate o cemu je rijec :fuj:
| rafaelm (napisa): |
U takvim zadacima često je koristan Van Dyckov teorem (8.5 u Hungyju) |
9.5
prvo sam pogledala 8.5 i mislila da sam potpuno poludila 
ajmeee ove vjezbe iz algebre, bas mi se place 
Added after 21 minutes:
rafaelm, ti izgleda razumijes, oces doc sutra kod mene doma? da mi malo objasnis? ja nista ne razumijem, jos sam se ful jako udarila u glavu ujutro i tko zna koliko je tom prigodom mozdanih stanica odumrlo 
postavila bi ovdje konkretna pitanja, ali nisam uspjela doci do tog nivoa razumijevanja gradiva. uz velike poteskoce nazirem sto bi to bila slobodna grupa, ali ove biljeske iz kojih ucim su ko jedna velika namjestaljka nekog tko ne zeli da drugi shvate o cemu je rijec 
_________________
Nov, još gluplji.
|
|
| [Vrh] |
|
|







