| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
 Postano: 14:59 ned, 16. 5. 2010 Naslov: Postano: 14:59 ned, 16. 5. 2010 Naslov: |
    |
|
|
Dali može netko objasniti, kako se određuje koja će se funkcija uzet kada se računa volumen nekog tijela. Npr.kada smo računali volumen stošca uželi smo da pravac p rotira oko x-osi,ja bi tu sigurno uzela da trokut čiav rotira,šta se ne dobije samo plaš kadaa samp pravcac rotira,a za kuglu smo rekli kao da rotira polukružnica,a uzeli smo funkciju za čitav krug?
Dali može netko objasniti, kako se određuje koja će se funkcija uzet kada se računa volumen nekog tijela. Npr.kada smo računali volumen stošca uželi smo da pravac p rotira oko x-osi,ja bi tu sigurno uzela da trokut čiav rotira,šta se ne dobije samo plaš kadaa samp pravcac rotira,a za kuglu smo rekli kao da rotira polukružnica,a uzeli smo funkciju za čitav krug?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:30 ned, 16. 5. 2010 Naslov: Postano: 17:30 ned, 16. 5. 2010 Naslov: |
    |
|
|
[quote="pajopatak"]...,ja bi tu sigurno uzela da trokut čiav rotira,...,a uzeli smo funkciju za čitav krug?[/quote]
Što bi trebala biti "funkcija za trokut/krug"? :?
Ako misliš na nešto u stilu [latex]y \leq x[/latex] i [latex]x^2 + y^2 \leq 1[/latex], to nisu funkcije. :)
Slažem se da se rotacijom dužine i polukružnice dobiva samo površina ([size=9]ploština je vjerojatno bolja riječ[/size]) bez volumena. Fora je u tome što formula [latex]\pi \int \limits_a^b f(x)^2 \, dx[/latex] ne računa volumen površine koja nastaje rotacijom krivulje oko x-osi, nego volumen tijela nastalog rotacijom površine ispod grafa funkcije.
Doista, intutivni dokaz formule bi išao tako da zbrajamo volumene sve manjih i manjih diskova. Preciznije, neka je [latex]\Delta = \{a = x_0 < x_1 < \ldots < x_n = b\}[/latex] ekvidistantna subdivizija segmenta [latex][a, b][/latex] i označimo [latex]\Delta x = x_i - x_{i-1}[/latex]. Pretpostavimo da je funkcija "dovoljno lijepa", te aproksimirajmo da rotacijom površine ispod grafa funkcije na segmentu [latex][x_{i-1}, x_i][/latex] nastaje disk volumena [latex]f(x_i)^2 \pi \Delta x[/latex]. Tada je [latex]V \approx \sum_{i = 1}^n f(x_i)^2 \pi \Delta x[/latex]. Kada pustimo n u beskonačno, to se magično pretvara u [latex]V = \int \limits_a^b f(x)^2 \pi \, dx[/latex]. :D
Ima li pitanja? :D
| pajopatak (napisa): | | ...,ja bi tu sigurno uzela da trokut čiav rotira,...,a uzeli smo funkciju za čitav krug? |
Što bi trebala biti "funkcija za trokut/krug"? 
Ako misliš na nešto u stilu 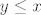 i i 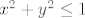 , to nisu funkcije. , to nisu funkcije. 
Slažem se da se rotacijom dužine i polukružnice dobiva samo površina (ploština je vjerojatno bolja riječ) bez volumena. Fora je u tome što formula 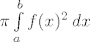 ne računa volumen površine koja nastaje rotacijom krivulje oko x-osi, nego volumen tijela nastalog rotacijom površine ispod grafa funkcije. ne računa volumen površine koja nastaje rotacijom krivulje oko x-osi, nego volumen tijela nastalog rotacijom površine ispod grafa funkcije.
Doista, intutivni dokaz formule bi išao tako da zbrajamo volumene sve manjih i manjih diskova. Preciznije, neka je 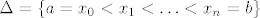 ekvidistantna subdivizija segmenta ekvidistantna subdivizija segmenta 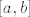 i označimo i označimo 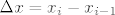 . Pretpostavimo da je funkcija "dovoljno lijepa", te aproksimirajmo da rotacijom površine ispod grafa funkcije na segmentu . Pretpostavimo da je funkcija "dovoljno lijepa", te aproksimirajmo da rotacijom površine ispod grafa funkcije na segmentu 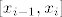 nastaje disk volumena nastaje disk volumena 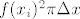 . Tada je . Tada je 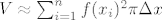 . Kada pustimo n u beskonačno, to se magično pretvara u . Kada pustimo n u beskonačno, to se magično pretvara u 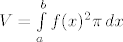 . . 
Ima li pitanja? 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
derle
Forumaš(ica)


Pridružen/a: 28. 05. 2005. (17:53:46)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
derle
Forumaš(ica)


Pridružen/a: 28. 05. 2005. (17:53:46)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
štangica
Forumaš(ica)
Pridružen/a: 19. 03. 2010. (17:18:17)
Postovi: (4C)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:44 sri, 19. 5. 2010 Naslov: Postano: 21:44 sri, 19. 5. 2010 Naslov: |
    |
|
|
[quote="niveus"]Odrediti površinu lika koji se nalazi unutar kružnice r=3cosß ali izvan kardioide r=1+cosß?[/quote]
Vjerojatno te zanima postupak, jer je rješenje zapisano u skripti. Iz [url=http://www.wolframalpha.com/input/?i=PolarPlot%28{3+Cos%28t%29%2C1%2BCos%28t%29}%2C{t%2C0%2C2+Pi}%29]slike[/url] se (skoro) vidi da se radi o polumjesecu. Lako se dobije da se kružnica i kardioida sijeku u kutevima oblika [latex]\pm \frac{\pi}{3} + 2 k \pi[/latex]. Zbog simetričnosti, stvar možemo promatrati između kuteva 0 i pi/3. Dobivamo da je [latex]\displaystyle P = 2 \left( \frac{1}{2} \int \limits_0^{\pi/3} 9 \cos^2 \varphi \, d\varphi - \frac{1}{2} \int \limits_0^{\pi/3} (1 + \cos \varphi)^2 \, d\varphi \right) = \ldots = \pi[/latex].
[quote="štangica"]jel može netko reći koliko mu je ispao 1. pod c iz zadaće?[/quote]
[size=18]1[/size]
[quote="štangica"]koja je ideja za 2. pod c?[/quote]
Za integral kod 1 se odmah vidi da konvergira ([size=7]postoji limes zdesna u 1 jednak 1[/size]). Za integral kod +beskonačno se stvari kompliciraju. Preporučam [size=7]integrirati od e do +beskonačno, dvaput parcijalno integrirati tako da integrira trig. fja., uzeti apsolutnu vrijednost, maknuti sinus, pa ograničiti ln x odozdo s 1[/size].
| niveus (napisa): | | Odrediti površinu lika koji se nalazi unutar kružnice r=3cosß ali izvan kardioide r=1+cosß? |
Vjerojatno te zanima postupak, jer je rješenje zapisano u skripti. Iz slike se (skoro) vidi da se radi o polumjesecu. Lako se dobije da se kružnica i kardioida sijeku u kutevima oblika  . Zbog simetričnosti, stvar možemo promatrati između kuteva 0 i pi/3. Dobivamo da je . Zbog simetričnosti, stvar možemo promatrati između kuteva 0 i pi/3. Dobivamo da je 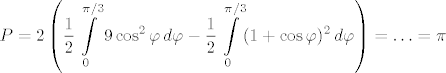 . .
| štangica (napisa): | | jel može netko reći koliko mu je ispao 1. pod c iz zadaće? |
1
| štangica (napisa): | | koja je ideja za 2. pod c? |
Za integral kod 1 se odmah vidi da konvergira (postoji limes zdesna u 1 jednak 1). Za integral kod +beskonačno se stvari kompliciraju. Preporučam integrirati od e do +beskonačno, dvaput parcijalno integrirati tako da integrira trig. fja., uzeti apsolutnu vrijednost, maknuti sinus, pa ograničiti ln x odozdo s 1.
|
|
| [Vrh] |
|
štangica
Forumaš(ica)
Pridružen/a: 19. 03. 2010. (17:18:17)
Postovi: (4C)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
|














