| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 10:58 sub, 29. 5. 2010 Naslov: Postano: 10:58 sub, 29. 5. 2010 Naslov: |
    |
|
|
[quote="michelangelo"]http://web.math.hr/nastava/la/kolokviji/08_09/kol2.pdf
može se netko pozabavit petim zadatkom ako nije problem? :D[/quote]
a) d(A) = dim(V) - r(A) = dim(V) - (dim(V) - d(A*)) = d(A*)
b) (=>)
Neka je A*Ax=0.
0 = <A*Ax,y> , za svaki y iz V
Specijalno je 0 = <A*Ax,x> = <Ax,Ax> => Ax=0.
(<=)
Ax = 0 => A*Ax = 0.
c) Lako slijedi iz a) , b)
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
@smajl
U zadatku ti je zadan skalarni produkt, sve se računa isto ko i obično samo što ovdje imaš matrice pa je zapis malo čudan, npr. norma se računa kao
korijen(tr(AA*)) itd.
Prva matrica izgleda ovako:
4 2i
4 0 puta 1/korijen(34)
I tako dalje..
Jel sad jasnije ? :D
| michelangelo (napisa): | http://web.math.hr/nastava/la/kolokviji/08_09/kol2.pdf
može se netko pozabavit petim zadatkom ako nije problem?  |
a) d(A) = dim(V) - r(A) = dim(V) - (dim(V) - d(A*)) = d(A*)
b) (⇒)
Neka je A*Ax=0.
0 = <A*Ax,y> , za svaki y iz V
Specijalno je 0 = <A*Ax,x> = <Ax,Ax> ⇒ Ax=0.
(⇐)
Ax = 0 ⇒ A*Ax = 0.
c) Lako slijedi iz a) , b)
Added after 9 minutes:
@smajl
U zadatku ti je zadan skalarni produkt, sve se računa isto ko i obično samo što ovdje imaš matrice pa je zapis malo čudan, npr. norma se računa kao
korijen(tr(AA*)) itd.
Prva matrica izgleda ovako:
4 2i
4 0 puta 1/korijen(34)
I tako dalje..
Jel sad jasnije ? 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 18:28 sub, 29. 5. 2010 Naslov: Postano: 18:28 sub, 29. 5. 2010 Naslov: |
    |
|
|
Ja bi to napravio tako da bih operator A zapisao u matricu u kanonskoj bazi, iz čega se vidi i A*, pa išao množiti te dvije matrice jer znamo da za unitarne operatore vrijedi: [latex]AA^{*}=A^{*}A=I[/latex], iz čega vidiš jeli A unitaran.
Možda ima neki bolji način, ali ja ga ne znam :D
Što se tiče drugog dijela, ako je operator unitaran znaš da vrijedi [latex]A^{-1}=A^{*}[/latex] pa slijedi [latex](A^{-1})^{*}=(A^{*})^{*}=A[/latex].
Ja bi to napravio tako da bih operator A zapisao u matricu u kanonskoj bazi, iz čega se vidi i A*, pa išao množiti te dvije matrice jer znamo da za unitarne operatore vrijedi: 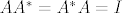 , iz čega vidiš jeli A unitaran. , iz čega vidiš jeli A unitaran.
Možda ima neki bolji način, ali ja ga ne znam 
Što se tiče drugog dijela, ako je operator unitaran znaš da vrijedi 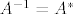 pa slijedi pa slijedi 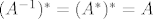 . .
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 19:00 sub, 29. 5. 2010 Naslov: Postano: 19:00 sub, 29. 5. 2010 Naslov: |
    |
|
|
[quote="Gino"][quote="Black Mamba"]Bi li ti bija problem napisat mi izgled matrice i svojstveni polinom, nemam pojma di griješim :oops:[/quote]
svojstveni polinom je valjda jasan iz svojstvenih vrijednosti, matrica je sljedeca [latex]\left(
\begin{array}{ccc}
-1 & 3 & -1 \\
3 & 5 & 3 \\
-1 & 3 & -1
\end{array}
\right)[/latex] ako si mislila na tu matricu...[/quote]
U pravu si...
Matrica mi izgleda tako, pa vjerovatno nešto glupo falivan u računu, šta neću otkrit sada...idem dalje :) (Edit: Našla grešku :D )
Može još samo pomoć oko 3- zadatka, druga grupa, ista godina...
Netko je do sad naisa rješenja,a ja uporno dobivan za skalar uz t^2 da je 0 :roll:
Hvala!
| Gino (napisa): | | Black Mamba (napisa): | Bi li ti bija problem napisat mi izgled matrice i svojstveni polinom, nemam pojma di griješim  |
svojstveni polinom je valjda jasan iz svojstvenih vrijednosti, matrica je sljedeca 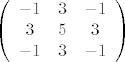 ako si mislila na tu matricu... ako si mislila na tu matricu... |
U pravu si...
Matrica mi izgleda tako, pa vjerovatno nešto glupo falivan u računu, šta neću otkrit sada...idem dalje  (Edit: Našla grešku (Edit: Našla grešku  ) )
Može još samo pomoć oko 3- zadatka, druga grupa, ista godina...
Netko je do sad naisa rješenja,a ja uporno dobivan za skalar uz t^2 da je 0 
Hvala!
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 19:45 sub, 29. 5. 2010 Naslov: Postano: 19:45 sub, 29. 5. 2010 Naslov: |
    |
|
|
[quote="Black Mamba"]
Može još samo pomoć oko 3- zadatka, druga grupa, ista godina...
Netko je do sad naisa rješenja,a ja uporno dobivan za skalar uz t^2 da je 0 :roll:
Hvala![/quote]
[latex]\displaystyle
f_1(x)=1, f_2(x)=x, f_3(x)=x^2\\
f(f_1)=1, f(f_2)=\frac{3}{2}, f(f_3)=\frac{1}{3}\\
q(x)=a + b x + c x^2\\
\left< f_1| q \right> =2 a+\frac{2 c}{3}\\
\left< f_2| q\right> =\frac{2 b}{3}\\
\left< f_3| q \right> =\frac{2 a}{3}+\frac{2 c}{5}\\
a=1/2, b=9/4, c=0
[/latex]
| Black Mamba (napisa): |
Može još samo pomoć oko 3- zadatka, druga grupa, ista godina...
Netko je do sad naisa rješenja,a ja uporno dobivan za skalar uz t^2 da je 0 
Hvala! |
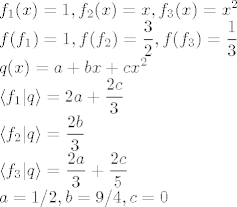
_________________
Mario Berljafa
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 20:00 sub, 29. 5. 2010 Naslov: Postano: 20:00 sub, 29. 5. 2010 Naslov: |
    |
|
|
[quote="Gino"][quote="Black Mamba"]
Može još samo pomoć oko 3- zadatka, druga grupa, ista godina...
Netko je do sad naisa rješenja,a ja uporno dobivan za skalar uz t^2 da je 0 :roll:
Hvala![/quote]
[latex]\displaystyle
f_1(x)=1, f_2(x)=x, f_3(x)=x^2\\
f(f_1)=1, f(f_2)=\frac{3}{2}, f(f_3)=\frac{1}{3}\\
q(x)=a + b x + c x^2\\
\left< f_1| q \right> =2 a+\frac{2 c}{3}\\
\left< f_2| q\right> =\frac{2 b}{3}\\
\left< f_3| q \right> =\frac{2 a}{3}+\frac{2 c}{5}\\
a=1/2, b=9/4, c=0
[/latex][/quote]
Hvala ti puno!
To su i moja rješenja :)
| Gino (napisa): | | Black Mamba (napisa): |
Može još samo pomoć oko 3- zadatka, druga grupa, ista godina...
Netko je do sad naisa rješenja,a ja uporno dobivan za skalar uz t^2 da je 0 
Hvala! |
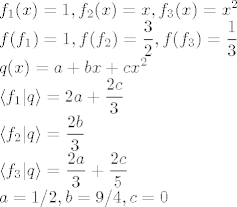 |
Hvala ti puno!
To su i moja rješenja 
|
|
| [Vrh] |
|
Gost
|
 Postano: 20:12 sub, 29. 5. 2010 Naslov: Postano: 20:12 sub, 29. 5. 2010 Naslov: |
    |
|
|
[quote="kaj"]Sv. vr. : 0,-6,3
V(0) = -1 0 1
V(-6) = 1 -4 1
V(3) = 2 1 2
Dalje valjda znaš kako ide..[/quote]
jel bi netko, molim vas, bio tako dobar i napisao kako se dalje rješava zadatak, nisam sigurna radim li dobro... :oops:
Hvala!
(to je 4. zadatak od 2009.)
| kaj (napisa): | Sv. vr. : 0,-6,3
V(0) = -1 0 1
V(-6) = 1 -4 1
V(3) = 2 1 2
Dalje valjda znaš kako ide.. |
jel bi netko, molim vas, bio tako dobar i napisao kako se dalje rješava zadatak, nisam sigurna radim li dobro... 
Hvala!
(to je 4. zadatak od 2009.)
|
|
| [Vrh] |
|
WilddWizard
Forumaš(ica)

Pridružen/a: 10. 09. 2009. (11:23:30)
Postovi: (6)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
|











