| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:41 sub, 12. 6. 2010 Naslov: Postano: 13:41 sub, 12. 6. 2010 Naslov: |
    |
|
|
Inace, kad su vec zadane dvije jednadzbe preskocis prvi korak.
1) Treba nam jos jedna jednadzba, i obicno prolazi npr [latex]B_n=A_{n-1} \forall n[/latex]
Sad se prva jednadzba moze pisati kao
[latex]A_n=3A_{n-1}+B_{n-1}[/latex]
A imamo i drugu, [latex]B_n=A_{n-1}[/latex]
2) Taj sustav od dvije jednadzbe zapisemo matricno, u ovom konkretnom slucaju:
[latex]\left(\begin{array}&A_n\\B_n\end{array}\right)=\left(\begin{array}&3 \ 1 \\ 1\ 0 \end{array}\right)\left(\begin{array}&A_{n-1}\\B_{n-1}\end{array}\right)\forall n[/latex]
3) Ako skoroz lijevu matricu oznacimo s [latex]X_n[/latex], skroz desnu s [latex]X_{n-1}[/latex], a srednju s C, onda je ocito [latex]X_n=C^{n-1}X_1[/latex] Nama je poznato sto se nalazi u [latex]X_1 [/latex] (to su A1, B1=A0), pa je sad ocito da samo trebamo potencirati matricu C, a to radimo standradno, dijagonalizacijom (na kraju, kad dobijemo C^n, uvrstimo A0 i A1 i samo izmnozimo matrice)
Inace, kad su vec zadane dvije jednadzbe preskocis prvi korak.
1) Treba nam jos jedna jednadzba, i obicno prolazi npr 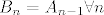
Sad se prva jednadzba moze pisati kao
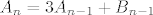
A imamo i drugu, 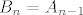
2) Taj sustav od dvije jednadzbe zapisemo matricno, u ovom konkretnom slucaju:
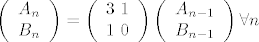
3) Ako skoroz lijevu matricu oznacimo s 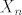 , skroz desnu s , skroz desnu s 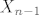 , a srednju s C, onda je ocito , a srednju s C, onda je ocito 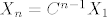 Nama je poznato sto se nalazi u Nama je poznato sto se nalazi u 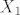 (to su A1, B1=A0), pa je sad ocito da samo trebamo potencirati matricu C, a to radimo standradno, dijagonalizacijom (na kraju, kad dobijemo C^n, uvrstimo A0 i A1 i samo izmnozimo matrice) (to su A1, B1=A0), pa je sad ocito da samo trebamo potencirati matricu C, a to radimo standradno, dijagonalizacijom (na kraju, kad dobijemo C^n, uvrstimo A0 i A1 i samo izmnozimo matrice)
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
 Postano: 14:22 ned, 13. 6. 2010 Naslov: Postano: 14:22 ned, 13. 6. 2010 Naslov: |
    |
|
|
[quote="piccola"]može li mi netko objasnit najjednostavnije kako se računaju algebarske i geometrijske kratnosti? znam da nije teško,ali nikako mi ne ide... :? :oops:[/quote]
geometrijska kratnost ti je ono koliko imas vektora u svojstvenom potprostoru od te svojstvene vrijednosti..znaci ono kad napises Va(x), ako je x sv.vrijednost..
a algebarska ti je ono na koju potenciju imas kod karakteristicnog polonoma..npr, ako ti je kar. polinom:
(x-1)^2(x-3)
onda je je algebarska kratnost od 1 jednaka 2, jer ti je tamo na kvadrat, a od 3 je 1, jel je kao na prvu..
valjda je to ok... :)
[size=9][color=#999999]Added after 58 seconds:[/color][/size]
tj, kod geom kratnosti ti je dimenzija tog svojstvenog potprostora..tako je po def..
| piccola (napisa): | može li mi netko objasnit najjednostavnije kako se računaju algebarske i geometrijske kratnosti? znam da nije teško,ali nikako mi ne ide...   |
geometrijska kratnost ti je ono koliko imas vektora u svojstvenom potprostoru od te svojstvene vrijednosti..znaci ono kad napises Va(x), ako je x sv.vrijednost..
a algebarska ti je ono na koju potenciju imas kod karakteristicnog polonoma..npr, ako ti je kar. polinom:
(x-1)^2(x-3)
onda je je algebarska kratnost od 1 jednaka 2, jer ti je tamo na kvadrat, a od 3 je 1, jel je kao na prvu..
valjda je to ok... 
Added after 58 seconds:
tj, kod geom kratnosti ti je dimenzija tog svojstvenog potprostora..tako je po def..
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
|







