Usmeni

[cvrcak2]

evo ja sam danas odgovarala! prof je bio skroz ok, spreman je pricekati ako trebas vremena da se skoncentriras ili da se prisjetis neceg. ako vidi da nesto znas, a zbunjen si, malo se potrudi da ti pomogne i navede te. doduse, danas su bili ljudi s visokim brojem bodova pa je tako i teklo . otprilike smo po 10-15 min bili unutra, ulazi jedno po jedno. ocjene su, dok sam ja bila na faksu, bile 4 i 5. pita sve, od definicija do teorema, propozicija, lema i dokaza, ne vrijedi nista preskakati u ucenju (ako je izvedivo ). neka od pitanja kojih se sjecam: sustav izvodnica, dokaz da je prikaz vektora v iz V jedinstven ako je skup baza, dokaz da je broj elemenata u skupu koji je sustav izv veci ili jednak od broja elem skupa koji je lin nezavisan, dokaz da su dvije baze jedankobrojne, nesto malo o dimenziji i napisati jednu bazu kojoj je dimenzija npr. 7, def ranga, vezu ranga i rjesivosti sustava jednadzbe, inverz, dokaz da je inverz od matrice A jedinstven, def vektorskog prostora i tako...ne sjecam se vise, ali nista strasno, sve pise u biljeznici. ne morate se bojati, mislim da i ako ne znate nesto, prof nije takav da ce vas izblamirati (barem se meni tako cinilo). i da, jedan kolega je zapisivao pitanja pa ce ih mozda on sve napisati tu... Sretno!

_________________
Čovjek je poput razlomka čiji je brojnik ono što jest, a nazivnik ono što misli o sebi. Što je nazivnik veći, razlomak je manji.

[ante003]

Pitanja su bila sljedeca :
Definicija ranga m-ce
veza ranga matrice sa rj sustava
C.Cappeli tm - dokaz
definicija potprostora v.p-a
binarna operacija
definicija inverzne matrice , uvjeti i svojstva
dokaz da postoji samo jedan inverz
definicija skupa izvodnica
definicija baze
definicija dimenzije vektorskog prostora
dokaz jednakobrojnosti baza
Objasnit kanonski oblik matrice i cemu sluzi
zasto se rang m-ce ne mjenja el. transformacijama - dokaz
svojstva determinanti
povezivanje homogenog i nehomogenog sustava
definicija konacnogeneriranog i konacnodimenzijalnog v.p-a i veza izmedu njih
suma dva vektorskih potprostora te dokaz formule dim(L+M)=dimL...
kada su dva sustava ekvivalentna
zasto su zanimljivi ekvivalentni sustavi
B. Cauchyev tm - dokaz
definicija ortogonalne matrice
definicija direktnog komplementa i da li uvjek postoji
rang matrice te zasto nije veci od m i n
mnozenje matrica, svojstva te malo o mnozenju pa sve to transponirano i na inverz
metode za izracunavanje inverza


kao sto je kolegica napisala u postu iznad, profesor nije strasan ( makar tako svi pricaju i onda se kolegice tresu ko sibe na vodi i nemogu dvije recenice normalno srocit )
sve u svemu, nista strasno
rezultat je danas bio - 11:1 za studente ( jedna osoba mora ponovno doc. ona je bila jedna od siba )
samo se opustite i sve ce bit dobro

P.S. nadam se da sam smio stavit pitanja na forum.

_________________
Ako ste previše otvorenog uma, ispast će vam mozak
------------------------------------------------------
Racunalo bez Windowsa je kao riba bez bicikla

[teapot]

sretno svima!!!

[BeeBee]

ja sam jučer odgovarala,dobila sam 4. Profesor me nije pitao ništa što nismo radili. Pitao me o inverznoj matrici i neka podpitanja o tome i navodi te na ogdovor, pomaže, stvarno je bio sasvim ok. Barem meni

[Gost]

jel mi moze netko samo objasniti drugi slucaj dokaza za formulu sume potprostora ? kada je presjek >=1
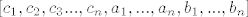je tada unija M,L i presjeka. kako bi isao postupak da ga dovedem do baze.
tenx a lot

[Gost]

c ide do p a ne do n tu fulao

[Anna Lee]

Jel postoji sansa da usmeni za nas koji idemo na popravni bude vec u cetvrtak?
A petak je neradni, jelda?

_________________
"The tooth fairy teaches children that they can sell body parts for money."

[buba]

[Juraj Siftar]

Za četvrtak su termini usmenih većinom "rasprodani", ali ako je
nekom s popravnog baš stalo odgovarati u četvrtak, možemo
to riješiti.


Nadam se da će rezultati popravnog kolokvija biti u četvrtak, za
ranije (to jest, već u srijedu) ne mogu obećati, jer zbog usmenih
ispita neću stići ispravljati kolokvije odmah nakon završetka.


J. Šiftar

[jackass9]

imam jedno pitanje na koje nemogu nać odgovor...

koja je veza između konačno generiranog i konačno dimenzionalnog vektorskog prostora?

[Buga.]

[Juraj Siftar]

Konačnodimenzionalni je (trivijalno) i konačno generiran,
jer čim ima (konačnu) bazu time ima i konačni skup izvodnica.

Obrnuto, ako prostor ima konačni skup izvodnica onda se taj
može reducirati do baze (bitno je da je konačan) pa je stoga i
konačnodimenzionalan.

(Trivijalna iznimka - nulprostor, on ima konačan skup izvodnica,
ali nema bazu no uzima se da mu je dimenzija 0).

Dakle, prostor je konačno generiran ako i samo ako je
konačnodimenzionalan, no na početku razlikujemo te pojmove
jer nije očito da su ekvivalentni i pojam dimenzije ima smisla
tek kad se zna da su sve baze jednakobrojne.

[jackass9]

Hvala puno Buga i hvala puno profesore

[cocco]

Imam pitanje u vezi dokaza leme koji kaze da ako je V vekt.prostor ,X lin.nezavisan podskup i S sistem izvodnica za V i ako se X sastoji od tocno n vektora onda S sadrzi barem n vektora.

e sad u dokazu smo X zapisali kao {x1,....,xn}
a za S smo pretpostavili da je konačan skup ,S={a1,...,am}
treba dokazati da je n manje ili jednako od m
uzmemo skup S1={x1,a1,....,am} (kao uređen skup)

S1 je i dalje sisem izvodnica jer nadskup od S,ali zasto je linearno zavisan kad ne vrijedi da je x1 element [S1/{x1}] ???

[Sekanta]

koliko ja znam vrijedi.
S1 je skup izvodnica i to lin. zavisan jer je x1 iz [S], a to znaci i da je iz [S/{x1}], zato postoji neki vektor u S1 koji je lin kombinacija svojih prethodnika.

[ddd]

imam jedno pitanje...

dali mi koji smo bili na popravnom imamo samo jednu priliku na usmenom,ili isto 2 kao i ostali..??????

molila bi ako neko zna,jer sutra odgovaram,i jako me strah.

[Jo]

Da li može netko tko je odgovarao prošli tjedan napisati još neka pitanja kojih se sjeća?

[Gost]

Meni je rečeno da imamo svi dvije šanse, rekla mi jedna cura koja je prošle god bila na popravnom kolokviju i svejedno mogla dvaput doći na usmeni.
samo bez straha..i sretno.

[bernhard]

[ddd]

Mi koji smo bili na popravnom, ispucali smo svoj joker za popravne t.d. mi imamo samo tu jednu jedinu priliku za prolaz.
Nauci SVE S RAZUMIJEVANJEM i bit ce ok [/quote]


aaaaa,,jos nisam ni pocela ucit