| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:00 pet, 9. 4. 2010 Naslov: Re: oscilacija i Darbouxove sume Postano: 19:00 pet, 9. 4. 2010 Naslov: Re: oscilacija i Darbouxove sume |
    |
|
|
[quote="tidus"]
2. Neznam kako bi ovo sve napisao, pa evo link [7. zadatak pod a)] :
http://web.math.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf[/quote]
Po definiciji ideš :D
Evo ja ću npr donju Darbouxovu sumu, gornja ide slično:
[latex]s=\sum_{i=0}^{n}\sum_{j=0}^{n} minf(Pij)\cdot p(Pij)[/latex]
gdje je minf minimum fje f na Pij, a Pij i-ti kvadratić u subdiviziji.
Kvadratići će bit [latex]P_{ij} = [\frac{i}{n}, \frac{i+1}{n}] \times [\frac{j}{n},\frac{j+1}{n}][/latex] za i=0,..,n ; j=0,...,n i fja f(x,y)=x će minimalna biti na lijevom rubu, tj minf(Pij)=i/n.
P(Pij) = 1/n^2
i sada je
[latex]s=\sum_{i=0}^{n}\sum_{j=0}^{n} \frac{i}{n} \cdot \frac{1}{n^2} = \frac{1}{n^3} \cdot \frac{n(n+1)}{2} \cdot (n+1) = \frac{n^2+2n+1}{2n^2}[/latex]
(onaj n+1 dođe od ove sume po j, pošto nema j nigdje, ostane suma jedinica, i to n+1 komad)
Dobili smo donju D. sumu, analogno se dobije gornja (samo se gleda maximum fje a Pij, to je onda desni rub).
Fja je integrabilna ako je [latex]lim_n s(n) = lim_n S(n)[/latex]
Za provjeru, možeš izračunat [latex]\int_0^1 \int_0^1 xdxdy[/latex] pa vidjet dal dobiješ isti onaj limes (1/2)
Po definiciji ideš 
Evo ja ću npr donju Darbouxovu sumu, gornja ide slično:
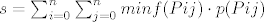
gdje je minf minimum fje f na Pij, a Pij i-ti kvadratić u subdiviziji.
Kvadratići će bit 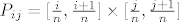 za i=0,..,n ; j=0,...,n i fja f(x,y)=x će minimalna biti na lijevom rubu, tj minf(Pij)=i/n. za i=0,..,n ; j=0,...,n i fja f(x,y)=x će minimalna biti na lijevom rubu, tj minf(Pij)=i/n.
P(Pij) = 1/n^2
i sada je
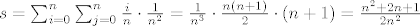
(onaj n+1 dođe od ove sume po j, pošto nema j nigdje, ostane suma jedinica, i to n+1 komad)
Dobili smo donju D. sumu, analogno se dobije gornja (samo se gleda maximum fje a Pij, to je onda desni rub).
Fja je integrabilna ako je 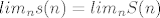
Za provjeru, možeš izračunat 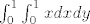 pa vidjet dal dobiješ isti onaj limes (1/2) pa vidjet dal dobiješ isti onaj limes (1/2)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
assssssss
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
čungalunga
Forumaš(ica)


Pridružen/a: 25. 11. 2009. (20:50:12)
Postovi: (4C)16
Spol: 
Lokacija: varaždin/zagreb
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 9:58 sri, 16. 6. 2010 Naslov: Postano: 9:58 sri, 16. 6. 2010 Naslov: |
    |
|
|
[quote="čungalunga"]mene zanima oscilacija kak se računa, npr u primjeru 6.
http://web.math.hr/nastava/difraf/int/2008-09/kolokvij1.pdf[/quote]
pogledaj skup C: to ti je skup svih točaka na R^2 takvih da su od ishodišta udaljene za >= 1 i < 2, tj. to ti je kružni vijenac koji ne sadrži kružnicu r = 2 a sadrži kružnicu r = 1.
skup D ti je skup: krug radijusa 1 koji sadrži svoj rub ( kružnicu radijusa 1 ).
Kad pogledaš presjek ta 2 skupa dobiješ kružnicu radijusa 1 ( x^2 + y^2 = 1 ).
tebe zanima oscilacija funkcije:
[latex]f = 2X_C - X_D[/latex]
sad pogledaj funkcije:
[latex]X_D[/latex] - ta funkcija je 1 za sve točke koje su unutar skupa D, inače 0, isto vrijedi za funkciju [latex]X_C[/latex] samo što gledaš skup C.
Sad pogledaj kak f djeluje na R^2.
prvo: f na skupu D bez kružnice radijusa 1 postiže vrijednost -1, na kružnici radijusa 1 postiže vrijednost 1, na skupu C bez kružnice radijusa 1 postiže 2, a na svim ostalim točkama od r^2 postiže 0.
kako je oscilacija u točki c:
[latex]\displaystyle{ O(f,c) = inf_{U} sup_{ x_1,x_2 \in U \cap A }| f(x_1) - f(x_2)| }[/latex]
gdje je U bilo koja okolina točke c. Što sad treba raditi: vidiš kako djeluje f na različitim područjima: umeš prvo točku c iz R^2 \ { C U D }. kako smo rekli tam funkcija f postiže vrijednost 0. Sad za svaku okolinu moraš gledat najveću vrijednost. Ako ti je okolina ima prazan presjek sa skupom: C U D onda ti za svake dvije točke funkcija postiže vrijednost 0 pa je i onaj supremum iz definicije uvijek jednak 0. ako ti okolina U siječe skup C, ali ne i skup D tada funkcija f u nekoj točki postiže u vrijednost 2( točke iz skupa C ), a u nekim 0 ( R^2\{C U D} ) pa ti je onaj supremum 2, sad isto tako možeš gledat da ti okolina siječe i D ( onda siječe i C ) pa gledaš tu najveću moguću vrijednost. vidiš da ti funkcija u skupu D postiže vrijednost -1, a u skupu C 2, pa ti je onaj supremum jednak 3. Sad su pokriveni svi mogći slučajevi ako je c iz R^2\{ C U D }
i vidiš da za različite okoline dobivaš vrijednosti onih supremuma: 0, 2, 3. sada gledaš infinum tih vrijednosti i vidiš da je taj infinum jednak 0, tj.
[latex]O(f,c) = 0, c \in \mathbb{R}^2\backslash \{ C \cup D \}[/latex]
isto tako dobiješ da je:
[latex]O(f,c) = 0, c \in C[/latex]
[latex]O(f,c) = 0, c \in D[/latex]
i
[latex]O(f,c) = 3, c \in C\cap D[/latex]
pogledaj skup C: to ti je skup svih točaka na R^2 takvih da su od ishodišta udaljene za >= 1 i < 2, tj. to ti je kružni vijenac koji ne sadrži kružnicu r = 2 a sadrži kružnicu r = 1.
skup D ti je skup: krug radijusa 1 koji sadrži svoj rub ( kružnicu radijusa 1 ).
Kad pogledaš presjek ta 2 skupa dobiješ kružnicu radijusa 1 ( x^2 + y^2 = 1 ).
tebe zanima oscilacija funkcije:
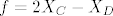
sad pogledaj funkcije:
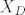 - ta funkcija je 1 za sve točke koje su unutar skupa D, inače 0, isto vrijedi za funkciju - ta funkcija je 1 za sve točke koje su unutar skupa D, inače 0, isto vrijedi za funkciju 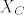 samo što gledaš skup C. samo što gledaš skup C.
Sad pogledaj kak f djeluje na R^2.
prvo: f na skupu D bez kružnice radijusa 1 postiže vrijednost -1, na kružnici radijusa 1 postiže vrijednost 1, na skupu C bez kružnice radijusa 1 postiže 2, a na svim ostalim točkama od r^2 postiže 0.
kako je oscilacija u točki c:
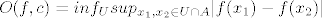
gdje je U bilo koja okolina točke c. Što sad treba raditi: vidiš kako djeluje f na različitim područjima: umeš prvo točku c iz R^2 \ { C U D }. kako smo rekli tam funkcija f postiže vrijednost 0. Sad za svaku okolinu moraš gledat najveću vrijednost. Ako ti je okolina ima prazan presjek sa skupom: C U D onda ti za svake dvije točke funkcija postiže vrijednost 0 pa je i onaj supremum iz definicije uvijek jednak 0. ako ti okolina U siječe skup C, ali ne i skup D tada funkcija f u nekoj točki postiže u vrijednost 2( točke iz skupa C ), a u nekim 0 ( R^2\{C U D} ) pa ti je onaj supremum 2, sad isto tako možeš gledat da ti okolina siječe i D ( onda siječe i C ) pa gledaš tu najveću moguću vrijednost. vidiš da ti funkcija u skupu D postiže vrijednost -1, a u skupu C 2, pa ti je onaj supremum jednak 3. Sad su pokriveni svi mogći slučajevi ako je c iz R^2\{ C U D }
i vidiš da za različite okoline dobivaš vrijednosti onih supremuma: 0, 2, 3. sada gledaš infinum tih vrijednosti i vidiš da je taj infinum jednak 0, tj.
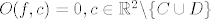
isto tako dobiješ da je:
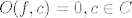
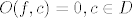
i
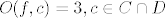
|
|
| [Vrh] |
|
čungalunga
Forumaš(ica)


Pridružen/a: 25. 11. 2009. (20:50:12)
Postovi: (4C)16
Spol: 
Lokacija: varaždin/zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 14:46 sri, 16. 6. 2010 Naslov: Postano: 14:46 sri, 16. 6. 2010 Naslov: |
    |
|
|
pa funkcija f je zadana tako:
[latex]f(x) = 2X_C - X_D[/latex], tj.
s obzirom na djelovanje funkcija [latex]X_C[/latex] i [latex]X_D[/latex]
tj,
[latex]X_C(x) = 1[/latex] za [latex]x \in C[/latex] ,za sve ostale x-eve je 0
[latex]X_D(x) = 1[/latex] za [latex]x \in D[/latex] ,za sve ostale x-eve je 0
pa je:
[latex]f(x) = 2\cdot 0 - 1 = -1[/latex] za [latex]x \in D [/latex], [latex]x \notin C[/latex]
( f na skupu D bez kružnice radijusa 1 postiže vrijednost -1 )
[latex]f(x) = 2\cdot 1 - 1 = 1[/latex] za [latex]x \in C\cap D [/latex]
(na kružnici radijusa 1 postiže vrijednost 1)
[latex]f(x) = 2\cdot 1 - 0 = 2[/latex] za [latex]x \in C[/latex], [latex]x \notin D[/latex]
( na skupu C bez kružnice radijusa 1 postiže 2 )
[latex]f(x) = 2\cdot 0 - 0 = 0[/latex] za [latex]x \in \mathbb{R}^2 \backslash \{C\cup D\} [/latex]
( a na svim ostalim točkama od r^2 postiže 0. )
pa funkcija f je zadana tako:
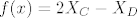 , tj. , tj.
s obzirom na djelovanje funkcija 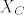 i i 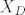
tj,
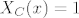 za za 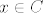 ,za sve ostale x-eve je 0 ,za sve ostale x-eve je 0
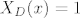 za za 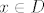 ,za sve ostale x-eve je 0 ,za sve ostale x-eve je 0
pa je:
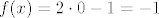 za za 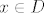 , , 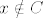
( f na skupu D bez kružnice radijusa 1 postiže vrijednost -1 )
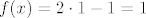 za za 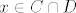
(na kružnici radijusa 1 postiže vrijednost 1)
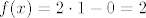 za za 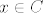 , , 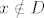
( na skupu C bez kružnice radijusa 1 postiže 2 )
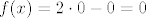 za za 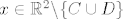
( a na svim ostalim točkama od r^2 postiže 0. )
|
|
| [Vrh] |
|
|










