| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 7:53 uto, 8. 6. 2010 Naslov: Postano: 7:53 uto, 8. 6. 2010 Naslov: |
    |
|
|
Izgubili ste [latex]-\sqrt{2}[/latex] ;)
Inače, takva jednadžba se zove bikvadratna, i rješava se supstitucijom [latex]y=x^2[/latex]. Paziti na ova rješenja s minusom, jer se radi o jednadžbi 4. stupnja i ako determinanta (ono pod korijenom, jel) nije nula, bit će četiri rješenja (u skupu kompleksnih brojeva ako je <0, u realnim ako je >0)
@tihana Imaš malo previše ako_i_samo_ako strelica :D
Izgubili ste 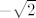 
Inače, takva jednadžba se zove bikvadratna, i rješava se supstitucijom 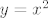 . Paziti na ova rješenja s minusom, jer se radi o jednadžbi 4. stupnja i ako determinanta (ono pod korijenom, jel) nije nula, bit će četiri rješenja (u skupu kompleksnih brojeva ako je <0, u realnim ako je >0) . Paziti na ova rješenja s minusom, jer se radi o jednadžbi 4. stupnja i ako determinanta (ono pod korijenom, jel) nije nula, bit će četiri rješenja (u skupu kompleksnih brojeva ako je <0, u realnim ako je >0)
@tihana Imaš malo previše ako_i_samo_ako strelica 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 11:37 uto, 8. 6. 2010 Naslov: Postano: 11:37 uto, 8. 6. 2010 Naslov: |
    |
|
|
ovo rijesenje od pmlia mi se cini dosta jednostavno,moje pitanje:
da li se moze ako je nesto u zagradi i onda na kvadrat, recimo [latex](1x-4)^2 =0 [/latex]-da li se moze kvadrat nad zagradom uvijek rijesiti tako da izvrsimo drugi korijen nad njom i tako se rijesimo potencije(u ovom slucaju 2 i onda dalje rijesavamo bez zagrade i potencije
To mi se cini dosta lako,samo ako je i matematicki moguce
Hvala na odgovoru
[size=9][color=#999999]Added after 26 minutes:[/color][/size]
Evo sam sam si odgovorio na svoje zadnje pitanje, to je zaista tako ,rijesio sam 10-ak slicnih zadatak na istu foru,i svi ispadaju dobro.
Ipak hvala, ovaj forum je brz i coool :D
ovo rijesenje od pmlia mi se cini dosta jednostavno,moje pitanje:
da li se moze ako je nesto u zagradi i onda na kvadrat, recimo 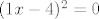 -da li se moze kvadrat nad zagradom uvijek rijesiti tako da izvrsimo drugi korijen nad njom i tako se rijesimo potencije(u ovom slucaju 2 i onda dalje rijesavamo bez zagrade i potencije -da li se moze kvadrat nad zagradom uvijek rijesiti tako da izvrsimo drugi korijen nad njom i tako se rijesimo potencije(u ovom slucaju 2 i onda dalje rijesavamo bez zagrade i potencije
To mi se cini dosta lako,samo ako je i matematicki moguce
Hvala na odgovoru
Added after 26 minutes:
Evo sam sam si odgovorio na svoje zadnje pitanje, to je zaista tako ,rijesio sam 10-ak slicnih zadatak na istu foru,i svi ispadaju dobro.
Ipak hvala, ovaj forum je brz i coool 
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:01 uto, 8. 6. 2010 Naslov: Postano: 19:01 uto, 8. 6. 2010 Naslov: |
    |
|
|
[quote="ivicasb1"]ovo rijesenje od pmlia mi se cini dosta jednostavno,moje pitanje:
da li se moze ako je nesto u zagradi i onda na kvadrat, recimo [latex](1x-4)^2 =0 [/latex]-da li se moze kvadrat nad zagradom uvijek rijesiti tako da izvrsimo drugi korijen nad njom i tako se rijesimo potencije(u ovom slucaju 2 i onda dalje rijesavamo bez zagrade i potencije
To mi se cini dosta lako,samo ako je i matematicki moguce
Hvala na odgovoru [/quote]
Možeš ako je s druge strane nula, inače na drugoj strani ide sa +-, npr:
[latex](2x+7)^2=4 \to 2x+7=\pm 2 [/latex]
| ivicasb1 (napisa): | ovo rijesenje od pmlia mi se cini dosta jednostavno,moje pitanje:
da li se moze ako je nesto u zagradi i onda na kvadrat, recimo 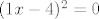 -da li se moze kvadrat nad zagradom uvijek rijesiti tako da izvrsimo drugi korijen nad njom i tako se rijesimo potencije(u ovom slucaju 2 i onda dalje rijesavamo bez zagrade i potencije -da li se moze kvadrat nad zagradom uvijek rijesiti tako da izvrsimo drugi korijen nad njom i tako se rijesimo potencije(u ovom slucaju 2 i onda dalje rijesavamo bez zagrade i potencije
To mi se cini dosta lako,samo ako je i matematicki moguce
Hvala na odgovoru |
Možeš ako je s druge strane nula, inače na drugoj strani ide sa +-, npr:
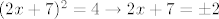
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 11:33 sub, 24. 7. 2010 Naslov: slican problem Postano: 11:33 sub, 24. 7. 2010 Naslov: slican problem |
    |
|
|
Evo imam jos jedanu slicnu situaciju, koja me zulja ( bila je u ispitu ,kao dio jednog zadatka ) pa ako mi moze netko na brzaka rijesiti, THX!
[latex]x^2+2xy+y^2= 6+y[/latex]
e iz toga moram izracunati koliki su x1 i x2 i y1 i y2
Jel se to moze svesti na oblik [latex](x+y)^2= y+6[/latex] i onda metodom pogadanja vrsiti jednakost s ljeve i desne strane!?
Na taj nacin mi ispadne (0,3) i (0,-2) Jel se moze to tako racunati?
Evo imam jos jedanu slicnu situaciju, koja me zulja ( bila je u ispitu ,kao dio jednog zadatka ) pa ako mi moze netko na brzaka rijesiti, THX!
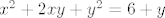
e iz toga moram izracunati koliki su x1 i x2 i y1 i y2
Jel se to moze svesti na oblik 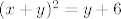 i onda metodom pogadanja vrsiti jednakost s ljeve i desne strane!? i onda metodom pogadanja vrsiti jednakost s ljeve i desne strane!?
Na taj nacin mi ispadne (0,3) i (0,-2) Jel se moze to tako racunati?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:15 sub, 24. 7. 2010 Naslov: Postano: 13:15 sub, 24. 7. 2010 Naslov: |
    |
|
|
A što su x1,x2,y1,y2? Moraju li biti nekog posebnog tipa, npr. cijeli brojevi? Postoji li neka restrikcija na izbor x1,x2,y1,y2?
Parovi (0,3) i (0,-2) su samo dva od beskonačno mnogo uređenih parova (x,y) koji zadovoljavaju [latex]x^2+2xy+y^2= 6+y[/latex]. Npr. za bilo koji
[latex]y\geq -6[/latex] postojati će pripadni x takav da je [latex]x^2+2xy+y^2= 6+y[/latex]. Tako su za y=0 rješenja također [latex](\sqrt{6},0)[/latex] i [latex](-\sqrt{6},0)[/latex].
Ima čak i beskonačno cjelobrojnih rješejna, za bilo koji [latex]n\in\mathbb{Z}[/latex],
[latex]x=-n^2+n+6\\
y=n^2-6[/latex]
zadovoljavaju jednadžbu.
A što su x1,x2,y1,y2? Moraju li biti nekog posebnog tipa, npr. cijeli brojevi? Postoji li neka restrikcija na izbor x1,x2,y1,y2?
Parovi (0,3) i (0,-2) su samo dva od beskonačno mnogo uređenih parova (x,y) koji zadovoljavaju 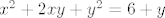 . Npr. za bilo koji . Npr. za bilo koji
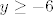 postojati će pripadni x takav da je postojati će pripadni x takav da je 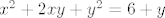 . Tako su za y=0 rješenja također . Tako su za y=0 rješenja također 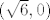 i i 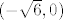 . .
Ima čak i beskonačno cjelobrojnih rješejna, za bilo koji 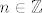 , ,
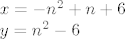
zadovoljavaju jednadžbu.
_________________
The Dude Abides
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:15 sub, 24. 7. 2010 Naslov: Postano: 18:15 sub, 24. 7. 2010 Naslov: |
    |
|
|
Sada je jasnije. :) Našao si dobar par točaka s tim da nije bilo potrebno, kako si napisao, pogađati. Točke krivulje koje sijeku y-os imaju apscisu jednaku 0, tj. x=0. Nakon što se x=0 uvrsti u [latex]x^2+2xy+y^2=6+y,[/latex] ostane [latex]y^2-y-6=0[/latex], a rješenja te kvadratne jednadžbe su 3 i -2 pa su tražene točke (0,3) i (0,-2).
Sada je jasnije.  Našao si dobar par točaka s tim da nije bilo potrebno, kako si napisao, pogađati. Točke krivulje koje sijeku y-os imaju apscisu jednaku 0, tj. x=0. Nakon što se x=0 uvrsti u Našao si dobar par točaka s tim da nije bilo potrebno, kako si napisao, pogađati. Točke krivulje koje sijeku y-os imaju apscisu jednaku 0, tj. x=0. Nakon što se x=0 uvrsti u 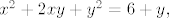 ostane ostane 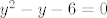 , a rješenja te kvadratne jednadžbe su 3 i -2 pa su tražene točke (0,3) i (0,-2). , a rješenja te kvadratne jednadžbe su 3 i -2 pa su tražene točke (0,3) i (0,-2).
_________________
The Dude Abides
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:14 ned, 25. 7. 2010 Naslov: Postano: 20:14 ned, 25. 7. 2010 Naslov: |
    |
|
|
Pa napisao si kako se dobiju S1 i S2, rješavanjem sustava
[latex]y=(x-2)^2\\y=-4+6x-x^2[/latex]
Npr. y iz prve jednadžbe uvrstiš u drugu i dobije se [latex](x-2)^2=-4+6x-x^2,[/latex] odnosno, nakon raspisivanja, [latex]x^2-5x+4=0.[/latex]
Rješenja te kvadratne jednadžbe su 1 i 4. Sada ta rješenja uvrstiš u jednu jednadžbu iz sustava, npr. [latex]y=(x-2)^2[/latex] jer je jednostavnija. Za x=1 je y=1, a za x=4, je y=4 pa su sjecišta tih krivulja (1,1) i (4,4).
Pa napisao si kako se dobiju S1 i S2, rješavanjem sustava
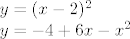
Npr. y iz prve jednadžbe uvrstiš u drugu i dobije se 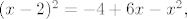 odnosno, nakon raspisivanja, odnosno, nakon raspisivanja, 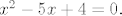
Rješenja te kvadratne jednadžbe su 1 i 4. Sada ta rješenja uvrstiš u jednu jednadžbu iz sustava, npr. 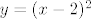 jer je jednostavnija. Za x=1 je y=1, a za x=4, je y=4 pa su sjecišta tih krivulja (1,1) i (4,4). jer je jednostavnija. Za x=1 je y=1, a za x=4, je y=4 pa su sjecišta tih krivulja (1,1) i (4,4).
_________________
The Dude Abides
|
|
| [Vrh] |
|
ante003
Forumaš(ica)


Pridružen/a: 13. 10. 2008. (17:45:10)
Postovi: (3C5)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 17:54 pon, 26. 7. 2010 Naslov: Postano: 17:54 pon, 26. 7. 2010 Naslov: |
    |
|
|
Gorane i Ante , hvala! Evo rijesio sam jos tri slicna zadatka na taj nacin, u biti laganini, samo dok skuzis :o
Evo sad sam kod vjezbanja naisao na jos jedan zadatak koji ne mogu na taj nacin rijesiti, pa ako vi znate bilo bi cooool
Zadana je funkcija [latex]x^2-xy+2y^2=28[/latex]
Kaze: Izracunajte tocke presjeka zadane funkcije i pravca y=2x
(Rj. je T1(2,4) i T2(-2,-4))
Kako to izracunati?
Nadam se da postoji jednostavnije rijesenje od crtanja grafa funkcije i pravca i onda gledanja gdje se sjeku :shock:
Hvala na odgovorima
[size=9][color=#999999]Added after 37 minutes:[/color][/size]
A joj :D
Ma uspio sam ga rijesiti,
pa samo se umjesto x u jednadzbi uvrsti 2x i onda se razrijesi jednadzba i to je to!
Ipak hvala!
pöööööööööözdrav
Gorane i Ante , hvala! Evo rijesio sam jos tri slicna zadatka na taj nacin, u biti laganini, samo dok skuzis 
Evo sad sam kod vjezbanja naisao na jos jedan zadatak koji ne mogu na taj nacin rijesiti, pa ako vi znate bilo bi cooool
Zadana je funkcija 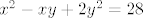
Kaze: Izracunajte tocke presjeka zadane funkcije i pravca y=2x
(Rj. je T1(2,4) i T2(-2,-4))
Kako to izracunati?
Nadam se da postoji jednostavnije rijesenje od crtanja grafa funkcije i pravca i onda gledanja gdje se sjeku 
Hvala na odgovorima
Added after 37 minutes:
A joj 
Ma uspio sam ga rijesiti,
pa samo se umjesto x u jednadzbi uvrsti 2x i onda se razrijesi jednadzba i to je to!
Ipak hvala!
pöööööööööözdrav
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
|















