|
Za razliku od zadataka koji su cesto shablonski (barem ovi jednostavniji), kod dokaza nema shablona. Osnovno je da krenes od onoga sto znas i gradis prema onome sto ti treba.
Gore je trebalo pokazati da je
[latex]f(A \cup B) \subseteq f(A) \cup f(B)[/latex]
Znas li nesto reci o [latex]f(A \cup B)[/latex]?
Vjerojatno ne. Ali [b]znas[/b] sto je to podskup, pa znas da ti treba (po definiciji podskupa):
[latex]\forall y:\ y \in f(A \cup B) \Rightarrow y \in f(A) \cup f(B)[/latex]
Na hrvatskom:
[i]Za svaki y iz f(AUB), mora biti i y iz f(A)Uf(B).[/i]
Ili, drugacije receno:
[i]Ako imamo y iz f(AUB), onda taj y mora biti i iz f(A)Uf(B).[/i]
To [b]zelimo pokazati[/b].
Kako cemo to pokazati?
Krenut cemo od ovog drugog prijevoda na hrvatski ([i]Ako imamo y iz f(AUB), onda taj y mora biti i iz f(A)Uf(B).[/i]):
Pretpostavimo da imamo neki [i]y[/i] koji zadovoljava trazeno, dakle
[latex]y \in f(A \cup B)[/latex]
Sto mozemo zakljuciti? Posto je [i]y[/i] iz slike skupa AUB, zakljucujemo da [i]postoji x iz tog skupa koji se preslikava u taj y[/i] ili, formalno zapisano:
[latex]\exists x \in A \cup B:\ x = f(y)[/latex] za taj odredjeni [latex]y \in f(A \cup B)[/latex]
Prema definiciji unije, [i]svaki element unije je ujedno i element barem jednog od skupova koje spajamo unijom[/i], odnosno formalno
[latex]x \in A \cup B \quad \Rightarrow \quad x \in A \ \rm{ili} \ x \in B[/latex]
(naravno, moze biti i oboje, jer "ili" ne iskljucuje tu mogucnost)
I sada imamo da je [i]x[/i] iz jednog od dva skupa. Odakle je onda slika od [i]x[/i]? Pa,
1. ako je [latex]x \in A[/latex], onda je [latex]y = f(x) \in f(A)[/latex], a
2. ako je [latex]x \in B[/latex], onda je [latex]y = f(x) \in f(B)[/latex].
Posto za [i]x[/i] ne znamo nista vise nego da je iz A [b]ili[/b] i z B, onda imamo da je y iz f(A) [b]ili[/b] iz f(B), tj.
[latex]y = f(x) \in f(A) \ \rm{ili} \ y = f(x) \in f(B)[/latex].
No, po definiciji unije, to znaci da je
[latex]y = f(x) \in f(A) \cup f(B)[/latex],
sto smo i htjeli pokazati.
Za [i]y[/i] smo pretpostavili samo da je iz f(AUB), bez ikakvih drugih ogranicenja, i onda smo provukli zakljucivanje (bez dodatnih pretpostavki). To znaci da takvo zakljucivanje vrijedi za sve takve [i]y[/i], pa imamo da
[i]za svaki y iz f(AUB) vrijedi da je y iz f(A) U f(B)[/i] ili, opet, formalno zapisano:
[latex]\forall y:\ y \in f(A \cup B) \Rightarrow y \in f(A) \cup f(B)[/latex],
sto je, po definiciji podskupa, upravo ono sto smo zeljeli dokazati.
Dakle, jos jednom: gledas sto znas i raspisujes, te pokusavas odvuci u smjeru onoga sto zelis. Ako zapnes, mozda si negdje znala nesto drugo sto si mogla raspisati i tako krenuti u nekom drugom smjeru? Naravno, moguce je i da si pogrijesila.
Uputa za gornji zadatak bi glasila:
raspisi definiciju podskupa i pogledaj prasliku (to ti je ono "odakle moze biti [i]x[/i]").
Uz pretpostavku da znas sto su podskup i praslika, vjerojatno bi se sama snasla (mozda ne skroz glatko, ali uz malo muke...).
A praksom se uhodas i bude lakse.
Nadam se da je ovo pomoglo.
P.S. Za domacu zadacu pokazi da je [latex]f(A \cap B) \subseteq f(A) \cap f(B)[/latex] (bez gledanja u dokaze na ovom topicu). :D
P.P.S. Pokusaj dokazati obratne tvrdnje:
[latex]f(A \cup B) \supseteq f(A) \cup f(B)[/latex] i
[latex]f(A \cap B) \supseteq f(A) \cap f(B)[/latex].
Jedna od tih tvrdnji je tocna, a druga nije, pa bi jednu morala moci dokazati, a kod druge bi morala zapeti.
Cisto za mentalnu gimnastiku (nema direktne veze s dokazivanjem), probaj naci primjer koji pokazuju da pogresna tvrdnja zaista ne vrijedi.
Hint: protuprimjeri se obicno lako skuze iz onoga na cemu ti dokaz zapne.
Za razliku od zadataka koji su cesto shablonski (barem ovi jednostavniji), kod dokaza nema shablona. Osnovno je da krenes od onoga sto znas i gradis prema onome sto ti treba.
Gore je trebalo pokazati da je
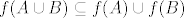
Znas li nesto reci o 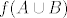 ? ?
Vjerojatno ne. Ali znas sto je to podskup, pa znas da ti treba (po definiciji podskupa):
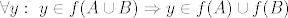
Na hrvatskom:
Za svaki y iz f(AUB), mora biti i y iz f(A)Uf(B).
Ili, drugacije receno:
Ako imamo y iz f(AUB), onda taj y mora biti i iz f(A)Uf(B).
To zelimo pokazati.
Kako cemo to pokazati?
Krenut cemo od ovog drugog prijevoda na hrvatski (Ako imamo y iz f(AUB), onda taj y mora biti i iz f(A)Uf(B).):
Pretpostavimo da imamo neki y koji zadovoljava trazeno, dakle
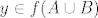
Sto mozemo zakljuciti? Posto je y iz slike skupa AUB, zakljucujemo da postoji x iz tog skupa koji se preslikava u taj y ili, formalno zapisano:
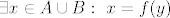 za taj odredjeni za taj odredjeni 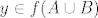
Prema definiciji unije, svaki element unije je ujedno i element barem jednog od skupova koje spajamo unijom, odnosno formalno

(naravno, moze biti i oboje, jer "ili" ne iskljucuje tu mogucnost)
I sada imamo da je x iz jednog od dva skupa. Odakle je onda slika od x? Pa,
1. ako je 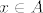 , onda je , onda je 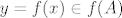 , a , a
2. ako je 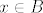 , onda je , onda je 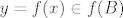 . .
Posto za x ne znamo nista vise nego da je iz A ili i z B, onda imamo da je y iz f(A) ili iz f(B), tj.
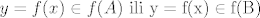 . .
No, po definiciji unije, to znaci da je
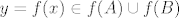 , ,
sto smo i htjeli pokazati.
Za y smo pretpostavili samo da je iz f(AUB), bez ikakvih drugih ogranicenja, i onda smo provukli zakljucivanje (bez dodatnih pretpostavki). To znaci da takvo zakljucivanje vrijedi za sve takve y, pa imamo da
za svaki y iz f(AUB) vrijedi da je y iz f(A) U f(B) ili, opet, formalno zapisano:
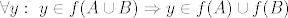 , ,
sto je, po definiciji podskupa, upravo ono sto smo zeljeli dokazati.
Dakle, jos jednom: gledas sto znas i raspisujes, te pokusavas odvuci u smjeru onoga sto zelis. Ako zapnes, mozda si negdje znala nesto drugo sto si mogla raspisati i tako krenuti u nekom drugom smjeru? Naravno, moguce je i da si pogrijesila.
Uputa za gornji zadatak bi glasila:
raspisi definiciju podskupa i pogledaj prasliku (to ti je ono "odakle moze biti x").
Uz pretpostavku da znas sto su podskup i praslika, vjerojatno bi se sama snasla (mozda ne skroz glatko, ali uz malo muke...).
A praksom se uhodas i bude lakse.
Nadam se da je ovo pomoglo.
P.S. Za domacu zadacu pokazi da je 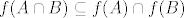 (bez gledanja u dokaze na ovom topicu). (bez gledanja u dokaze na ovom topicu). 
P.P.S. Pokusaj dokazati obratne tvrdnje:
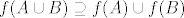 i i
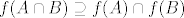 . .
Jedna od tih tvrdnji je tocna, a druga nije, pa bi jednu morala moci dokazati, a kod druge bi morala zapeti.
Cisto za mentalnu gimnastiku (nema direktne veze s dokazivanjem), probaj naci primjer koji pokazuju da pogresna tvrdnja zaista ne vrijedi.
Hint: protuprimjeri se obicno lako skuze iz onoga na cemu ti dokaz zapne.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |










