| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
 Postano: 15:31 uto, 12. 10. 2010 Naslov: Prostori, baze,... Postano: 15:31 uto, 12. 10. 2010 Naslov: Prostori, baze,... |
    |
|
|
Moze pomoc oko 2 zadatka?
1. Neka je n el. iz N i M={p e P(n); p(x)=p(-x), x e R}
Nadite jednu bazu nekog direktnog komplementa potprostora M u P(n) i odredite mu dimenziju.
2. Neka je V v.p, te neka su M i L njegovi potprostori. Pretpostavimo da je dim V=n<beskonacno, dim M= n-1 i L nije podskup od M. Dokazite:
a). ako je {a1,a2,...,an-1} baza za M i b el L\M, onda je {a1,a2,...an-1,b} baza za V.
b). V=L+M
Moze pomoc oko 2 zadatka?
1. Neka je n el. iz N i M={p e P(n); p(x)=p(-x), x e R}
Nadite jednu bazu nekog direktnog komplementa potprostora M u P(n) i odredite mu dimenziju.
2. Neka je V v.p, te neka su M i L njegovi potprostori. Pretpostavimo da je dim V=n<beskonacno, dim M= n-1 i L nije podskup od M. Dokazite:
a). ako je {a1,a2,...,an-1} baza za M i b el L\M, onda je {a1,a2,...an-1,b} baza za V.
b). V=L+M
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 16:36 uto, 12. 10. 2010 Naslov: Postano: 16:36 uto, 12. 10. 2010 Naslov: |
    |
|
|
1. Zadatak treba razbiti na dva slučaja: kad je n paran i kad nije. Ovdje ću razmotriti slučaj kad je n paran, a drugi ostavljam tebi. :)
Ako je n paran, kad raspišemo uvjet [latex]p(x) = p(-x)[/latex], dobimo [latex]a_n x^n + a_{n - 1} x^{n - 1} + \ldots + a_1 x + a_0 = a_n x^n - a_{n - 1} x^{n - 1} + \ldots - a_1 x + a_0[/latex], tj. [latex]a_{n - 1} x^{n - 1} + a_{n - 3} x^{n - 3} + \ldots + a_3 x^3 + a_1 x = 0[/latex]. (Možemo primjetiti da se pojavljuju samo neparni indeksi.) No, kako taj uvjet mora vrijediti za sve [latex]x \in \mathbb{R}[/latex], po jednakosti polinoma slijedi [latex]a_k = 0[/latex], za sve neparne k. Iz toga vidimo da je neki polinom iz M akko ima netrivijalne koeficijente samo uz parne potencije od x. Slijedi da je [latex]\{ 1, x^2, \ldots, x^{n - 2}, x^n \}[/latex] jedna baza. Lako vidimo da je onda [latex]\{ x, x^3, \ldots, x^{n - 3}, x^{n - 1} \}[/latex] jedna baza za neki direktni komplement od M i da mu je dimenzija n/2 (to lako uočimo ako primjetimo da eksponenti u toj bazi čine aritmetički niz s opčim članom [latex]2 k - 1[/latex], gdje k ide od 1 do n/2).
2. a) Trebamo dokazati da je neki skup baza, što znači da trebamo pokazati da je linearno nezavisan i da je skup izvodnica. Kako vidimo da taj skup ima dobar broj elemenata (dim V = n), dovoljno je pokazati, npr. linearnu nezavisnost.
Pogledajmo što znamo: skup [latex]\{ a_1, a_2, \ldots , a_{n - 1} \}[/latex] je baza, pa je time i linearno nezavisan, a mi želimo pokazati linearnu nezavisnost od [latex]\{ a_1, a_2, \ldots, a_{n - 1}, b \}[/latex], pa je dovoljno pokazati da se b ne može prikazati kao linearna kombinacija a-ova (to je istina zbog drugog dijela propozicije 2.2.4. iz [url=http://web.math.hr/nastava/la/razno/poglavlje2.pdf]skripte prof. Bakića[/url]).
Kad opet pogledamo na pretpostavke, vidimo [latex]b \in L \setminus M[/latex], što znači da [latex]b \notin M[/latex]. To odmah povlači da se b ne može prikazati kao linearna kombinacija a-ova, čime je ovaj dio zadatka dokazan.
b) Ovo možemo dokazati koristeći karakterizaciju sume potprostora ([latex]v \in L + M \ \Leftrightarrow \ (\exists \, x \in L)(\exists \, y \in M) \, v = x + y[/latex]). Inkluzija [latex]L + M \subseteq V[/latex] očito vrijedi.
Dokažimo obrnutu inkluziju. Neka je [latex]v \in V[/latex] proizvoljan. Iz dijela a) iskoristimo bazu, pa znamo da postoje skalari [latex]\alpha_1, \alpha_2, \ldots, \alpha_{n - 1}, \beta \in \mathbb{F}[/latex] takvi da je [latex]\displaystyle v = \sum_{i = 1}^{n - 1} \alpha_i a_i + \beta b[/latex]. Primjetimo da je [latex]\displaystyle x := \sum_{i = 1}^{n - 1} \alpha_i a_i \in M[/latex] i [latex]y := \beta b \in L[/latex]. Po spomenutoj karakterizaciji, slijedi da je [latex]v \in L + M[/latex].
Evo, ako nešto nije jasno, pitaj. :)
1. Zadatak treba razbiti na dva slučaja: kad je n paran i kad nije. Ovdje ću razmotriti slučaj kad je n paran, a drugi ostavljam tebi. 
Ako je n paran, kad raspišemo uvjet 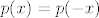 , dobimo , dobimo  , tj. , tj. 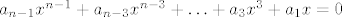 . (Možemo primjetiti da se pojavljuju samo neparni indeksi.) No, kako taj uvjet mora vrijediti za sve . (Možemo primjetiti da se pojavljuju samo neparni indeksi.) No, kako taj uvjet mora vrijediti za sve 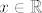 , po jednakosti polinoma slijedi , po jednakosti polinoma slijedi 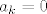 , za sve neparne k. Iz toga vidimo da je neki polinom iz M akko ima netrivijalne koeficijente samo uz parne potencije od x. Slijedi da je , za sve neparne k. Iz toga vidimo da je neki polinom iz M akko ima netrivijalne koeficijente samo uz parne potencije od x. Slijedi da je 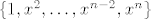 jedna baza. Lako vidimo da je onda jedna baza. Lako vidimo da je onda 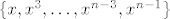 jedna baza za neki direktni komplement od M i da mu je dimenzija n/2 (to lako uočimo ako primjetimo da eksponenti u toj bazi čine aritmetički niz s opčim članom jedna baza za neki direktni komplement od M i da mu je dimenzija n/2 (to lako uočimo ako primjetimo da eksponenti u toj bazi čine aritmetički niz s opčim članom 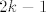 , gdje k ide od 1 do n/2). , gdje k ide od 1 do n/2).
2. a) Trebamo dokazati da je neki skup baza, što znači da trebamo pokazati da je linearno nezavisan i da je skup izvodnica. Kako vidimo da taj skup ima dobar broj elemenata (dim V = n), dovoljno je pokazati, npr. linearnu nezavisnost.
Pogledajmo što znamo: skup 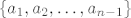 je baza, pa je time i linearno nezavisan, a mi želimo pokazati linearnu nezavisnost od je baza, pa je time i linearno nezavisan, a mi želimo pokazati linearnu nezavisnost od 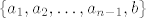 , pa je dovoljno pokazati da se b ne može prikazati kao linearna kombinacija a-ova (to je istina zbog drugog dijela propozicije 2.2.4. iz skripte prof. Bakića). , pa je dovoljno pokazati da se b ne može prikazati kao linearna kombinacija a-ova (to je istina zbog drugog dijela propozicije 2.2.4. iz skripte prof. Bakića).
Kad opet pogledamo na pretpostavke, vidimo 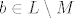 , što znači da , što znači da 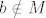 . To odmah povlači da se b ne može prikazati kao linearna kombinacija a-ova, čime je ovaj dio zadatka dokazan. . To odmah povlači da se b ne može prikazati kao linearna kombinacija a-ova, čime je ovaj dio zadatka dokazan.
b) Ovo možemo dokazati koristeći karakterizaciju sume potprostora (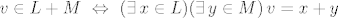 ). Inkluzija ). Inkluzija 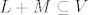 očito vrijedi. očito vrijedi.
Dokažimo obrnutu inkluziju. Neka je 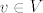 proizvoljan. Iz dijela a) iskoristimo bazu, pa znamo da postoje skalari proizvoljan. Iz dijela a) iskoristimo bazu, pa znamo da postoje skalari 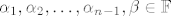 takvi da je takvi da je 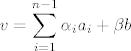 . Primjetimo da je . Primjetimo da je 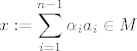 i i 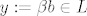 . Po spomenutoj karakterizaciji, slijedi da je . Po spomenutoj karakterizaciji, slijedi da je 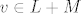 . .
Evo, ako nešto nije jasno, pitaj. 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 20:29 uto, 12. 10. 2010 Naslov: Postano: 20:29 uto, 12. 10. 2010 Naslov: |
    |
|
|
a) Neka je [latex](x_1,x_2,x_3) \in S[/latex] i [latex]\alpha \in \mathbb{C}[/latex]. Sada imamo:
[latex] \alpha (x_1,x_2,x_3) = (\alpha x_1,\alpha x_2,\alpha x_3)[/latex]
Uvrstimo dobivenu trojku u uvjet da se kompleksna trojka nalazi u S. Imamo:
[latex](\alpha ^{2} x_1^2 - \alpha^2 x_2 ^2)\alpha^2 x_3^2 \in \mathbb{R}
\Leftrightarrow \alpha^4 (x_1^2 - x_2 ^2)x_3^2 \in \mathbb{R}[/latex]
Buduci da je [latex](x_1^2 - x_2 ^2)x_3^2 \in \mathbb{R}[/latex] dovoljno je odabrati [latex] \alpha[/latex] takav da [latex]\alpha^4[/latex] nije realan i [latex](x_1^2 - x_2 ^2)x_3^2 \neq 0[/latex]pa tvrdnja opcenito ne vrijedi. Dakle [latex]S[/latex] nije potprostor od [latex]\mathbb{C}^3[/latex].
b) Neka su [latex]a_1 = (x_1, y_1, z_1), a_2 = (x_2, y_2, z_2) \in T[/latex]. Promatramo vektor [latex]\alpha(x_1, y_1, z_1)+\beta(x_2, y_2, z_2) = (\alpha x_1 + \beta x_2, \alpha y_1 + \beta y_2, \alpha z_1 + \beta z_2)[/latex]; trebamo pokazati da vrijedi [latex](\alpha x_1 + \beta x_2) - (\alpha y_1 + \beta y_2) + (\alpha z_1 + \beta z_2) = 0
[/latex]
Zaista, nakon sredivanja izraza dobivamo:
[latex]\alpha(x_1 - y_1 + z_1) + \beta(x_2 - y_2 + z_2) = 0[/latex]
sto je istina jer su [latex]a_1, a_2 \in T[/latex].
EDIT: zaboravio sam odrediti bazu i dimenziju u slucaju b), ali vec je pmli napravio pa necu dodavati :)
a) Neka je 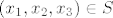 i i 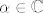 . Sada imamo: . Sada imamo:
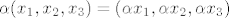
Uvrstimo dobivenu trojku u uvjet da se kompleksna trojka nalazi u S. Imamo:
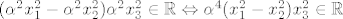
Buduci da je 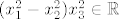 dovoljno je odabrati dovoljno je odabrati  takav da takav da 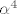 nije realan i nije realan i 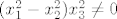 pa tvrdnja opcenito ne vrijedi. Dakle pa tvrdnja opcenito ne vrijedi. Dakle  nije potprostor od nije potprostor od 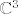 . .
b) Neka su 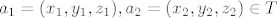 . Promatramo vektor . Promatramo vektor 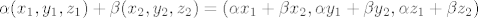 ; trebamo pokazati da vrijedi ; trebamo pokazati da vrijedi 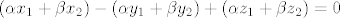
Zaista, nakon sredivanja izraza dobivamo:
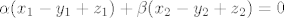
sto je istina jer su 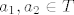 . .
EDIT: zaboravio sam odrediti bazu i dimenziju u slucaju b), ali vec je pmli napravio pa necu dodavati 
Zadnja promjena: Flame; 20:39 uto, 12. 10. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:29 uto, 12. 10. 2010 Naslov: Postano: 20:29 uto, 12. 10. 2010 Naslov: |
    |
|
|
[quote="CROmpir"]a) Je li skup S = {(x1; x2; x3) ∈ C3 : (x1^2-x2^2)x3^2 el. iz R} potprostor kompleksnog vektorskog prostora C3? Ako jest, odredite mu dimenziju i neku bazu.[/quote]
Nije, jer npr. [latex](2, 1, 1) \in S[/latex], ali [latex](2 + i) \cdot (2, 1, 1) = (4 + 2i, 2 + i, 2 + i) \notin S[/latex].
[quote="CROmpir"]b) Je li skup T = {(x; y; z) ∈ C3 : x − y + z = 0} potprostor kompleksnog vektorskog prostora C3? Ako jest, odredite mu dimenziju i neku bazu.[/quote]
Ovo jest. Izrazimo, npr. y, iz uvjeta da dobimo y = x + z, pa je [latex]T = \{ (x, x + z, z) : x, y \in \mathbb{C} \}[/latex]. Vidimo da je [latex](x, x + z, z) = x (1, 1, 0) + z (0, 1, 1)[/latex], što znači da je [latex]\{ (1, 1, 0), (0, 1, 1) \}[/latex] skup izvodnica za T. Lako se pokaže da je to i linearno nezavisan skup, pa je to onda jedna baza za T. Sad je očito dim T = 2.
[quote="CROmpir"]I ako moze neki hint na pitanje sto moraju vektori zadovoljavati da se nalaze u linearnoj ljusci skupa?[/quote]
Moraju se moći prikazati kao linearna kombinacija vektora iz tog skupa.
EDIT: Sad sam skužio da sam u b) dijelu zaboravio zaprav dokazati da je T doista potprostor (kao što je to učinio kolega Flame ;)). No, kad razmislim, dokazao sam da je [latex]T = [ \{ (1, 1, 0), (0, 1, 1) \} ][/latex], što povlači da je T vektorski prostor. Ipak preporučam da stvari dokazujete kako su vas vaši dragi asistenti naučili. :D
| CROmpir (napisa): | | a) Je li skup S = {(x1; x2; x3) ∈ C3 : (x1^2-x2^2)x3^2 el. iz R} potprostor kompleksnog vektorskog prostora C3? Ako jest, odredite mu dimenziju i neku bazu. |
Nije, jer npr. 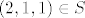 , ali , ali 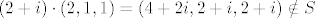 . .
| CROmpir (napisa): | | b) Je li skup T = {(x; y; z) ∈ C3 : x − y + z = 0} potprostor kompleksnog vektorskog prostora C3? Ako jest, odredite mu dimenziju i neku bazu. |
Ovo jest. Izrazimo, npr. y, iz uvjeta da dobimo y = x + z, pa je 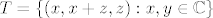 . Vidimo da je . Vidimo da je 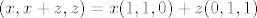 , što znači da je , što znači da je 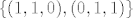 skup izvodnica za T. Lako se pokaže da je to i linearno nezavisan skup, pa je to onda jedna baza za T. Sad je očito dim T = 2. skup izvodnica za T. Lako se pokaže da je to i linearno nezavisan skup, pa je to onda jedna baza za T. Sad je očito dim T = 2.
| CROmpir (napisa): | | I ako moze neki hint na pitanje sto moraju vektori zadovoljavati da se nalaze u linearnoj ljusci skupa? |
Moraju se moći prikazati kao linearna kombinacija vektora iz tog skupa.
EDIT: Sad sam skužio da sam u b) dijelu zaboravio zaprav dokazati da je T doista potprostor (kao što je to učinio kolega Flame  ). No, kad razmislim, dokazao sam da je ). No, kad razmislim, dokazao sam da je 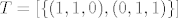 , što povlači da je T vektorski prostor. Ipak preporučam da stvari dokazujete kako su vas vaši dragi asistenti naučili. , što povlači da je T vektorski prostor. Ipak preporučam da stvari dokazujete kako su vas vaši dragi asistenti naučili. 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 10:02 sub, 30. 10. 2010 Naslov: Postano: 10:02 sub, 30. 10. 2010 Naslov: |
    |
|
|
Ako je n paran, kad raspišemo uvjet [latex]p(x) = p(-x)[/latex], dobimo [latex]a_n x^n + a_{n - 1} x^{n - 1} + \ldots + a_1 x + a_0 = a_n x^n - a_{n - 1} x^{n - 1} + \ldots - a_1 x + a_0[/latex], tj. [latex]a_{n - 1} x^{n - 1} + a_{n - 3} x^{n - 3} + \ldots + a_3 x^3 + a_1 x = 0[/latex]. (Možemo primjetiti da se pojavljuju samo neparni indeksi.) No, kako taj uvjet mora vrijediti za sve [latex]x \in \mathbb{R}[/latex], po jednakosti polinoma slijedi [latex]a_k = 0[/latex], za sve neparne k. Iz toga vidimo da je neki polinom iz M akko ima netrivijalne koeficijente samo uz parne potencije od x. Slijedi da je [latex]\{ 1, x^2, \ldots, x^{n - 2}, x^n \}[/latex] jedna baza. Lako vidimo da je onda [latex]\{ x, x^3, \ldots, x^{n - 3}, x^{n - 1} \}[/latex] jedna baza za neki direktni komplement od M i da mu je dimenzija n/2 (to lako uočimo ako primjetimo da eksponenti u toj bazi čine aritmetički niz s opčim članom [latex]2 k - 1[/latex], gdje k ide od 1 do n/2).
meni ispada i za neparan n isto kao za paran...nzm gdje griješim..ili je to moguće? =S
Ako je n paran, kad raspišemo uvjet 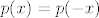 , dobimo , dobimo  , tj. , tj. 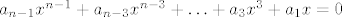 . (Možemo primjetiti da se pojavljuju samo neparni indeksi.) No, kako taj uvjet mora vrijediti za sve . (Možemo primjetiti da se pojavljuju samo neparni indeksi.) No, kako taj uvjet mora vrijediti za sve 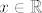 , po jednakosti polinoma slijedi , po jednakosti polinoma slijedi 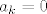 , za sve neparne k. Iz toga vidimo da je neki polinom iz M akko ima netrivijalne koeficijente samo uz parne potencije od x. Slijedi da je , za sve neparne k. Iz toga vidimo da je neki polinom iz M akko ima netrivijalne koeficijente samo uz parne potencije od x. Slijedi da je 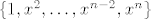 jedna baza. Lako vidimo da je onda jedna baza. Lako vidimo da je onda 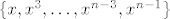 jedna baza za neki direktni komplement od M i da mu je dimenzija n/2 (to lako uočimo ako primjetimo da eksponenti u toj bazi čine aritmetički niz s opčim članom jedna baza za neki direktni komplement od M i da mu je dimenzija n/2 (to lako uočimo ako primjetimo da eksponenti u toj bazi čine aritmetički niz s opčim članom 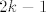 , gdje k ide od 1 do n/2). , gdje k ide od 1 do n/2).
meni ispada i za neparan n isto kao za paran...nzm gdje griješim..ili je to moguće? =S
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:06 sub, 30. 10. 2010 Naslov: Postano: 12:06 sub, 30. 10. 2010 Naslov: |
    |
|
|
Uzmimo da je [latex]n = 2 m - 1[/latex], za neki [latex]m \in \mathbb{N}[/latex]. Baza za M ispadne [latex]\{ 1, x^2, \ldots, x^{2 m - 4}, x^{2 m - 2}\}[/latex] (parni eksponenti). Jedna baza za neki komplement je [latex]\{ x, x^3, \ldots, x^{2 m - 3}, x^{2 m - 1} \}[/latex]. Dimenzija komplementa je [latex]m[/latex] (eksponenti su [latex]2 \cdot 1 - 1, 2 \cdot 2 - 1, \ldots, 2 (m - 1) - 1, 2 m - 1[/latex]), tj. [latex]\frac{n + 1}{2}[/latex].
Uzmimo da je 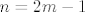 , za neki , za neki 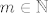 . Baza za M ispadne . Baza za M ispadne 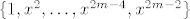 (parni eksponenti). Jedna baza za neki komplement je (parni eksponenti). Jedna baza za neki komplement je 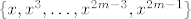 . Dimenzija komplementa je . Dimenzija komplementa je  (eksponenti su (eksponenti su 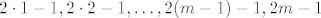 ), tj. ), tj. 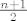 . .
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:52 sub, 30. 10. 2010 Naslov: Postano: 19:52 sub, 30. 10. 2010 Naslov: |
    |
|
|
[quote="Joker"]može li netko riješiti 3. pod b)[/quote]
Skup B nije vektorski prostor jer ne sadrži nulvektor.
To je važno dobro razumijeti. Ako je neki skup vektorski prostor, onda sadržava nulvektor (drugo po redu od osam svojstava v.p.). (Obrat po kontrapoziciji je: ako skup ne sadržava nulvektor, onda nije vektorski prostor.) Obrat NE vrijedi, tj. ako vidiš da neki skup ima nulvektor, on ne mora biti vektorski prostor.
[quote="Joker"]i 4. zadatak,zadnja dva pitanja...drugo pitanje ne razumijem a trece,pretpostavljam da 4 vektora nikada nece biti linearno nezavisna u v3(o)...???[/quote]
Drugo pitanje znači da trebaš odrediti za koje [latex]\lambda \in \mathbb{R}[/latex] vrijedi [latex]\alpha \vec{a} + \beta \vec{b} + \gamma \vec{c} = \vec{d}[/latex], za neke [latex]\alpha, \beta, \gamma \in \mathbb{R}[/latex].
U pravu si što se tiče trećeg pitanja. Dokazali ste na predavanjima da je broj elemenata linearno nezavisnog skupa manji ili jednak od dimenzije v.p. u kojem se nalazi.
| Joker (napisa): | | može li netko riješiti 3. pod b) |
Skup B nije vektorski prostor jer ne sadrži nulvektor.
To je važno dobro razumijeti. Ako je neki skup vektorski prostor, onda sadržava nulvektor (drugo po redu od osam svojstava v.p.). (Obrat po kontrapoziciji je: ako skup ne sadržava nulvektor, onda nije vektorski prostor.) Obrat NE vrijedi, tj. ako vidiš da neki skup ima nulvektor, on ne mora biti vektorski prostor.
| Joker (napisa): | | i 4. zadatak,zadnja dva pitanja...drugo pitanje ne razumijem a trece,pretpostavljam da 4 vektora nikada nece biti linearno nezavisna u v3(o)...??? |
Drugo pitanje znači da trebaš odrediti za koje 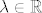 vrijedi vrijedi 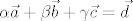 , za neke , za neke 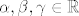 . .
U pravu si što se tiče trećeg pitanja. Dokazali ste na predavanjima da je broj elemenata linearno nezavisnog skupa manji ili jednak od dimenzije v.p. u kojem se nalazi.
|
|
| [Vrh] |
|
mayam
Forumaš(ica)

Pridružen/a: 20. 10. 2010. (18:31:42)
Postovi: (C)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
mayam
Forumaš(ica)

Pridružen/a: 20. 10. 2010. (18:31:42)
Postovi: (C)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 20:19 čet, 4. 11. 2010 Naslov: Postano: 20:19 čet, 4. 11. 2010 Naslov: |
    |
|
|
M= { (x1, x2, x3, x4) € R^4 } x1- x2+x3+x4=0, x1-2*x2-x4=0}
Dokazala sam da je potprostor R^4, ali ne znam bazu odredit, odnosno skup izvodnice.
rekli smo da uvjete rjesavamo kao sustave jednadzbi, pa sam dobila
x= ( t, r, -2t+3r, t-2r)
Kako sad da na osnovu toga odredim bazu?
Na vjezbama smo imali lagano, bilo je
x= (t, t, s, t) uz uvjete x1-x2=0 i x1+x2-2x4=0, te se je lako odredila baza....
t (1,1,0,1) + s ( 0,0,1,0)= (zagrade su iz M) nezavisni su, sto znaci baza je.
A kako sad u mom slucaju.
Pliz help!! hvala
M= { (x1, x2, x3, x4) € R^4 } x1- x2+x3+x4=0, x1-2*x2-x4=0}
Dokazala sam da je potprostor R^4, ali ne znam bazu odredit, odnosno skup izvodnice.
rekli smo da uvjete rjesavamo kao sustave jednadzbi, pa sam dobila
x= ( t, r, -2t+3r, t-2r)
Kako sad da na osnovu toga odredim bazu?
Na vjezbama smo imali lagano, bilo je
x= (t, t, s, t) uz uvjete x1-x2=0 i x1+x2-2x4=0, te se je lako odredila baza....
t (1,1,0,1) + s ( 0,0,1,0)= (zagrade su iz M) nezavisni su, sto znaci baza je.
A kako sad u mom slucaju.
Pliz help!! hvala
|
|
| [Vrh] |
|
Linadus
Forumaš(ica)
Pridružen/a: 07. 09. 2010. (12:57:28)
Postovi: (2C)16
|
 Postano: 20:33 čet, 4. 11. 2010 Naslov: Postano: 20:33 čet, 4. 11. 2010 Naslov: |
    |
|
|
[quote="frutabella"]M= { (x1, x2, x3, x4) € R^4 } x1- x2+x3+x4=0, x1-2*x2-x4=0}
Dokazala sam da je potprostor R^4, ali ne znam bazu odredit, odnosno skup izvodnice.
rekli smo da uvjete rjesavamo kao sustave jednadzbi, pa sam dobila
x= ( t, r, -2t+3r, t-2r)
Kako sad da na osnovu toga odredim bazu?
Na vjezbama smo imali lagano, bilo je
x= (t, t, s, t) uz uvjete x1-x2=0 i x1+x2-2x4=0, te se je lako odredila baza....
t (1,1,0,1) + s ( 0,0,1,0)= (zagrade su iz M) nezavisni su, sto znaci baza je.
A kako sad u mom slucaju.
Pliz help!! hvala[/quote]
pa nije ništa teže...x= ( t, r, -2t+3r, t-2r) = (t, 0, -2t, t) + (0, r, 3r, -2r) = t(1,0,-2,1)+r(0,1,3,-2); dalje isto
iako mislim da si negdje fulala racun jer je meni ispalo (1,0,-2,1) i (2,1,-1,0)...
| frutabella (napisa): | M= { (x1, x2, x3, x4) € R^4 } x1- x2+x3+x4=0, x1-2*x2-x4=0}
Dokazala sam da je potprostor R^4, ali ne znam bazu odredit, odnosno skup izvodnice.
rekli smo da uvjete rjesavamo kao sustave jednadzbi, pa sam dobila
x= ( t, r, -2t+3r, t-2r)
Kako sad da na osnovu toga odredim bazu?
Na vjezbama smo imali lagano, bilo je
x= (t, t, s, t) uz uvjete x1-x2=0 i x1+x2-2x4=0, te se je lako odredila baza....
t (1,1,0,1) + s ( 0,0,1,0)= (zagrade su iz M) nezavisni su, sto znaci baza je.
A kako sad u mom slucaju.
Pliz help!! hvala |
pa nije ništa teže...x= ( t, r, -2t+3r, t-2r) = (t, 0, -2t, t) + (0, r, 3r, -2r) = t(1,0,-2,1)+r(0,1,3,-2); dalje isto
iako mislim da si negdje fulala racun jer je meni ispalo (1,0,-2,1) i (2,1,-1,0)...
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 21:21 čet, 4. 11. 2010 Naslov: Postano: 21:21 čet, 4. 11. 2010 Naslov: |
    |
|
|
[quote="Linadus"][quote="frutabella"]M= { (x1, x2, x3, x4) € R^4 } x1- x2+x3+x4=0, x1-2*x2-x4=0}
Dokazala sam da je potprostor R^4, ali ne znam bazu odredit, odnosno skup izvodnice.
rekli smo da uvjete rjesavamo kao sustave jednadzbi, pa sam dobila
x= ( t, r, -2t+3r, t-2r)
Kako sad da na osnovu toga odredim bazu?
Na vjezbama smo imali lagano, bilo je
x= (t, t, s, t) uz uvjete x1-x2=0 i x1+x2-2x4=0, te se je lako odredila baza....
t (1,1,0,1) + s ( 0,0,1,0)= (zagrade su iz M) nezavisni su, sto znaci baza je.
A kako sad u mom slucaju.
Pliz help!! hvala[/quote]
pa nije ništa teže...x= ( t, r, -2t+3r, t-2r) = (t, 0, -2t, t) + (0, r, 3r, -2r) = t(1,0,-2,1)+r(0,1,3,-2); dalje isto
iako mislim da si negdje fulala racun jer je meni ispalo (1,0,-2,1) i (2,1,-1,0)...[/quote]
ne znas gdje sam mogla fulati? gledam a ne znam gdje sam mogla, hm...
HVALA TI PUNO! Nisam znala na koji nacin je asis. to uradila, znaci uzmes jednom da je t=0 i r=0, to dvoje zbrojis... i onda stavi t=r=1. i dobijes baze.
[size=9][color=#999999]Added after 31 minutes:[/color][/size]
Ujh, sad mi ovo nesto steka....ako je netko voljan da pomogne...
odrediti bazu za ovo:
p€M
znaci opci oblik polinoma je: p(t)= ao + a1t + a2t^2
imam sljedece uvjete : p'(0) + p (1)=0 i p(0)+p'(1)=0
znaci: p'(t)= a1 + 2*a2t
slijedi: 1) p'(0)+p(1)= a1 + ao + a1 + a2 = ao + 2a1 + a2 = 0 -----> odavde
valjda slijedi da je: a0= -2a1 - 2a2 (sto uvrstimo dole u jednadzbu)
2) p(0) + p' (1) = ao + a1 + 2*a2 = 0 (kad uvrstimo tu ono gore,
dobivamo da je a1=0 ).
Ja sam to a1= 0 opet uvrstila gore i dobila da je ao = -2a2
Sto znaci da je p(t) = -2a2 + a2t^2.
KAKO SAD ODREDITI NA OSNOVU TOGA STO JE SKUP IZVODNICA?
| Linadus (napisa): | | frutabella (napisa): | M= { (x1, x2, x3, x4) € R^4 } x1- x2+x3+x4=0, x1-2*x2-x4=0}
Dokazala sam da je potprostor R^4, ali ne znam bazu odredit, odnosno skup izvodnice.
rekli smo da uvjete rjesavamo kao sustave jednadzbi, pa sam dobila
x= ( t, r, -2t+3r, t-2r)
Kako sad da na osnovu toga odredim bazu?
Na vjezbama smo imali lagano, bilo je
x= (t, t, s, t) uz uvjete x1-x2=0 i x1+x2-2x4=0, te se je lako odredila baza....
t (1,1,0,1) + s ( 0,0,1,0)= (zagrade su iz M) nezavisni su, sto znaci baza je.
A kako sad u mom slucaju.
Pliz help!! hvala |
pa nije ništa teže...x= ( t, r, -2t+3r, t-2r) = (t, 0, -2t, t) + (0, r, 3r, -2r) = t(1,0,-2,1)+r(0,1,3,-2); dalje isto
iako mislim da si negdje fulala racun jer je meni ispalo (1,0,-2,1) i (2,1,-1,0)... |
ne znas gdje sam mogla fulati? gledam a ne znam gdje sam mogla, hm...
HVALA TI PUNO! Nisam znala na koji nacin je asis. to uradila, znaci uzmes jednom da je t=0 i r=0, to dvoje zbrojis... i onda stavi t=r=1. i dobijes baze.
Added after 31 minutes:
Ujh, sad mi ovo nesto steka....ako je netko voljan da pomogne...
odrediti bazu za ovo:
p€M
znaci opci oblik polinoma je: p(t)= ao + a1t + a2t^2
imam sljedece uvjete : p'(0) + p (1)=0 i p(0)+p'(1)=0
znaci: p'(t)= a1 + 2*a2t
slijedi: 1) p'(0)+p(1)= a1 + ao + a1 + a2 = ao + 2a1 + a2 = 0 -----> odavde
valjda slijedi da je: a0= -2a1 - 2a2 (sto uvrstimo dole u jednadzbu)
2) p(0) + p' (1) = ao + a1 + 2*a2 = 0 (kad uvrstimo tu ono gore,
dobivamo da je a1=0 ).
Ja sam to a1= 0 opet uvrstila gore i dobila da je ao = -2a2
Sto znaci da je p(t) = -2a2 + a2t^2.
KAKO SAD ODREDITI NA OSNOVU TOGA STO JE SKUP IZVODNICA?
|
|
| [Vrh] |
|
Bruno
Gost
|
 Postano: 2:36 pet, 5. 11. 2010 Naslov: Postano: 2:36 pet, 5. 11. 2010 Naslov: |
    |
|
|
Imas sustav a0 + 2*a1 + a2 = 0, a0 + a1 + 2*a2 = 0 iz cega slijedi
a1, a2=a1, a0=-3*a1. Dakle polinom ti je oblika P(t) = -3*a1 + a1*t + a1*t^2 = a1(-3 + t + t^2) pa je a1 neki slobodni parametar (proizvoljan), a ovo u zagradama baza.
Sorry ako sam nesto (ili sve fulao), my vision's blurred jer je kasno. :s
Imas sustav a0 + 2*a1 + a2 = 0, a0 + a1 + 2*a2 = 0 iz cega slijedi
a1, a2=a1, a0=-3*a1. Dakle polinom ti je oblika P(t) = -3*a1 + a1*t + a1*t^2 = a1(-3 + t + t^2) pa je a1 neki slobodni parametar (proizvoljan), a ovo u zagradama baza.
Sorry ako sam nesto (ili sve fulao), my vision's blurred jer je kasno. :s
|
|
| [Vrh] |
|
|











