| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 19:41 pon, 18. 10. 2010 Naslov: 4. zadatak iz zadaće Postano: 19:41 pon, 18. 10. 2010 Naslov: 4. zadatak iz zadaće |
    |
|
|
http://web.math.hr/nastava/la/la_1_1011_dz1.pdf
Jasno mi je zašto vrijedi ta ekvivalencija, ali kao i obično imam problema sa formalnim dokazivanjem.
Dakle, ako je [latex]\alpha_n = 0[/latex], onda je [latex]a = \sum_{i=1}^{n-1} \alpha_i b_i[/latex] linearna kombinacija od [latex]\{b_1,b_2,...,b_{n-1} \}[/latex] i tako [latex]\{b_1,b_2,...,b_{n-1}, a \} [/latex]ne može biti baza.
No imam osjećaj da to nije dovoljno za ovaj zadatak. Ili jest?
http://web.math.hr/nastava/la/la_1_1011_dz1.pdf
Jasno mi je zašto vrijedi ta ekvivalencija, ali kao i obično imam problema sa formalnim dokazivanjem.
Dakle, ako je 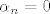 , onda je , onda je 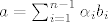 linearna kombinacija od linearna kombinacija od 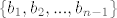 i tako i tako 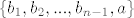 ne može biti baza. ne može biti baza.
No imam osjećaj da to nije dovoljno za ovaj zadatak. Ili jest?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 19:54 pon, 18. 10. 2010 Naslov: Postano: 19:54 pon, 18. 10. 2010 Naslov: |
    |
|
|
U zadatku se trazi da dokazes ekvivalenciju (ako i samo ako).
Tu si dobro primjetio (la?) da [latex]\alpha _n=0[/latex] povlaci zavisnost onog skupa, koji zato ne moze biti baza. Ali to je, popularno receno, tek pola zadatka (smjer => ). Trebalo bi jos dokazati:
ako je skup [latex]\alpha _n \neq 0[/latex], onda je [latex]\{ b_1,\dots,b_{n-1},a\} [/latex] doista baza
U zadatku se trazi da dokazes ekvivalenciju (ako i samo ako).
Tu si dobro primjetio (la?) da  povlaci zavisnost onog skupa, koji zato ne moze biti baza. Ali to je, popularno receno, tek pola zadatka (smjer ⇒ ). Trebalo bi jos dokazati: povlaci zavisnost onog skupa, koji zato ne moze biti baza. Ali to je, popularno receno, tek pola zadatka (smjer ⇒ ). Trebalo bi jos dokazati:
ako je skup  , onda je , onda je 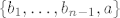 doista baza doista baza
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 20:52 pon, 18. 10. 2010 Naslov: Postano: 20:52 pon, 18. 10. 2010 Naslov: |
    |
|
|
Ako je skup [latex]\alpha _n \neq 0[/latex] , onda je [latex]\{ b_1,\dots,b_{n-1},a\} [/latex] baza:
OK, da bi taj skup bio baza on mora biti linearno nezavisan i sistem izvodnica.
Linearna nezavisnost:
Znamo otprije da su vektori [latex]\{ b_1,\dots,b_{n-1}\} [/latex] međusobno nezavisni (jer se nalaze u bazi vektorskog prostora V).
Treba samo dokazati da se a ne može prikazati kao linearna kombinacija od [latex]\{ b_1,\dots,b_{n-1}\} [/latex].
Pretpostavimo suprotno, tj. da se može prikazati tako:
''a'' ću zapisati kao [latex]a = \sum_{i=1}^{n-1} \alpha_i b_i + \alpha_nb_n[/latex] , pa onda imamo:
[latex] \sum_{i=1}^{n-1} \alpha_i b_i = \sum_{i=1}^{n-1} \alpha_i b_i + \alpha_nb_n[/latex]
[latex]0 = \alpha_nb_n[/latex]
Tu dolazimo do kontradikcije, jer u uvjetu imamo da [latex]
\alpha _n \neq 0[/latex], a kako je [latex] b_n [/latex] element baze vektorskog prostora V - on isto ne smije biti nula.
Znači, dokazali smo da je taj skup linearno nezavisan.
A sad, za dokazati da je skup sistem izvodnica, otprilike mi je jasno kako bi se to trebalo izvesti, prikazati neki proizvoljni vektor v kao linearnu kombinaciju prve baze (b1...bn) pa tako doći do toga da se taj vektor također može pokazati kao linearna kombinacija ove druge baze... ali tu sam se malo spetljao. Može kakav hint?
I naravno, da li ovo za l.n. valja?
Ako je skup  , onda je , onda je 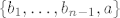 baza: baza:
OK, da bi taj skup bio baza on mora biti linearno nezavisan i sistem izvodnica.
Linearna nezavisnost:
Znamo otprije da su vektori 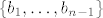 međusobno nezavisni (jer se nalaze u bazi vektorskog prostora V). međusobno nezavisni (jer se nalaze u bazi vektorskog prostora V).
Treba samo dokazati da se a ne može prikazati kao linearna kombinacija od 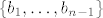 . .
Pretpostavimo suprotno, tj. da se može prikazati tako:
''a'' ću zapisati kao 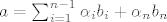 , pa onda imamo: , pa onda imamo:
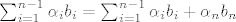
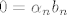
Tu dolazimo do kontradikcije, jer u uvjetu imamo da 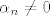 , a kako je , a kako je 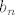 element baze vektorskog prostora V - on isto ne smije biti nula. element baze vektorskog prostora V - on isto ne smije biti nula.
Znači, dokazali smo da je taj skup linearno nezavisan.
A sad, za dokazati da je skup sistem izvodnica, otprilike mi je jasno kako bi se to trebalo izvesti, prikazati neki proizvoljni vektor v kao linearnu kombinaciju prve baze (b1...bn) pa tako doći do toga da se taj vektor također može pokazati kao linearna kombinacija ove druge baze... ali tu sam se malo spetljao. Može kakav hint?
I naravno, da li ovo za l.n. valja?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 22:07 pon, 18. 10. 2010 Naslov: Postano: 22:07 pon, 18. 10. 2010 Naslov: |
    |
|
|
Hm, da, previdio sam to.
A mogu li ići ovako:
[latex]\{ b_1,\dots,b_n\} [/latex] je sistem izvodnica.
[latex]\{ b_1,\dots,b_{n-1}, a\} [/latex] je također sistem izvodnica (pošto je svaki nadskup nekog sistema izvodnica također sistem izvodnica.)
[latex]b_n [/latex] se može prikazati kao linearna kombinacija ostalih elemenata, pa je onda i [latex]\{ b_1,\dots,b_{n-1}, a\} [/latex] sistem izvodnica, a također i baza zbog dobrog broja elemenata.
???
Hm, da, previdio sam to.
A mogu li ići ovako:
 je sistem izvodnica. je sistem izvodnica.
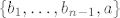 je također sistem izvodnica (pošto je svaki nadskup nekog sistema izvodnica također sistem izvodnica.) je također sistem izvodnica (pošto je svaki nadskup nekog sistema izvodnica također sistem izvodnica.)
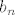 se može prikazati kao linearna kombinacija ostalih elemenata, pa je onda i se može prikazati kao linearna kombinacija ostalih elemenata, pa je onda i 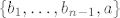 sistem izvodnica, a također i baza zbog dobrog broja elemenata. sistem izvodnica, a također i baza zbog dobrog broja elemenata.
???
Zadnja promjena: ceps; 22:22 pon, 18. 10. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 22:18 pon, 18. 10. 2010 Naslov: Postano: 22:18 pon, 18. 10. 2010 Naslov: |
    |
|
|
Al uoci da ovaj drugi skup nije nadskup prvog (ne sadrzi bn).
Preko nezavisnosti je ok:
Kad bi [latex]\{b_1,\dots,b_{n-1},a\}[/latex] bio zavisan skup, onda bi se a mogao prikazati kao kombinacija [latex]b_1,\dots, b_{n-1}[/latex] (zbog one jedne leme na predavanju; tu je jos bitno uociti da se niti jedan od b-ova ne moze prikazati pomocu prethodnika)
Ocito se a ne moze prikazati samo pomocu prvih n-1 b-ova jer je onaj alfa_n razlicit od nule =>kontradikcija, skup je nezavisan, pa je baza
Al uoci da ovaj drugi skup nije nadskup prvog (ne sadrzi bn).
Preko nezavisnosti je ok:
Kad bi 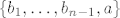 bio zavisan skup, onda bi se a mogao prikazati kao kombinacija bio zavisan skup, onda bi se a mogao prikazati kao kombinacija 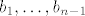 (zbog one jedne leme na predavanju; tu je jos bitno uociti da se niti jedan od b-ova ne moze prikazati pomocu prethodnika) (zbog one jedne leme na predavanju; tu je jos bitno uociti da se niti jedan od b-ova ne moze prikazati pomocu prethodnika)
Ocito se a ne moze prikazati samo pomocu prvih n-1 b-ova jer je onaj alfa_n razlicit od nule ⇒kontradikcija, skup je nezavisan, pa je baza
Zadnja promjena: pbakic; 22:23 pon, 18. 10. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 22:20 pon, 18. 10. 2010 Naslov: Postano: 22:20 pon, 18. 10. 2010 Naslov: |
    |
|
|
Argh, hvala puno. Malo sam valjda previše radio zadataka danas, a ''zadao'' sam si da ovaj moram dovršit danas, pa sam počeo radit glupaste greške...
Zapravo sam lapsus napravio:
[latex]\{ b_1,\dots,b_n\} [/latex] je sistem izvodnica.
[latex]\{ b_1,\dots,b_{n-1}, b_n, a\} [/latex] je također sistem izvodnica (pošto je svaki nadskup nekog sistema izvodnica također sistem izvodnica.)
[latex]b_n [/latex] se može prikazati kao linearna kombinacija ostalih elemenata, pa je onda i [latex]\{ b_1,\dots,b_{n-1}, a\} [/latex] sistem izvodnica, a također i baza zbog dobrog broja elemenata.
Samo iz znatiželje, da li može ovako?
Argh, hvala puno. Malo sam valjda previše radio zadataka danas, a ''zadao'' sam si da ovaj moram dovršit danas, pa sam počeo radit glupaste greške...
Zapravo sam lapsus napravio:
 je sistem izvodnica. je sistem izvodnica.
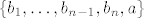 je također sistem izvodnica (pošto je svaki nadskup nekog sistema izvodnica također sistem izvodnica.) je također sistem izvodnica (pošto je svaki nadskup nekog sistema izvodnica također sistem izvodnica.)
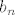 se može prikazati kao linearna kombinacija ostalih elemenata, pa je onda i se može prikazati kao linearna kombinacija ostalih elemenata, pa je onda i 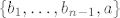 sistem izvodnica, a također i baza zbog dobrog broja elemenata. sistem izvodnica, a također i baza zbog dobrog broja elemenata.
Samo iz znatiželje, da li može ovako?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
mayam
Forumaš(ica)

Pridružen/a: 20. 10. 2010. (18:31:42)
Postovi: (C)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 19:01 sri, 20. 10. 2010 Naslov: Postano: 19:01 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="mayam"]a zasto se bn moze prikazati kao linearna kombinacija prethodnika kada je on u bazi???[/quote]
Mozda zato sto je baza ujedno i sustav izvodnica, a sustav izvod, znaci da se svaki vektor moze prikazati pomocu ostalih vektora iz sustava izvodnica. Hmm...valjda.
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="frutabella"][quote="mayam"]a zasto se bn moze prikazati kao linearna kombinacija prethodnika kada je on u bazi???[/quote]
Mozda zato sto je baza ujedno i sustav izvodnica, a sustav izvod, znaci da se svaki vektor moze prikazati pomocu ostalih vektora iz sustava izvodnica. Hmm...valjda.[/quote]
i zato smo bn izbacili i umjesto njega stavili a, kako nebi mijenjali broj elemenata, odnosno bazu.
Ako sam u krivu neka netko ispravi molim vas.
| mayam (napisa): | | a zasto se bn moze prikazati kao linearna kombinacija prethodnika kada je on u bazi??? |
Mozda zato sto je baza ujedno i sustav izvodnica, a sustav izvod, znaci da se svaki vektor moze prikazati pomocu ostalih vektora iz sustava izvodnica. Hmm...valjda.
Added after 1 minutes:
| frutabella (napisa): | | mayam (napisa): | | a zasto se bn moze prikazati kao linearna kombinacija prethodnika kada je on u bazi??? |
Mozda zato sto je baza ujedno i sustav izvodnica, a sustav izvod, znaci da se svaki vektor moze prikazati pomocu ostalih vektora iz sustava izvodnica. Hmm...valjda. |
i zato smo bn izbacili i umjesto njega stavili a, kako nebi mijenjali broj elemenata, odnosno bazu.
Ako sam u krivu neka netko ispravi molim vas.
|
|
| [Vrh] |
|
mayam
Forumaš(ica)

Pridružen/a: 20. 10. 2010. (18:31:42)
Postovi: (C)16
|
|
| [Vrh] |
|
travana
Forumaš(ica)

Pridružen/a: 22. 09. 2010. (17:12:41)
Postovi: (16)16
Spol: 
|
|
| [Vrh] |
|
mayam
Forumaš(ica)

Pridružen/a: 20. 10. 2010. (18:31:42)
Postovi: (C)16
|
|
| [Vrh] |
|
|









