| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
glmat
Forumaš(ica)

Pridružen/a: 19. 10. 2010. (22:17:53)
Postovi: (2)16
|
 Postano: 22:19 uto, 19. 10. 2010 Naslov: Odrediti parametar da bi skup vektora bio baza Postano: 22:19 uto, 19. 10. 2010 Naslov: Odrediti parametar da bi skup vektora bio baza |
    |
|
|
Pozdrav!
Jel mi može netko detaljno objasniti kako riješiti prvi zadatak iz zadaće?
Glasi ovako:
odredite [latex]t \in \mathbb{R}[/latex] za koje je skup {(1,1,0) , (1,-1,4) , (3,1,t)} baza vektorskog prostora R^3
znam da je lagano, al nikako se nemogu sjetit kako to tocno ide
Pozdrav!
Jel mi može netko detaljno objasniti kako riješiti prvi zadatak iz zadaće?
Glasi ovako:
odredite  za koje je skup {(1,1,0) , (1,-1,4) , (3,1,t)} baza vektorskog prostora R^3 za koje je skup {(1,1,0) , (1,-1,4) , (3,1,t)} baza vektorskog prostora R^3
znam da je lagano, al nikako se nemogu sjetit kako to tocno ide
|
|
| [Vrh] |
|
n.n.
Gost
|
|
| [Vrh] |
|
mhaberl
Forumaš(ica)

Pridružen/a: 05. 09. 2009. (14:44:26)
Postovi: (2D)16
Spol: 
Sarma: -
|
 Postano: 1:47 sri, 20. 10. 2010 Naslov: Re: Odrediti parametar da bi skup vektora bio baza Postano: 1:47 sri, 20. 10. 2010 Naslov: Re: Odrediti parametar da bi skup vektora bio baza |
    |
|
|
[quote="glmat"]Pozdrav!
Jel mi može netko detaljno objasniti kako riješiti prvi zadatak iz zadaće?
Glasi ovako:
odredite [latex]t \in \mathbb{R}[/latex] za koje je skup {(1,1,0) , (1,-1,4) , (3,1,t)} baza vektorskog prostora R^3
znam da je lagano, al nikako se nemogu sjetit kako to tocno ide[/quote]
Taj skup ce biti baza ako vrijedi:
[latex]\alpha \cdot (1,1,0) + \beta \cdot (1,-1,4) + \gamma \cdot (3,1,t) = (0,0,0) \iff \alpha = \beta = \gamma = 0[/latex]
odnosno [u][b]nece[/b][/u] biti baza ako postoje [latex] \alpha , \beta , \gamma \in \mathbb{R} [/latex] takvi da je bar jedan od njih [latex] \neq 0[/latex] i vrijedi [latex] \alpha \cdot (1,1,0) + \beta \cdot (1,-1,4) + \gamma \cdot (3,1,t) = (0,0,0)[/latex]
Pretpostavimo sad da taj skup nije baza, tada [bg=cyan]ocito[/bg] [latex]\gamma \neq 0[/latex]
_____
[bg=cyan]Zasto?[/bg]
Jer bi u suprotnom trebalo biti [latex]\alpha \neq 0[/latex] ili [latex]\beta \neq 0[/latex]
onda imas slucajeve
1) [latex]\alpha \neq 0[/latex] ili [latex]\beta = 0[/latex]
pa onda [latex]\alpha \cdot (1,1,0) = (0,0,0)[/latex] kontradikcija
2) [latex]\alpha = 0[/latex] ili [latex]\beta \neq 0[/latex]
pa onda [latex]\beta \cdot (1,-1,4) = (0,0,0)[/latex] kontradikcija
3) [latex]\alpha \neq 0[/latex] ili [latex]\beta \neq 0[/latex]
[latex]\frac{- \alpha}{\beta} \cdot (1,1,0) =(1,-1,4)[/latex]
pa iz toga [latex]\frac{- \alpha}{\beta} \cdot 0 = 4 [/latex] kontradikcija
____
kako je sad [latex]\gamma \neq 0[/latex] podjelis sve s njim i dobijes:
[latex] \frac{- \alpha}{\gamma} \cdot (1,1,0) + \frac{- \beta}{\gamma} \cdot (1,-1,4) = (3,1,t) [/latex]
od tuda:
[b]1)[/b] [latex] \frac{- \alpha}{\gamma} + \frac{- \beta}{\gamma} = 3 [/latex]
[b]2)[/b] [latex] \frac{- \alpha}{\gamma} - \frac{- \beta}{\gamma} = 1 [/latex]
[b]3)[/b] [latex] \frac{- \beta}{\gamma} \cdot 4 = t [/latex]
pa iz [b]1)[/b] i [b]2)[/b] : [latex] \frac{- \alpha}{\gamma} = 2, \frac{- \beta}{\gamma} = 1 [/latex]
i onda: [latex]t= 4[/latex][color=red] *[/color]
znaci, [u][b]jedino[/b][/u] ako je [latex]t = 4[/latex] gornji sustav ima rjesenje, odnosno postoje takvi [latex] \alpha , \beta , \gamma \in \mathbb{R} [/latex] takvi da je bar jedan od njih [latex] \neq 0[/latex] ( npr. [latex](\alpha , \beta , \gamma)=(-2, -1, 1)[/latex] ) i vrijedi [latex] \alpha \cdot (1,1,0) + \beta \cdot (1,-1,4) + \gamma \cdot (3,1,t) = (0,0,0)[/latex], tj. taj skup nije baza
Tebe se u zadatku trazilo da odredis za koje [latex] t \in \mathbb{R} [/latex] sustav [b]jest[/b] baza, a odgovor je za [latex] t \in \mathbb{R} \backslash \{ 4 \} [/latex]
- ispravljeno, bila je greska kod [color=red]*[/color]
| glmat (napisa): | Pozdrav!
Jel mi može netko detaljno objasniti kako riješiti prvi zadatak iz zadaće?
Glasi ovako:
odredite  za koje je skup {(1,1,0) , (1,-1,4) , (3,1,t)} baza vektorskog prostora R^3 za koje je skup {(1,1,0) , (1,-1,4) , (3,1,t)} baza vektorskog prostora R^3
znam da je lagano, al nikako se nemogu sjetit kako to tocno ide |
Taj skup ce biti baza ako vrijedi:

odnosno nece biti baza ako postoje 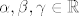 takvi da je bar jedan od njih takvi da je bar jedan od njih 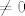 i vrijedi i vrijedi 
Pretpostavimo sad da taj skup nije baza, tada ocito 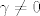
_____
Zasto?
Jer bi u suprotnom trebalo biti 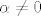 ili ili 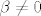
onda imas slucajeve
1) 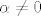 ili ili 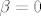
pa onda 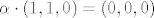 kontradikcija kontradikcija
2)  ili ili 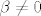
pa onda  kontradikcija kontradikcija
3) 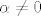 ili ili 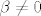
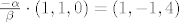
pa iz toga 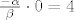 kontradikcija kontradikcija
____
kako je sad 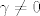 podjelis sve s njim i dobijes: podjelis sve s njim i dobijes:
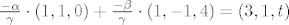
od tuda:
1) 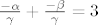
2) 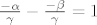
3) 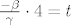
pa iz 1) i 2) : 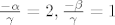
i onda:  * *
znaci, jedino ako je  gornji sustav ima rjesenje, odnosno postoje takvi gornji sustav ima rjesenje, odnosno postoje takvi 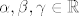 takvi da je bar jedan od njih takvi da je bar jedan od njih 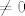 ( npr. ( npr. 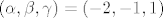 ) i vrijedi ) i vrijedi  , tj. taj skup nije baza , tj. taj skup nije baza
Tebe se u zadatku trazilo da odredis za koje  sustav jest baza, a odgovor je za sustav jest baza, a odgovor je za 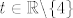
- ispravljeno, bila je greska kod *
Zadnja promjena: mhaberl; 11:32 sri, 20. 10. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
mhaberl
Forumaš(ica)

Pridružen/a: 05. 09. 2009. (14:44:26)
Postovi: (2D)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
n.n.
Gost
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 12:37 sri, 20. 10. 2010 Naslov: Postano: 12:37 sri, 20. 10. 2010 Naslov: |
    |
|
|
Ja ovako razmisljam...Posto smo u trodimenzionalnom prostoru (sto zakljucujemo iz R^3= dim3) znamo da baza mora imati 3 člana (kao sto ima, u zadatku je vec zadana tročlana baza- jer da nije troclana, da ima vise clanova trebali bi reducirati do baze, izbacivati clanove koji su zavisni i tako doci do nezavisnog skupa).
Znaci, posto vec imamo tri clana, potrebno je samo provjeriti lin.nezavisnost. Zasto? Jer za bazu je potrebno dokazati da je lin.nezavisna i da je sustav izvodnica.
Na ovom zadnjem predavanju je prof jako lijepo objasnio:
ako je dimenzija recimo "n"
- sustav izvodnica moze imati najmanje "n" elemenata (znaci moze jedanako ili vise od toga), ako ima jednako elemenata potrebnoj e provjeriti samo lin.nezavisnost, ako ima vise elemenata od "n" onda ga je potrebno reducirati, znaci smanjiti ( izbacivanjem onih clanova koji su lin.zavisni s ostalima) sve dok ne zadovoljimo bazu odnosno dimenziju
- a lin.nezavisan sustav moze imati manje od "n" clanova ili jednako, ako ima jednako on je odmah i baza (i sustav izvodnica), a ko ima manje treba ga nadopuniti do baze odnosno zadovoljiti dimenziju.
Nadam se da sam dobro ukopcala stvari, ako grijesim neka me netko ispravi. Nadam se da ci biti od koristi. :)))
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="n.n."]sad više niš ne kužim. da li mi trebamo dokazivat prvo da je to baza ili je to pretpostavka zadatka pa ne moramo??[/quote]
Mi samo moramo ustanoviti za koji "t" ce on biti baza... znaci za sve realne brojeve on ce biti baza (jer cemo 0 podijeliti sa bilo kakvim brojem i dobit cemo 0, tj. lin ne zavisan sustav) samo za t=4 sustav ce imati parametarska rjesenja, jer na kraju onda dobijes 0=0, znaci za t=4 on je zavisan sustav, sto ne moze biti baza.
:))
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
Ja imam pitanje u vezi 3.zadatka?
Ne postoji nista laksi nacin dokazivanja sustava izvodnica, osim da uzmemo proizvoljni vektor i prikazemo ga kao lin kombinaciju preostalih?
I ako bi mogao netko objasniti 5.zadatak, molila bih lijepo?
Hvala.
Ja ovako razmisljam...Posto smo u trodimenzionalnom prostoru (sto zakljucujemo iz R^3= dim3) znamo da baza mora imati 3 člana (kao sto ima, u zadatku je vec zadana tročlana baza- jer da nije troclana, da ima vise clanova trebali bi reducirati do baze, izbacivati clanove koji su zavisni i tako doci do nezavisnog skupa).
Znaci, posto vec imamo tri clana, potrebno je samo provjeriti lin.nezavisnost. Zasto? Jer za bazu je potrebno dokazati da je lin.nezavisna i da je sustav izvodnica.
Na ovom zadnjem predavanju je prof jako lijepo objasnio:
ako je dimenzija recimo "n"
- sustav izvodnica moze imati najmanje "n" elemenata (znaci moze jedanako ili vise od toga), ako ima jednako elemenata potrebnoj e provjeriti samo lin.nezavisnost, ako ima vise elemenata od "n" onda ga je potrebno reducirati, znaci smanjiti ( izbacivanjem onih clanova koji su lin.zavisni s ostalima) sve dok ne zadovoljimo bazu odnosno dimenziju
- a lin.nezavisan sustav moze imati manje od "n" clanova ili jednako, ako ima jednako on je odmah i baza (i sustav izvodnica), a ko ima manje treba ga nadopuniti do baze odnosno zadovoljiti dimenziju.
Nadam se da sam dobro ukopcala stvari, ako grijesim neka me netko ispravi. Nadam se da ci biti od koristi.  )) ))
Added after 6 minutes:
| n.n. (napisa): | | sad više niš ne kužim. da li mi trebamo dokazivat prvo da je to baza ili je to pretpostavka zadatka pa ne moramo?? |
Mi samo moramo ustanoviti za koji "t" ce on biti baza... znaci za sve realne brojeve on ce biti baza (jer cemo 0 podijeliti sa bilo kakvim brojem i dobit cemo 0, tj. lin ne zavisan sustav) samo za t=4 sustav ce imati parametarska rjesenja, jer na kraju onda dobijes 0=0, znaci za t=4 on je zavisan sustav, sto ne moze biti baza.
 ) )
Added after 3 minutes:
Ja imam pitanje u vezi 3.zadatka?
Ne postoji nista laksi nacin dokazivanja sustava izvodnica, osim da uzmemo proizvoljni vektor i prikazemo ga kao lin kombinaciju preostalih?
I ako bi mogao netko objasniti 5.zadatak, molila bih lijepo?
Hvala.
|
|
| [Vrh] |
|
n.n.
Gost
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 14:11 sri, 20. 10. 2010 Naslov: Postano: 14:11 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="n.n."]Ovo je valjda točno za 3. zad:
Prema tvrdnji: svaki lin. nez. skup koji ima točno n elemenata je baza za V; mi zadani skup iz 3. zad reduciramo do lin nez. skupa s 4 elemenata (ak je moguće). i to onda automatski znači da je on baza, odnosno sustav izvodnica? ili sam neš pobrkala :lol:[/quote]
Tocno tako, bravo! Moguce je reducirati do 4 elementa, bez problema. Znaci pocnes tako da 2.vektor pokazes pomocu prvog, ako ej lin zavisan odbacis ga, ako ne ostavljas ga, tako isprobavas sve dok ne dobijes 4 vektora, ako ih dobijes prije nego sto uopce sve isprobas ne moras dalje isprobavati, al u ovom zadatku ces morati do kraja. :D
| n.n. (napisa): | Ovo je valjda točno za 3. zad:
Prema tvrdnji: svaki lin. nez. skup koji ima točno n elemenata je baza za V; mi zadani skup iz 3. zad reduciramo do lin nez. skupa s 4 elemenata (ak je moguće). i to onda automatski znači da je on baza, odnosno sustav izvodnica? ili sam neš pobrkala  |
Tocno tako, bravo! Moguce je reducirati do 4 elementa, bez problema. Znaci pocnes tako da 2.vektor pokazes pomocu prvog, ako ej lin zavisan odbacis ga, ako ne ostavljas ga, tako isprobavas sve dok ne dobijes 4 vektora, ako ih dobijes prije nego sto uopce sve isprobas ne moras dalje isprobavati, al u ovom zadatku ces morati do kraja. 
|
|
| [Vrh] |
|
travana
Forumaš(ica)

Pridružen/a: 22. 09. 2010. (17:12:41)
Postovi: (16)16
Spol: 
|
 Postano: 17:15 sri, 20. 10. 2010 Naslov: Postano: 17:15 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="frutabella"][quote="n.n."]Ovo je valjda točno za 3. zad:
Prema tvrdnji: svaki lin. nez. skup koji ima točno n elemenata je baza za V; mi zadani skup iz 3. zad reduciramo do lin nez. skupa s 4 elemenata (ak je moguće). i to onda automatski znači da je on baza, odnosno sustav izvodnica? ili sam neš pobrkala :lol:[/quote]
Tocno tako, bravo! Moguce je reducirati do 4 elementa, bez problema. Znaci pocnes tako da 2.vektor pokazes pomocu prvog, ako ej lin zavisan odbacis ga, ako ne ostavljas ga, tako isprobavas sve dok ne dobijes 4 vektora, ako ih dobijes prije nego sto uopce sve isprobas ne moras dalje isprobavati, al u ovom zadatku ces morati do kraja. :D[/quote]
hm, ja nisam morala do kraja. dobila sam da se prva 4 vec nemogu prikazati preko prethodnika, znaci nezavisni su i posto ih je 4 gotovo. il sam nes krivo racunala :?
[size=9][color=#999999]Added after 49 minutes:[/color][/size]
[quote="frutabella"]
I ako bi mogao netko objasniti 5.zadatak, molila bih lijepo?
Hvala.[/quote]
dimenzije tih prostora su jednake, jer je C u ovom slucaju prostor nad C sto takodjer znaci i da skalari smiju biti kompleksni te se svaki vektor iz C stvarno moze prikazati pomocu realne baze.
al nisam sigurna kako bih to tocno zapisala i jel to uopce dovoljno :D
| frutabella (napisa): | | n.n. (napisa): | Ovo je valjda točno za 3. zad:
Prema tvrdnji: svaki lin. nez. skup koji ima točno n elemenata je baza za V; mi zadani skup iz 3. zad reduciramo do lin nez. skupa s 4 elemenata (ak je moguće). i to onda automatski znači da je on baza, odnosno sustav izvodnica? ili sam neš pobrkala  |
Tocno tako, bravo! Moguce je reducirati do 4 elementa, bez problema. Znaci pocnes tako da 2.vektor pokazes pomocu prvog, ako ej lin zavisan odbacis ga, ako ne ostavljas ga, tako isprobavas sve dok ne dobijes 4 vektora, ako ih dobijes prije nego sto uopce sve isprobas ne moras dalje isprobavati, al u ovom zadatku ces morati do kraja.  |
hm, ja nisam morala do kraja. dobila sam da se prva 4 vec nemogu prikazati preko prethodnika, znaci nezavisni su i posto ih je 4 gotovo. il sam nes krivo racunala 
Added after 49 minutes:
| frutabella (napisa): |
I ako bi mogao netko objasniti 5.zadatak, molila bih lijepo?
Hvala. |
dimenzije tih prostora su jednake, jer je C u ovom slucaju prostor nad C sto takodjer znaci i da skalari smiju biti kompleksni te se svaki vektor iz C stvarno moze prikazati pomocu realne baze.
al nisam sigurna kako bih to tocno zapisala i jel to uopce dovoljno 
|
|
| [Vrh] |
|
toy.200
Forumaš(ica)

Pridružen/a: 28. 09. 2010. (14:45:47)
Postovi: (3)16
Spol: 
|
 Postano: 17:19 sri, 20. 10. 2010 Naslov: Postano: 17:19 sri, 20. 10. 2010 Naslov: |
    |
|
|
ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
sto s 4. i 5.?
ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
sto s 4. i 5.?
_________________
:]
|
|
| [Vrh] |
|
travana
Forumaš(ica)

Pridružen/a: 22. 09. 2010. (17:12:41)
Postovi: (16)16
Spol: 
|
 Postano: 17:34 sri, 20. 10. 2010 Naslov: Postano: 17:34 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="toy.200"]ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
[/quote]
da, naravno. uspjela sam nekako pobrkati koordinate vektora i krivo zbrojiti :D kad mi se ne da sve zapisivati :roll:
[quote="toy.200"]
sto s 4. i 5.?[/quote]
4. ima na forumu, a 5. sam gore napisala sto mislim al nisam sigurna.
| toy.200 (napisa): | ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
|
da, naravno. uspjela sam nekako pobrkati koordinate vektora i krivo zbrojiti  kad mi se ne da sve zapisivati kad mi se ne da sve zapisivati 
| toy.200 (napisa): |
sto s 4. i 5.? |
4. ima na forumu, a 5. sam gore napisala sto mislim al nisam sigurna.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 17:37 sri, 20. 10. 2010 Naslov: Postano: 17:37 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="toy.200"]ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
sto s 4. i 5.?[/quote]
i ja sam dobila...1,2,4,6 da su lin nezavisni... (ne znam kako je gore mislljeno da je odmah dobiveno...)
E super ovo za sustav izvodnica, a zamisli kak sam se ja tek raspisala kad sam sve htjela prikazazti kao lin komb...uzas! :D
Nadam se da sam skontala 5. ...vidjet cu kasnije..
Hvala!
| toy.200 (napisa): | ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
sto s 4. i 5.? |
i ja sam dobila...1,2,4,6 da su lin nezavisni... (ne znam kako je gore mislljeno da je odmah dobiveno...)
E super ovo za sustav izvodnica, a zamisli kak sam se ja tek raspisala kad sam sve htjela prikazazti kao lin komb...uzas! 
Nadam se da sam skontala 5. ...vidjet cu kasnije..
Hvala!
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:54 sri, 20. 10. 2010 Naslov: Postano: 18:54 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="toy.200"]ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
sto s 4. i 5.?[/quote]
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja.
| toy.200 (napisa): | ja sam dobila da su 1,2,4 i 6 lin nezavisni..
za pokazivanje da su sustav izvodnica, prikazete prva 4 kao lin. komb. nekog vektora v, i dobijete da se moze prikazati kao neki v.. sada, ako je taj skup od prva 4 vektora sustav izvodnica, onda ce i njegov nadskup od 6 vektora biti sustav izvodnica.. ugl. napisala sam se..
sto s 4. i 5.? |
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja.
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 19:00 sri, 20. 10. 2010 Naslov: pomoc mala :) Postano: 19:00 sri, 20. 10. 2010 Naslov: pomoc mala :) |
    |
|
|
ja se nadam da kad skinete sliku da cete sve vidjet dobro,uglavnom tu vam je peti zadatak
ja se nadam da kad skinete sliku da cete sve vidjet dobro,uglavnom tu vam je peti zadatak
_________________
tko rano rani,malo spava
| Description: |
| tu vam je peti zadatak rjesen... |
|
| Filesize: |
75.64 KB |
| Viewed: |
215 Time(s) |

|
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
travana
Forumaš(ica)

Pridružen/a: 22. 09. 2010. (17:12:41)
Postovi: (16)16
Spol: 
|
 Postano: 19:24 sri, 20. 10. 2010 Naslov: Postano: 19:24 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="frutabella"]
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja.[/quote]
da, ali prvo moras pokazati da je taj skup izvodnica, znaci u prvom dijelu ne mozes znati da su bas tih 4 medjusobno linearno nezavisni, dakle to bi bilo nagadjanje.
iako ja se izgubim u raspisivanju svaki put :roll:
| frutabella (napisa): |
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja. |
da, ali prvo moras pokazati da je taj skup izvodnica, znaci u prvom dijelu ne mozes znati da su bas tih 4 medjusobno linearno nezavisni, dakle to bi bilo nagadjanje.
iako ja se izgubim u raspisivanju svaki put 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 20:10 sri, 20. 10. 2010 Naslov: Postano: 20:10 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="travana"][quote="frutabella"]
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja.[/quote]
da, ali prvo moras pokazati da je taj skup izvodnica, znaci u prvom dijelu ne mozes znati da su bas tih 4 medjusobno linearno nezavisni, dakle to bi bilo nagadjanje.
iako ja se izgubim u raspisivanju svaki put :roll:[/quote]
da, u pravu si... znaci ipak moramo redom...
samo se osredotoci na to, da moras izbacivati dok ne dobijes trokut...ne zabporavi da si mozes premjestiti jednadzbe ((zamijenis im mjesta ili zamijenis stupce (bete stavis prije alfi itd.)- ovisi kako je najlakse))
| travana (napisa): | | frutabella (napisa): |
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja. |
da, ali prvo moras pokazati da je taj skup izvodnica, znaci u prvom dijelu ne mozes znati da su bas tih 4 medjusobno linearno nezavisni, dakle to bi bilo nagadjanje.
iako ja se izgubim u raspisivanju svaki put  |
da, u pravu si... znaci ipak moramo redom...
samo se osredotoci na to, da moras izbacivati dok ne dobijes trokut...ne zabporavi da si mozes premjestiti jednadzbe ((zamijenis im mjesta ili zamijenis stupce (bete stavis prije alfi itd.)- ovisi kako je najlakse))
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 20:25 sri, 20. 10. 2010 Naslov: Postano: 20:25 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="frutabella"][quote="travana"][quote="frutabella"]
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja.[/quote]
da, ali prvo moras pokazati da je taj skup izvodnica, znaci u prvom dijelu ne mozes znati da su bas tih 4 medjusobno linearno nezavisni, dakle to bi bilo nagadjanje.
iako ja se izgubim u raspisivanju svaki put :roll:[/quote]
da, u pravu si... znaci ipak moramo redom...
samo se osredotoci na to, da moras izbacivati dok ne dobijes trokut...ne zabporavi da si mozes premjestiti jednadzbe ((zamijenis im mjesta ili zamijenis stupce (bete stavis prije alfi itd.)- ovisi kako je najlakse))[/quote]
nigdje ne pise [b]prvo [/b]pokazi da je s.i nego pokazi da je s.i i reduciraj do baze...tako da pokazes da je baza,i u zadatku se pravis ''glup''ko da neznas da je baza i onda kazes da je nadskup baze s.i tako nesto
| frutabella (napisa): | | travana (napisa): | | frutabella (napisa): |
Za 3.: ako uzmes 1.,2.,4. i 6. vektor = najlakse prikazes lin kombinaciju, bez previse raspisivanja. |
da, ali prvo moras pokazati da je taj skup izvodnica, znaci u prvom dijelu ne mozes znati da su bas tih 4 medjusobno linearno nezavisni, dakle to bi bilo nagadjanje.
iako ja se izgubim u raspisivanju svaki put  |
da, u pravu si... znaci ipak moramo redom...
samo se osredotoci na to, da moras izbacivati dok ne dobijes trokut...ne zabporavi da si mozes premjestiti jednadzbe ((zamijenis im mjesta ili zamijenis stupce (bete stavis prije alfi itd.)- ovisi kako je najlakse)) |
nigdje ne pise prvo pokazi da je s.i nego pokazi da je s.i i reduciraj do baze...tako da pokazes da je baza,i u zadatku se pravis ''glup''ko da neznas da je baza i onda kazes da je nadskup baze s.i tako nesto
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
|














