| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 17:44 ned, 17. 10. 2010 Naslov: Zadatak iz 2. domaće zadaće Postano: 17:44 ned, 17. 10. 2010 Naslov: Zadatak iz 2. domaće zadaće |
    |
|
|
Odredite inverz funkcije [latex]f(x) = ch(-x^2 +4x - 3)[/latex] na području strogog pada.
Znam kako bih otprilike odredio inverz preko kompozicije funkcija, no problem mi je odrediti ''područje strogog pada''.
Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od [latex]<-\infty, 0][/latex], pa bi [latex]f(x) = ch(-x^2 +4x - 3)[/latex] strogo padala na svim dijelovima gdje je [latex]-x^2 +4x - 3[/latex] manji ili jednak nuli...
Da li ispravno razmišljam? Ako ne, ispravite me, ako da, kako bih to formalno napisao (npr. da je ovo zadatak na kolokviju).
Odredite inverz funkcije 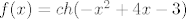 na području strogog pada. na području strogog pada.
Znam kako bih otprilike odredio inverz preko kompozicije funkcija, no problem mi je odrediti ''područje strogog pada''.
Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od 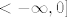 , pa bi , pa bi 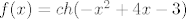 strogo padala na svim dijelovima gdje je strogo padala na svim dijelovima gdje je 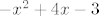 manji ili jednak nuli... manji ili jednak nuli...
Da li ispravno razmišljam? Ako ne, ispravite me, ako da, kako bih to formalno napisao (npr. da je ovo zadatak na kolokviju).
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:19 ned, 17. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće Postano: 18:19 ned, 17. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće |
    |
|
|
[quote="ceps"]Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od [latex]<-\infty, 0][/latex], pa bi [latex]f(x) = ch(-x^2 +4x - 3)[/latex] strogo padala na svim dijelovima gdje je [latex]-x^2 +4x - 3[/latex] manji ili jednak nuli...[/quote]
Dobro si krenuo, ali to nije dovoljno. :)
Vidimo [latex]-x^2 + 4 x - 3 = -(x - 1)(x - 3)[/latex] na intervalu [latex][3, +\infty \rangle[/latex] je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća [latex]\circ[/latex] padajuća = rastuća).
Promotrimo ova četiri intervala: [latex]\langle -\infty, 1][/latex], [latex][1, 2][/latex], [latex][2, 3][/latex] i [latex][3, +\infty \rangle[/latex]. Na 1. i 4. intervalu je [latex]-x^2 +4x - 3[/latex] nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća.
Lako vidimo da je fja f strogo padajuća samo na 1. i 3. intervalu. Dakle, interval strogog pada je [latex]\langle -\infty, 1] \cup [2, 3][/latex].
U to se dodatno možemo uvjeriti [url=http://www.wolframalpha.com/input/?i=Plot%28Cosh%28-x^2+%2B+4x+-+3%29%2C+{x%2C+0%2C+4}%29]slikom[/url]. :)
| ceps (napisa): | Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od 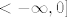 , pa bi , pa bi 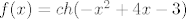 strogo padala na svim dijelovima gdje je strogo padala na svim dijelovima gdje je 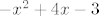 manji ili jednak nuli... manji ili jednak nuli... |
Dobro si krenuo, ali to nije dovoljno. 
Vidimo  na intervalu na intervalu 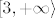 je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća  padajuća = rastuća). padajuća = rastuća).
Promotrimo ova četiri intervala: 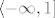 , , 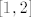 , , 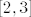 i i 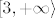 . Na 1. i 4. intervalu je . Na 1. i 4. intervalu je 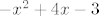 nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća. nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća.
Lako vidimo da je fja f strogo padajuća samo na 1. i 3. intervalu. Dakle, interval strogog pada je 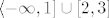 . .
U to se dodatno možemo uvjeriti slikom. 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 21:37 sri, 20. 10. 2010 Naslov: Postano: 21:37 sri, 20. 10. 2010 Naslov: |
    |
|
|
Imam pitanje, prvi zadatak iz dz2, skroz lagan i onda kad sam pokusala rijesiti na oba nacina, slika funkcije ispadne skroz drukcija.
sa skicom slika funkcije je [4,10> , a racunski [-9/4, 10> ????????
I onda prelistam biljeznicu i vidim da samo skroz na pocetku vjezbi imali isti zadatak (sa skicom odrediti sliku kvad.funkcije, i onda skroz kasnije smo istu tu funkciju odredili racunski i dobili smo razlicite rezultate)
Zbunjola cista.
Sa skice je vrlo ocito, al zasto racunski nije...
racunski dobijem dva intervala [-9/4, 4] i [-9/4, 10> rekli smo unija svega je slika funkcije.
Gdje brljam?
Imam pitanje, prvi zadatak iz dz2, skroz lagan i onda kad sam pokusala rijesiti na oba nacina, slika funkcije ispadne skroz drukcija.
sa skicom slika funkcije je [4,10> , a racunski [-9/4, 10> ????????
I onda prelistam biljeznicu i vidim da samo skroz na pocetku vjezbi imali isti zadatak (sa skicom odrediti sliku kvad.funkcije, i onda skroz kasnije smo istu tu funkciju odredili racunski i dobili smo razlicite rezultate)
Zbunjola cista.
Sa skice je vrlo ocito, al zasto racunski nije...
racunski dobijem dva intervala [-9/4, 4] i [-9/4, 10> rekli smo unija svega je slika funkcije.
Gdje brljam?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:00 sri, 20. 10. 2010 Naslov: Postano: 22:00 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="frutabella"]Gdje brljam?[/quote]
Teško je za reći dok malo detaljnije ne napišeš kako si skicirala graf funkcije.
Kako ti je sa skice očito da je slika [4,10>? Gdje ti pobjegne dio ispod 4? Nultočke su 2 i 5, minimum funkcije je na pola puta, znači za x=3.5, tj. vrijednost minimuma je -9/4. Predznak uz x je pozitivan pa je parabola okrenuta prema dole sa tjemenom u točki (3.5,-9/4). Zašto tebi pobjegne minimum sve do 4?
| frutabella (napisa): | | Gdje brljam? |
Teško je za reći dok malo detaljnije ne napišeš kako si skicirala graf funkcije.
Kako ti je sa skice očito da je slika [4,10>? Gdje ti pobjegne dio ispod 4? Nultočke su 2 i 5, minimum funkcije je na pola puta, znači za x=3.5, tj. vrijednost minimuma je -9/4. Predznak uz x je pozitivan pa je parabola okrenuta prema dole sa tjemenom u točki (3.5,-9/4). Zašto tebi pobjegne minimum sve do 4?
_________________
The Dude Abides
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 22:11 sri, 20. 10. 2010 Naslov: Postano: 22:11 sri, 20. 10. 2010 Naslov: |
    |
|
|
[quote="goranm"][quote="frutabella"]Gdje brljam?[/quote]
Teško je za reći dok malo detaljnije ne napišeš kako si skicirala graf funkcije.
Kako ti je sa skice očito da je slika [4,10>? Gdje ti pobjegne dio ispod 4? Nultočke su 2 i 5, minimum funkcije je na pola puta, znači za x=3.5, tj. vrijednost minimuma je -9/4. Predznak uz x je pozitivan pa je parabola okrenuta prema dole sa tjemenom u točki (3.5,-9/4). Zašto tebi pobjegne minimum sve do 4?[/quote]
Ma da, skicu sam pogresno iščitala, logicno mi je i sa skice da je rjesenje od <-9/4, 10], al sam pogresno pofarbala dio (ono sto smo radili, pa preslikala pogresno na y) ...
Hvala ti!
| goranm (napisa): | | frutabella (napisa): | | Gdje brljam? |
Teško je za reći dok malo detaljnije ne napišeš kako si skicirala graf funkcije.
Kako ti je sa skice očito da je slika [4,10>? Gdje ti pobjegne dio ispod 4? Nultočke su 2 i 5, minimum funkcije je na pola puta, znači za x=3.5, tj. vrijednost minimuma je -9/4. Predznak uz x je pozitivan pa je parabola okrenuta prema dole sa tjemenom u točki (3.5,-9/4). Zašto tebi pobjegne minimum sve do 4? |
Ma da, skicu sam pogresno iščitala, logicno mi je i sa skice da je rjesenje od ←9/4, 10], al sam pogresno pofarbala dio (ono sto smo radili, pa preslikala pogresno na y) ...
Hvala ti!
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 16:11 čet, 21. 10. 2010 Naslov: Postano: 16:11 čet, 21. 10. 2010 Naslov: |
    |
|
|
Pa ja bih. :) (Ako pod tablicom misliš na gledanje za svaki faktor kad je veći od nula, a kad je manji.)
Evo, da pomognem da vidiš jel ti rješenje dobro. Dakle,dobila si već da je [latex]x>0[/latex] (zbog logaritma) i [latex]x\neq 2[/latex] (zbog nazivnika).
Sad te zanima kad je taj cijeli razlomak veći ili jednak [latex]0[/latex]. E, sad, [latex]2^x-16[/latex] je veće ili jednako [latex]0[/latex] za [latex]x\geq 4[/latex], a manje od [latex]0[/latex] za [latex]x<4[/latex]. [latex](\log_2 (x)-1)^3[/latex] ima isti predznak kao i [latex]\log_2 (x) -1[/latex], a to je veće ili jednako [latex]0[/latex] za [latex]x>2[/latex] (već smo utvrdili da [latex]x[/latex] ne može biti [latex]2[/latex]), a negativno u ostalim slučajevima. Također, [latex]4^x-3\cdot 2^x-4=(2^x+1)(2^x-4)[/latex] je negativno za [latex]x<2[/latex], a pozitivno inače. Naravno, uzimamo u obzir da [latex]x>0[/latex] i [latex]x\neq 2[/latex].
Stoga vidimo da imamo dvije "upitne" točke: [latex]2[/latex] i [latex]4[/latex]. Za [latex]0<x<2[/latex] cijeli izraz je negativan (obje zagrade u brojniku su negativne, kao i nazivnik). [latex]2<x<4[/latex] također nije u redu: prva zagrada u brojniku je negativna, druga pozitivna, a nazivnik je isto pozitivan. Stoga je produkt opet negativan. Naposljetku, [latex]x\geq 4[/latex] je u redu - svi su izrazi nenegativni.
I to bi bilo to: i WolframAlpha se [url=http://www.wolframalpha.com/input/?i=solve+%282%5Ex-16%29%2A%28log+x+%2F+log+2+-1%29%5E3%2F%284%5Ex-3%2A2%5Ex-4%29%3E%3D0]slaže[/url]. :)
Pa ja bih.  (Ako pod tablicom misliš na gledanje za svaki faktor kad je veći od nula, a kad je manji.) (Ako pod tablicom misliš na gledanje za svaki faktor kad je veći od nula, a kad je manji.)
Evo, da pomognem da vidiš jel ti rješenje dobro. Dakle,dobila si već da je 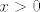 (zbog logaritma) i (zbog logaritma) i 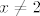 (zbog nazivnika). (zbog nazivnika).
Sad te zanima kad je taj cijeli razlomak veći ili jednak  . E, sad, . E, sad, 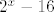 je veće ili jednako je veće ili jednako  za za 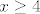 , a manje od , a manje od  za za 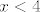 . . 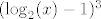 ima isti predznak kao i ima isti predznak kao i 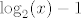 , a to je veće ili jednako , a to je veće ili jednako  za za 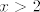 (već smo utvrdili da (već smo utvrdili da  ne može biti ne može biti  ), a negativno u ostalim slučajevima. Također, ), a negativno u ostalim slučajevima. Također, 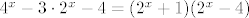 je negativno za je negativno za 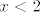 , a pozitivno inače. Naravno, uzimamo u obzir da , a pozitivno inače. Naravno, uzimamo u obzir da 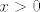 i i 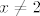 . .
Stoga vidimo da imamo dvije "upitne" točke:  i i 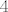 . Za . Za 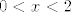 cijeli izraz je negativan (obje zagrade u brojniku su negativne, kao i nazivnik). cijeli izraz je negativan (obje zagrade u brojniku su negativne, kao i nazivnik). 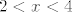 također nije u redu: prva zagrada u brojniku je negativna, druga pozitivna, a nazivnik je isto pozitivan. Stoga je produkt opet negativan. Naposljetku, također nije u redu: prva zagrada u brojniku je negativna, druga pozitivna, a nazivnik je isto pozitivan. Stoga je produkt opet negativan. Naposljetku, 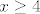 je u redu - svi su izrazi nenegativni. je u redu - svi su izrazi nenegativni.
I to bi bilo to: i WolframAlpha se slaže. 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 19:28 čet, 21. 10. 2010 Naslov: Postano: 19:28 čet, 21. 10. 2010 Naslov: |
    |
|
|
[quote="pedro"]hvala ti sad mi je puno jasnije :))
[size=9][color=#999999]Added after 55 minutes:[/color][/size]
zadana mi je funkcija:
[latex]f(x)=\sqrt{2^ \cos x}[/latex]
i traži se da odredim [latex]f^{-1}([1,3>)[/latex]
prvo kaj trebam napravit je da napravim kompoziciju.
to sam ovak napravila:
[latex]f(x)={f_1}\circ{f_2}\circ{f_3}[/latex]
[latex]f_1=\sqrt{x}[/latex]
[latex]f_2=2^x[/latex]
[latex]f_3=cos x[/latex]
jel to uredu zasad?
i sad trebam odredit
[latex]f([1,3>)=f_1(f_2(f_3([1,3>))[/latex]
i počnem od [latex]f_3([1,3>)[/latex]
a [latex]f_3=cos x[/latex]
kako cos nije definiran nigdje osim [latex][-1,1][/latex] kako da nađem prasliku? možda sam pogrješila negdje u ovim koracima.[/quote]
Mislim da ne mozes staviti domenu za f da je [1.3>, to je domena za prasliku,a kod funkcije ce domena biti prvo domena 3.komp.funkcije ----> [b]GRESKA!!!! DOMENA CE BITI DOMENA SVIH TRIJU FUNKCIJA (presjek uvjeta za pojedinacne funkcije)[/b] , znaci domena od cos(x) i 2^x je R, a domena korijena x>0 sto znaci slika je presjek tih domena, a to je <0,+besk>], ta slika ce biti onda domena za sljedecu kompoziciju, tj. f(x)=f1(f2(<0, +besk>)... onda slika f2 ce biti domena za f1 i tako dodjes do slike za f(x). (nadam se da sam se dobro izrazila, sad mi je to malo iz glave, nemam na papiru pa mi je teze).
A da ne treba to odrediti inverz mozda ? Ili ipak prasliku?
[size=9][color=#999999]Added after 8 minutes:[/color][/size]
[quote="goranm"][quote="frutabella"]Gdje brljam?[/quote]
Teško je za reći dok malo detaljnije ne napišeš kako si skicirala graf funkcije.
Kako ti je sa skice očito da je slika [4,10>? Gdje ti pobjegne dio ispod 4? Nultočke su 2 i 5, minimum funkcije je na pola puta, znači za x=3.5, tj. vrijednost minimuma je -9/4. Predznak uz x je pozitivan pa je parabola okrenuta prema dole sa tjemenom u točki (3.5,-9/4). Zašto tebi pobjegne minimum sve do 4?[/quote]
Znas sta? Parabola sve ok nacrtana, dobro sam nacrtala, i onda sam oznacila gdje interval sijece parabolu ( znaci kad povucemo okomicu nad prvim br.iz intervala i tamo gdje sjece parabolu---vidimo gdje preslika na y-osi) i preslika na broj 4 na y-osi, isto tako drugi broj se preslika na 10 na y-osi, pa sam tako zakljucila da je to interval. Zar treba uvijek gledati od tjemena pa do najveceg broja na y-osi? Malo me to zbunjuje, al mislim da ce btii tako.
| pedro (napisa): | hvala ti sad mi je puno jasnije  ) )
Added after 55 minutes:
zadana mi je funkcija:
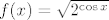
i traži se da odredim 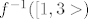
prvo kaj trebam napravit je da napravim kompoziciju.
to sam ovak napravila:
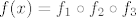

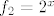
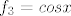
jel to uredu zasad?
i sad trebam odredit
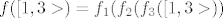
i počnem od 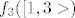
a 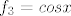
kako cos nije definiran nigdje osim 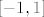 kako da nađem prasliku? možda sam pogrješila negdje u ovim koracima. kako da nađem prasliku? možda sam pogrješila negdje u ovim koracima. |
Mislim da ne mozes staviti domenu za f da je [1.3>, to je domena za prasliku,a kod funkcije ce domena biti prvo domena 3.komp.funkcije ----> GRESKA!!!! DOMENA CE BITI DOMENA SVIH TRIJU FUNKCIJA (presjek uvjeta za pojedinacne funkcije) , znaci domena od cos(x) i 2^x je R, a domena korijena x>0 sto znaci slika je presjek tih domena, a to je <0,+besk>], ta slika ce biti onda domena za sljedecu kompoziciju, tj. f(x)=f1(f2(<0, +besk>)... onda slika f2 ce biti domena za f1 i tako dodjes do slike za f(x). (nadam se da sam se dobro izrazila, sad mi je to malo iz glave, nemam na papiru pa mi je teze).
A da ne treba to odrediti inverz mozda ? Ili ipak prasliku?
Added after 8 minutes:
| goranm (napisa): | | frutabella (napisa): | | Gdje brljam? |
Teško je za reći dok malo detaljnije ne napišeš kako si skicirala graf funkcije.
Kako ti je sa skice očito da je slika [4,10>? Gdje ti pobjegne dio ispod 4? Nultočke su 2 i 5, minimum funkcije je na pola puta, znači za x=3.5, tj. vrijednost minimuma je -9/4. Predznak uz x je pozitivan pa je parabola okrenuta prema dole sa tjemenom u točki (3.5,-9/4). Zašto tebi pobjegne minimum sve do 4? |
Znas sta? Parabola sve ok nacrtana, dobro sam nacrtala, i onda sam oznacila gdje interval sijece parabolu ( znaci kad povucemo okomicu nad prvim br.iz intervala i tamo gdje sjece parabolu—vidimo gdje preslika na y-osi) i preslika na broj 4 na y-osi, isto tako drugi broj se preslika na 10 na y-osi, pa sam tako zakljucila da je to interval. Zar treba uvijek gledati od tjemena pa do najveceg broja na y-osi? Malo me to zbunjuje, al mislim da ce btii tako.
Zadnja promjena: frutabella; 19:10 ned, 24. 10. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 19:48 čet, 21. 10. 2010 Naslov: Postano: 19:48 čet, 21. 10. 2010 Naslov: |
    |
|
|
pa stvar je u tome da za prasliku gledam po kodomeni a ne domeni, brijem da se inverz ne traži jer se inverz traži od cijele funkcije a ne neki interval.
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="frutabella"]
Znas sta? Parabola sve ok nacrtana, dobro sam nacrtala, i onda sam oznacila gdje interval sijece parabolu ( znaci kad povucemo okomicu nad prvim br.iz intervala i tamo gdje sjece parabolu---vidimo gdje preslika na y-osi) i preslika na broj 4 na y-osi, isto tako drugi broj se preslika na 10 na y-osi, pa sam tako zakljucila da je to interval. Zar treba uvijek gledati od tjemena pa do najveceg broja na y-osi? Malo me to zbunjuje, al mislim da ce btii tako.[/quote]
[url]https://mail.google.com/mail/?ui=2&ik=7458503e18&view=att&th=12bc07d811c17826&attid=0.1&disp=inline&zw[/url]
pogledaj ovu sliku. gledaš po paraboli..
zato i trebamo crtat grafove, a ne samo uvrstit brojeve u funkciju
pa stvar je u tome da za prasliku gledam po kodomeni a ne domeni, brijem da se inverz ne traži jer se inverz traži od cijele funkcije a ne neki interval.
Added after 6 minutes:
| frutabella (napisa): |
Znas sta? Parabola sve ok nacrtana, dobro sam nacrtala, i onda sam oznacila gdje interval sijece parabolu ( znaci kad povucemo okomicu nad prvim br.iz intervala i tamo gdje sjece parabolu—vidimo gdje preslika na y-osi) i preslika na broj 4 na y-osi, isto tako drugi broj se preslika na 10 na y-osi, pa sam tako zakljucila da je to interval. Zar treba uvijek gledati od tjemena pa do najveceg broja na y-osi? Malo me to zbunjuje, al mislim da ce btii tako. |
https://mail.google.com/mail/?ui=2&ik=7458503e18&view=att&th=12bc07d811c17826&attid=0.1&disp=inline&zw
pogledaj ovu sliku. gledaš po paraboli..
zato i trebamo crtat grafove, a ne samo uvrstit brojeve u funkciju
|
|
| [Vrh] |
|
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:26 čet, 21. 10. 2010 Naslov: Postano: 21:26 čet, 21. 10. 2010 Naslov: |
    |
|
|
Da, nije baš potpuno trivijalan zadatak: pogledaj hintove u trećem i četvrtom postu [url=http://degiorgi.math.hr/forum/viewtopic.php?t=13930]tu[/url]. Ako se ne varam, potkrao mi se tamo tipfeler, treba pisati [latex]f(t+\frac{\pi}{2})[/latex] umjesto [latex]f(\frac{\pi}{2})[/latex] ili tako nešto.
Ne-sasvim-točno rješenje možeš vidjeti [url=http://answers.yahoo.com/question/index?qid=20091129090651AAXQXJF]tu[/url]. Greška (dosta očita :)) je u četvrtom redu, ali zaključak i dalje vrijedi, samo treba izmijeniti neke brojeve. Za preciznost, treba se još malo pomučiti, ali je poanta i veći dio izvoda tamo, dalje je samo tehnički rad.
Reci ako treba još pomoći.
Da, nije baš potpuno trivijalan zadatak: pogledaj hintove u trećem i četvrtom postu tu. Ako se ne varam, potkrao mi se tamo tipfeler, treba pisati 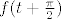 umjesto umjesto 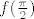 ili tako nešto. ili tako nešto.
Ne-sasvim-točno rješenje možeš vidjeti tu. Greška (dosta očita  ) je u četvrtom redu, ali zaključak i dalje vrijedi, samo treba izmijeniti neke brojeve. Za preciznost, treba se još malo pomučiti, ali je poanta i veći dio izvoda tamo, dalje je samo tehnički rad. ) je u četvrtom redu, ali zaključak i dalje vrijedi, samo treba izmijeniti neke brojeve. Za preciznost, treba se još malo pomučiti, ali je poanta i veći dio izvoda tamo, dalje je samo tehnički rad.
Reci ako treba još pomoći.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:00 pet, 22. 10. 2010 Naslov: Postano: 17:00 pet, 22. 10. 2010 Naslov: |
    |
|
|
Čini ti se da je lakši nego što jest. :) Moram, doduše, priznati da ne mogu baš shvatiti što si napravila. :D Specifično, mislim da imaš jednu grešku (kad uvrštavaš [latex]x+T[/latex] umjesto [latex]x[/latex], ne dobivaš [latex]\sin(x^2+T)[/latex], nego [latex]\sin((x+T)^2)[/latex].
Također, ne znam što znači da si stavila da je period [latex]2\pi[/latex]. Zapravo, mislim da znam. :) Ti si, uz ovu prethodnu grešku, "pokazala" da je [latex]2\pi[/latex] sasvim legalan period. :) Ali, da, funkcija nije periodična, što znači da ćeš trebati pokazati da niti jedan [latex]T[/latex] ne može biti period, a ne neki određeni [latex]T[/latex].
Mislim da smo mi na demonstraturama riješili stvar uvrštavanjem [latex]x=0[/latex], [latex]x=\sqrt{\displaystyle\frac{\pi}{2}}[/latex] i [latex]x=\sqrt{\pi}[/latex], ali u svakom slučaju nije pretjerano lagano. :) Probaj, pa reci ako budeš htjela pomoć/neke korake rješenja.
Čini ti se da je lakši nego što jest.  Moram, doduše, priznati da ne mogu baš shvatiti što si napravila. Moram, doduše, priznati da ne mogu baš shvatiti što si napravila.  Specifično, mislim da imaš jednu grešku (kad uvrštavaš Specifično, mislim da imaš jednu grešku (kad uvrštavaš 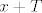 umjesto umjesto  , ne dobivaš , ne dobivaš 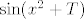 , nego , nego 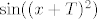 . .
Također, ne znam što znači da si stavila da je period 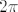 . Zapravo, mislim da znam. . Zapravo, mislim da znam.  Ti si, uz ovu prethodnu grešku, "pokazala" da je Ti si, uz ovu prethodnu grešku, "pokazala" da je 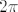 sasvim legalan period. sasvim legalan period.  Ali, da, funkcija nije periodična, što znači da ćeš trebati pokazati da niti jedan Ali, da, funkcija nije periodična, što znači da ćeš trebati pokazati da niti jedan  ne može biti period, a ne neki određeni ne može biti period, a ne neki određeni  . .
Mislim da smo mi na demonstraturama riješili stvar uvrštavanjem  , , 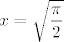 i i 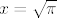 , ali u svakom slučaju nije pretjerano lagano. , ali u svakom slučaju nije pretjerano lagano.  Probaj, pa reci ako budeš htjela pomoć/neke korake rješenja. Probaj, pa reci ako budeš htjela pomoć/neke korake rješenja.
|
|
| [Vrh] |
|
|










