| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 16:26 sub, 23. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće Postano: 16:26 sub, 23. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće |
    |
|
|
[quote="pmli"][quote="ceps"]Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od [latex]<-\infty, 0][/latex], pa bi [latex]f(x) = ch(-x^2 +4x - 3)[/latex] strogo padala na svim dijelovima gdje je [latex]-x^2 +4x - 3[/latex] manji ili jednak nuli...[/quote]
Dobro si krenuo, ali to nije dovoljno. :)
Vidimo [latex]-x^2 + 4 x - 3 = -(x - 1)(x - 3)[/latex] na intervalu [latex][3, +\infty \rangle[/latex] je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća [latex]\circ[/latex] padajuća = rastuća).
Promotrimo ova četiri intervala: [latex]\langle -\infty, 1][/latex], [latex][1, 2][/latex], [latex][2, 3][/latex] i [latex][3, +\infty \rangle[/latex]. Na 1. i 4. intervalu je [latex]-x^2 +4x - 3[/latex] nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća.
Lako vidimo da je fja f strogo padajuća samo na 1. i 3. intervalu. Dakle, interval strogog pada je [latex]\langle -\infty, 1] \cup [2, 3][/latex].
U to se dodatno možemo uvjeriti [url=http://www.wolframalpha.com/input/?i=Plot%28Cosh%28-x^2+%2B+4x+-+3%29%2C+{x%2C+0%2C+4}%29]slikom[/url]. :)[/quote]
Ako sam ja dobro prokontala:
na negativnom dijelu parabole koji je ujedno strogo padajuc [3,+besk.] djelujemo strogo padajucom ch funkcijom,
a na pozitivnom dijelu parabole koji je ujdeno strogo padajuc, djelujemo strogo rastucom ch funkcijom (padajuca o rastuca =padajuca)
UGL: (kak je kompliciranoooo)
NA NEGATIVNIIM DJELOVIMA PARABOLE DJELUJEMO PADAJUCOM CH FUNK., A NA POZITIVNIM DJELOVIMA PARABOLE DJELUJEMO RASTUCOM CH FUNKCIJOM.
| pmli (napisa): | | ceps (napisa): | Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od 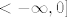 , pa bi , pa bi 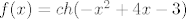 strogo padala na svim dijelovima gdje je strogo padala na svim dijelovima gdje je 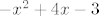 manji ili jednak nuli... manji ili jednak nuli... |
Dobro si krenuo, ali to nije dovoljno. 
Vidimo  na intervalu na intervalu 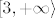 je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća  padajuća = rastuća). padajuća = rastuća).
Promotrimo ova četiri intervala: 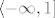 , , 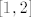 , , 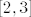 i i 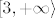 . Na 1. i 4. intervalu je . Na 1. i 4. intervalu je 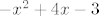 nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća. nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća.
Lako vidimo da je fja f strogo padajuća samo na 1. i 3. intervalu. Dakle, interval strogog pada je 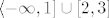 . .
U to se dodatno možemo uvjeriti slikom.  |
Ako sam ja dobro prokontala:
na negativnom dijelu parabole koji je ujedno strogo padajuc [3,+besk.] djelujemo strogo padajucom ch funkcijom,
a na pozitivnom dijelu parabole koji je ujdeno strogo padajuc, djelujemo strogo rastucom ch funkcijom (padajuca o rastuca =padajuca)
UGL: (kak je kompliciranoooo)
NA NEGATIVNIIM DJELOVIMA PARABOLE DJELUJEMO PADAJUCOM CH FUNK., A NA POZITIVNIM DJELOVIMA PARABOLE DJELUJEMO RASTUCOM CH FUNKCIJOM.
|
|
| [Vrh] |
|
Sinuhe
Forumaš(ica)
Pridružen/a: 05. 08. 2010. (21:55:23)
Postovi: (6)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
 Postano: 11:23 ned, 24. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće Postano: 11:23 ned, 24. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće |
    |
|
|
[quote="pmli"][quote="ceps"]Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od [latex]<-\infty, 0][/latex], pa bi [latex]f(x) = ch(-x^2 +4x - 3)[/latex] strogo padala na svim dijelovima gdje je [latex]-x^2 +4x - 3[/latex] manji ili jednak nuli...[/quote]
Dobro si krenuo, ali to nije dovoljno. :)
Vidimo [latex]-x^2 + 4 x - 3 = -(x - 1)(x - 3)[/latex] na intervalu [latex][3, +\infty \rangle[/latex] je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća [latex]\circ[/latex] padajuća = rastuća).
Promotrimo ova četiri intervala: [latex]\langle -\infty, 1][/latex], [latex][1, 2][/latex], [latex][2, 3][/latex] i [latex][3, +\infty \rangle[/latex]. Na 1. i 4. intervalu je [latex]-x^2 +4x - 3[/latex] nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća.
Lako vidimo da je fja f strogo padajuća samo na 1. i 3. intervalu. Dakle, interval strogog pada je [latex]\langle -\infty, 1] \cup [2, 3][/latex].
U to se dodatno možemo uvjeriti [url=http://www.wolframalpha.com/input/?i=Plot%28Cosh%28-x^2+%2B+4x+-+3%29%2C+{x%2C+0%2C+4}%29]slikom[/url]. :)[/quote]
hmm..ako je cosh padajuci na intervalu <-00,o], a f(x) je tu padajuca zar to ne bi trebala biti rastuca( padajuca i padajuca) ? [0,1] ide padajuca i rastuca = padajuca, [1,2]rastuca i rastuca = rastuca, [2,3] padajuca i rastuca = padajuca i ono dalje isto rastuca i padajuca = padajuca?
negdje griješim ?
| pmli (napisa): | | ceps (napisa): | Neko moje razmišljanje je bilo da funkcija kosinus hiperbolni strogo pada na intervalu od 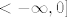 , pa bi , pa bi 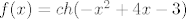 strogo padala na svim dijelovima gdje je strogo padala na svim dijelovima gdje je 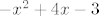 manji ili jednak nuli... manji ili jednak nuli... |
Dobro si krenuo, ali to nije dovoljno. 
Vidimo  na intervalu na intervalu 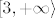 je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća je strogo padajuća i postiže nepozitivne vrijednosti, ali kad na nju djelujemo kosinusom hiperbolnim dobivamo strogo rastuću fju (padajuća  padajuća = rastuća). padajuća = rastuća).
Promotrimo ova četiri intervala: 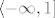 , , 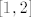 , , 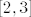 i i 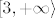 . Na 1. i 4. intervalu je . Na 1. i 4. intervalu je 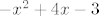 nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća. nepozitivno, na 2. i 3. nenegativno, na 1. i 2. strogo rastuća, na 3. i 4. strogo padajuća.
Lako vidimo da je fja f strogo padajuća samo na 1. i 3. intervalu. Dakle, interval strogog pada je 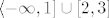 . .
U to se dodatno možemo uvjeriti slikom.  |
hmm..ako je cosh padajuci na intervalu ←00,o], a f(x) je tu padajuca zar to ne bi trebala biti rastuca( padajuca i padajuca) ? [0,1] ide padajuca i rastuca = padajuca, [1,2]rastuca i rastuca = rastuca, [2,3] padajuca i rastuca = padajuca i ono dalje isto rastuca i padajuca = padajuca?
negdje griješim ?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:47 ned, 24. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće Postano: 12:47 ned, 24. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće |
    |
|
|
[quote="kobila krsto"]hmm..ako je cosh padajuci na intervalu <-00,o], a f(x) je tu padajuca zar to ne bi trebala biti [b]rastuca[/b]( [b]padajuca[/b] i [b]padajuca[/b]) ? [0,1] ide [b]padajuca[/b] i [b]rastuca[/b] = [b]padajuca[/b], [1,2][b]rastuca[/b] i [b]rastuca[/b] = [b]rastuca[/b], [2,3] [b]padajuca[/b] i [b]rastuca[/b] = [b]padajuca[/b] i ono dalje isto [b]rastuca[/b] i [b]padajuca[/b] = [b]padajuca[/b]?[/quote]
:stars:
Možeš li, lijepo te molim, objasniti što je tu rastuće, a što padajuće? :)
| kobila krsto (napisa): | | hmm..ako je cosh padajuci na intervalu ←00,o], a f(x) je tu padajuca zar to ne bi trebala biti rastuca( padajuca i padajuca) ? [0,1] ide padajuca i rastuca = padajuca, [1,2]rastuca i rastuca = rastuca, [2,3] padajuca i rastuca = padajuca i ono dalje isto rastuca i padajuca = padajuca? |

Možeš li, lijepo te molim, objasniti što je tu rastuće, a što padajuće? 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 12:51 ned, 24. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće Postano: 12:51 ned, 24. 10. 2010 Naslov: Re: Zadatak iz 2. domaće zadaće |
    |
|
|
[quote="kobila krsto"]
hmm..ako je cosh padajuci na intervalu <-00,o], a f(x) je tu padajuca zar to ne bi trebala biti rastuca( padajuca i padajuca) ? [0,1] ide padajuca i rastuca = padajuca, [1,2]rastuca i rastuca = rastuca, [2,3] padajuca i rastuca = padajuca i ono dalje isto rastuca i padajuca = padajuca?
negdje griješim ?[/quote]
Za pocetak, f(x) nije padajuca na intervalu <-besk, 0> :wink:
| kobila krsto (napisa): |
hmm..ako je cosh padajuci na intervalu ←00,o], a f(x) je tu padajuca zar to ne bi trebala biti rastuca( padajuca i padajuca) ? [0,1] ide padajuca i rastuca = padajuca, [1,2]rastuca i rastuca = rastuca, [2,3] padajuca i rastuca = padajuca i ono dalje isto rastuca i padajuca = padajuca?
negdje griješim ? |
Za pocetak, f(x) nije padajuca na intervalu ←besk, 0> 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 19:24 ned, 24. 10. 2010 Naslov: Postano: 19:24 ned, 24. 10. 2010 Naslov: |
    |
|
|
[quote="Tomislav"]Znaci imas sljedece: [latex]f(x)=-x^2 -4x+5 -> -y=x^2+4x+4-9 -> 9-y=(x+2)^2 -> \sqrt{9-y}-2=x[/latex],
pa je inverz od [latex]f=g(x)=\sqrt{9-x} -2[/latex][/quote]
fala...skuzio sam :)
a 12.zadatak,kako se to sluzbeno dokaze,mislim ocito je da su to sve rastuce jer u a)zadatku eksponent je 1,3,5,7...
a u b)zadatku 2,4,6,8...
pa neka netko ako moze da sluzbeni dokaz za to...fala
ista stvar i za 13.zadatak,neznam kak bi to dokazao "sluzbeno"
jer smo mi to tako rekli na vjezbama...pa ako ko moze dat neki dokaz...
| Tomislav (napisa): | Znaci imas sljedece: 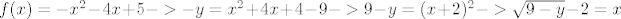 , ,
pa je inverz od 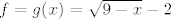 |
fala...skuzio sam 
a 12.zadatak,kako se to sluzbeno dokaze,mislim ocito je da su to sve rastuce jer u a)zadatku eksponent je 1,3,5,7...
a u b)zadatku 2,4,6,8...
pa neka netko ako moze da sluzbeni dokaz za to...fala
ista stvar i za 13.zadatak,neznam kak bi to dokazao "sluzbeno"
jer smo mi to tako rekli na vjezbama...pa ako ko moze dat neki dokaz...
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Linadus
Forumaš(ica)
Pridružen/a: 07. 09. 2010. (12:57:28)
Postovi: (2C)16
|
|
| [Vrh] |
|
|











