| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:44 čet, 21. 10. 2010 Naslov: Postano: 22:44 čet, 21. 10. 2010 Naslov: |
    |
|
|
1.b Kritično mjesto je [latex]\{ (x, y) : x^2 - 4 y = 0 \}[/latex] (a.k.a. parabola). U ostalim točkama je fja definirana, neprekidna, dakle bla, [size=9]bla,[/size] [size=7]bla...[/size]
Primjetimo da je [latex]\displaystyle \lim_{(x, y) \to (x_0, y_0)} \frac{2 x + y}{x^2 - 4y}[/latex] (za [latex](x_0, y_0)[/latex] td. [latex]x_0^2 -4 y_0 = 0[/latex]) oblika [latex]\displaystyle \left( \frac{2 x_0 + y_0}{0} \right)[/latex]. To znači da taj limes divergira ako je [latex]2 x_0 + y_0 \neq 0[/latex]. Tako nam se interesantan skup smanjuje na dvije točke: [latex](0, 0)[/latex] i [latex](-8, 16)[/latex] (rješenja sustava [latex]\left\{ \begin{array}{l}
2 x + y = 0 \\
x^2 - 4 y = 0
\end{array} \right.[/latex]). Može se pokazati da fja nema limes niti u jednoj od tih točaka.
Za točku (0,0) možemo promotriti kad [spoiler][latex](x, 0) \to (0, 0)[/latex][/spoiler] a za (-8,16) [spoiler][latex](x, 16) \to (-8, 16)[/latex] i [latex](-8, y) \to (-8, 16)[/latex][/spoiler]
1.c Na vrlo sličan način kao gore dođemo do točke (0,0). Možemo gledati limes [spoiler][latex]\displaystyle \lim_{(x, 0) \to (0, 0)} \frac{2 x + y}{x^2 - 4 y^2}[/latex][/spoiler]
2.b Definirajmo fje [latex]f, g : \mathbb{R}^2 \to \mathbb{R}[/latex] sa [latex]f(x, y) = 2 x - y[/latex] i [latex]g(x, y) = x^2 + 2 y^2[/latex]. Primjetimo da je zadani skup jednak [latex]f^{-1}(\langle -\infty, 0 \rangle \cup \langle 0, +\infty \rangle) \cap g^{-1}(\langle 1, +\infty \rangle)[/latex]. Sad iskoristimo otvorenost skupova [latex]\langle -\infty, 0 \rangle \cup \langle 0, +\infty \rangle[/latex] i [latex]\langle 1, +\infty \rangle[/latex], neprekidnost fja f i g te jedno svojstvo otvorenih skupova (presjek dva otvorena skupa je otvoren). Time je dokaz gotov.
1.b Kritično mjesto je 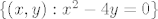 (a.k.a. parabola). U ostalim točkama je fja definirana, neprekidna, dakle bla, bla, bla... (a.k.a. parabola). U ostalim točkama je fja definirana, neprekidna, dakle bla, bla, bla...
Primjetimo da je 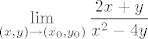 (za (za 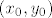 td. td. 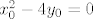 ) oblika ) oblika 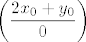 . To znači da taj limes divergira ako je . To znači da taj limes divergira ako je 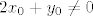 . Tako nam se interesantan skup smanjuje na dvije točke: . Tako nam se interesantan skup smanjuje na dvije točke: 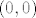 i i 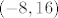 (rješenja sustava (rješenja sustava 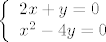 ). Može se pokazati da fja nema limes niti u jednoj od tih točaka. ). Može se pokazati da fja nema limes niti u jednoj od tih točaka.
Za točku (0,0) možemo promotriti kad | Spoiler [hidden; click to show]: | |
a za (-8,16) | Spoiler [hidden; click to show]: | 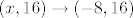 i 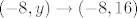 |
1.c Na vrlo sličan način kao gore dođemo do točke (0,0). Možemo gledati limes | Spoiler [hidden; click to show]: | |
2.b Definirajmo fje 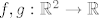 sa sa 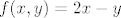 i i 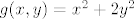 . Primjetimo da je zadani skup jednak . Primjetimo da je zadani skup jednak 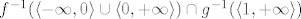 . Sad iskoristimo otvorenost skupova . Sad iskoristimo otvorenost skupova 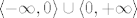 i i 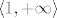 , neprekidnost fja f i g te jedno svojstvo otvorenih skupova (presjek dva otvorena skupa je otvoren). Time je dokaz gotov. , neprekidnost fja f i g te jedno svojstvo otvorenih skupova (presjek dva otvorena skupa je otvoren). Time je dokaz gotov.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:58 pet, 22. 10. 2010 Naslov: Postano: 17:58 pet, 22. 10. 2010 Naslov: |
    |
|
|
[quote="Anonymous"]E a zas ja nemogu otvorit ove kodove(kod limesa) koje si posto ?[/quote]
Ne znam. Ja samo kliknem na taj prozorčič i otvori se. Ako nikak ne ide, stavi kursor na zelenog smajlića gore desno, pa traži [ spoiler ][ /spoiler ] blokove.
2.a Praslika zatvorenog skupa po neprekidnoj fji je zatvoren u domeni. To znači da je [latex]f^{-1}([0, 1])[/latex] zatvoren u [latex]\overline{K}(0, 1)[/latex]. "Zatvoren u [latex]\overline{K}(0, 1)[/latex]" znači da postoji zatvoreni skup [latex]Z \subseteq \mathbb{R}^2[/latex] td. [latex]\overline{K}(0, 1) \cap Z = f^{-1}([0, 1])[/latex]. No, presjek dva zatvorena skup je zatvoren, pa je [latex]f^{-1}([0, 1])[/latex] zatvoren (u [latex]\mathbb{R}^2[/latex]). Očito je [latex]f^{-1}([0, 1]) \subseteq \overline{K}(0, 1)[/latex], što znači da je [latex]f^{-1}([0, 1])[/latex] omeđen. Napokon, kako samo pokazali da je [latex]f^{-1}([0, 1])[/latex] zatvoren i omeđen, slijedi da je kompaktan.
1.a Kao u b i c djelu, dođemo do točke (0,0). Možemo gledati limes kad [latex](x, 0) \to (0, 0)[/latex]. Dobimo da tada divergira, pa nema limesa u (0, 0).
| Anonymous (napisa): | | E a zas ja nemogu otvorit ove kodove(kod limesa) koje si posto ? |
Ne znam. Ja samo kliknem na taj prozorčič i otvori se. Ako nikak ne ide, stavi kursor na zelenog smajlića gore desno, pa traži [ spoiler ][ /spoiler ] blokove.
2.a Praslika zatvorenog skupa po neprekidnoj fji je zatvoren u domeni. To znači da je 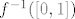 zatvoren u zatvoren u 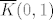 . "Zatvoren u . "Zatvoren u 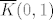 " znači da postoji zatvoreni skup " znači da postoji zatvoreni skup  td. td. 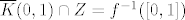 . No, presjek dva zatvorena skup je zatvoren, pa je . No, presjek dva zatvorena skup je zatvoren, pa je 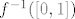 zatvoren (u zatvoren (u 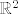 ). Očito je ). Očito je 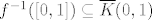 , što znači da je , što znači da je 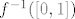 omeđen. Napokon, kako samo pokazali da je omeđen. Napokon, kako samo pokazali da je 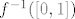 zatvoren i omeđen, slijedi da je kompaktan. zatvoren i omeđen, slijedi da je kompaktan.
1.a Kao u b i c djelu, dođemo do točke (0,0). Možemo gledati limes kad 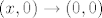 . Dobimo da tada divergira, pa nema limesa u (0, 0). . Dobimo da tada divergira, pa nema limesa u (0, 0).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:37 pet, 22. 10. 2010 Naslov: Postano: 20:37 pet, 22. 10. 2010 Naslov: |
    |
|
|
Čini mi se kao da želiš pokazati da je D kompaktan (što očito nije, jer nije zatvoren), pa se onda vraćaš na f(D). :/
A opet, izgleda da si uspjela odrediti da je f(D) = [0, 1], što je očito kompaktno. :D
I pazi: [latex]f^{-1}([0, 1]) = \mathbb{R} \times [-1, 1][/latex]. ;)
Čini mi se kao da želiš pokazati da je D kompaktan (što očito nije, jer nije zatvoren), pa se onda vraćaš na f(D). 
A opet, izgleda da si uspjela odrediti da je f(D) = [0, 1], što je očito kompaktno. 
I pazi:  . . 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:55 pet, 22. 10. 2010 Naslov: Postano: 20:55 pet, 22. 10. 2010 Naslov: |
    |
|
|
Sorry, malo sam se zanio (gledao sam kao da je domena cijeli [latex]\mathbb{R}^2[/latex] (da, -1 mora biti u tom slučaju ;))). U pravu si da je [latex]D = f^{-1}([0, 1])[/latex], pa je onda D zatvoren u D. Poanta je što to ne implicira da je D zatvoren (u [latex]\mathbb{R}^2[/latex]), pa iz toga ne možeš zaključiti da je kompaktan, a i time da je i f(D) kompaktan. :)
Sorry, malo sam se zanio (gledao sam kao da je domena cijeli 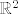 (da, -1 mora biti u tom slučaju (da, -1 mora biti u tom slučaju  )). U pravu si da je )). U pravu si da je 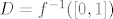 , pa je onda D zatvoren u D. Poanta je što to ne implicira da je D zatvoren (u , pa je onda D zatvoren u D. Poanta je što to ne implicira da je D zatvoren (u 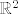 ), pa iz toga ne možeš zaključiti da je kompaktan, a i time da je i f(D) kompaktan. ), pa iz toga ne možeš zaključiti da je kompaktan, a i time da je i f(D) kompaktan. 
|
|
| [Vrh] |
|
|











