|
Ovaj drugi je malo brzi pa to odmah:
Pretpostavimo da je g strogo padajuca.
Buduci je f surjekcija, postoje a, b takvi da je f(a)=0 i f(b)=-1
Zbog toga dobivamo g(a)=g(b)=0, a to je kontradikcija s pretpostavkom da g strogo pada (ako strogo pada, onda je, posebno, injektivna)
Prvi:
Pretpostavimo da postoji takva funkcija f.
Tada ona mora zadovoljavati nekakve uvjete, do kojih sada pokusavamo doci:
[latex]g(x)=(2^{f(x)})^2-2^{f(x)}[/latex], dakle g je kompozicija ovih triju funkcija:
[latex]f_1(x)=f(x)[/latex]
[latex]f_2(x)=2^x[/latex]
[latex]f_3(x)=x^2-x[/latex]
[latex]f[/latex] je padajuca, [latex]f_2[/latex] strogo rastuca, pa znamo da je[latex] f_2 \circ f[/latex] padajuca funkcija cija je kodomena podskup od [latex]<0,\infty>[/latex]. Takodjer, za f je nuzan uvjet da bude strogo padajuca, jer inace nije injektivna (pa bi postojale dvije vrijednosti u kojima je g jednaka)
E sad, da bi g bila strogo rastuca, dovoljno je osigurati da [latex]f_3 [/latex] djeluje na intervalu [latex]<0,\frac{1}{2}][/latex] jer je tamo padajuca (pa bi g bila strogo rastuca, kao kompozicija s. pad, s. rast, s. pad).
Dakle, morali bismo naci funkciju f koja je strogo padajuca, i takva da je slika od [latex]2^f[/latex] u intervalu [latex]<0,\frac{1}{2}][/latex].
Iz ovog zakljucujemo da slika od f treba biti podskup od <-\infty, -1>
(jer [latex]2^x \in <0,\frac{1}{2}][/latex] kad je x iz tog intervala)
Sad si malo nacrtamo, pogledamo i skuzimo da ce nam bit dobra neka lijepa funkcija tipa [latex]f(x)=-1-2^x[/latex]. Naravno, to bi jos trebalo provjerit i sve, al sto se tice trazenja funkcije, ovo je otprilike kako bi moglo ic...
Ovaj drugi je malo brzi pa to odmah:
Pretpostavimo da je g strogo padajuca.
Buduci je f surjekcija, postoje a, b takvi da je f(a)=0 i f(b)=-1
Zbog toga dobivamo g(a)=g(b)=0, a to je kontradikcija s pretpostavkom da g strogo pada (ako strogo pada, onda je, posebno, injektivna)
Prvi:
Pretpostavimo da postoji takva funkcija f.
Tada ona mora zadovoljavati nekakve uvjete, do kojih sada pokusavamo doci:
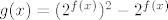 , dakle g je kompozicija ovih triju funkcija: , dakle g je kompozicija ovih triju funkcija:
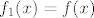
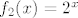
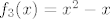
 je padajuca, je padajuca, 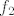 strogo rastuca, pa znamo da je strogo rastuca, pa znamo da je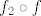 padajuca funkcija cija je kodomena podskup od padajuca funkcija cija je kodomena podskup od 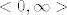 . Takodjer, za f je nuzan uvjet da bude strogo padajuca, jer inace nije injektivna (pa bi postojale dvije vrijednosti u kojima je g jednaka) . Takodjer, za f je nuzan uvjet da bude strogo padajuca, jer inace nije injektivna (pa bi postojale dvije vrijednosti u kojima je g jednaka)
E sad, da bi g bila strogo rastuca, dovoljno je osigurati da 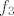 djeluje na intervalu djeluje na intervalu 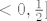 jer je tamo padajuca (pa bi g bila strogo rastuca, kao kompozicija s. pad, s. rast, s. pad). jer je tamo padajuca (pa bi g bila strogo rastuca, kao kompozicija s. pad, s. rast, s. pad).
Dakle, morali bismo naci funkciju f koja je strogo padajuca, i takva da je slika od 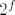 u intervalu u intervalu 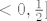 . .
Iz ovog zakljucujemo da slika od f treba biti podskup od ←\infty, -1>
(jer 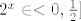 kad je x iz tog intervala) kad je x iz tog intervala)
Sad si malo nacrtamo, pogledamo i skuzimo da ce nam bit dobra neka lijepa funkcija tipa  . Naravno, to bi jos trebalo provjerit i sve, al sto se tice trazenja funkcije, ovo je otprilike kako bi moglo ic... . Naravno, to bi jos trebalo provjerit i sve, al sto se tice trazenja funkcije, ovo je otprilike kako bi moglo ic...
|






