| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:20 ned, 24. 10. 2010 Naslov: Postano: 17:20 ned, 24. 10. 2010 Naslov: |
    |
|
|
Ako bi preko definicije dokazivali, za točku [latex](x_0, y_0) \in \mathbb{R}^2 \setminus {(0, 0)}[/latex] uzmemo radijus [latex]\| (x_0, y_0) \|[/latex].
Treba pokazati [latex]K((x_0, y_0), \| (x_0, y_0)\|) \subseteq \mathbb{R}^2 \setminus \{(0, 0)\}[/latex]. Uzmimo proizvoljan [latex](x, y) \in K((x_0, y_0), \| (x_0, y_0)\|)[/latex]. Vrijedi
[latex]$\begin{align*}\| (x_0, y_0) \| = \| (x_0, y_0) - (x, y) + (x, y) \| \leq \underbrace{\| (x_0, y_0) - (x, y) \|}_{= d((x_0, y_0), (x, y))} + \| (x, y) \| < \| (x_0, y_0) \| + \| (x, y) \|\end{align*}$[/latex]
Pokratimo [latex]\| (x_0, y_0) \|[/latex] i dobimo [latex]\| (x, y) \| > 0[/latex]. To povlači [latex](x, y) \neq (0, 0)[/latex], pa je [latex](x, y) \in \mathbb{R}^2 \setminus \{(0, 0)\}[/latex].
Ako bi preko definicije dokazivali, za točku  uzmemo radijus uzmemo radijus 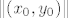 . .
Treba pokazati 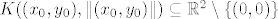 . Uzmimo proizvoljan . Uzmimo proizvoljan 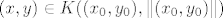 . Vrijedi . Vrijedi
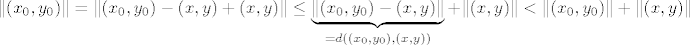
Pokratimo 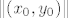 i dobimo i dobimo 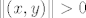 . To povlači . To povlači 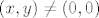 , pa je , pa je 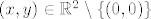 . .
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:10 ned, 24. 10. 2010 Naslov: Postano: 19:10 ned, 24. 10. 2010 Naslov: |
    |
|
|
2. Dokazati to preko neprekidne fje je trivijalno, što se ne može reći za dokazivanje preko definicije.
Uzmimo proizvoljnu točku [latex]T_0 = (x_0, y_0)[/latex] iz S i proizvoljnu točku [latex]T = (x, y) \in K(T_0, r)[/latex] (r ćemo kasnije definirati). Trebalo bi pokazati [latex]x y < 1[/latex]. Glavna fora je uočiti [latex]x y = (x - x_0)(y - y_0) + x y_0 + x_0 y - x_0 y_0 = (x - x_0)(y - y_0) + (x - x_0) y_0 + x_0 (y - y_0) + x_0 y_0[/latex]. Kad iskoristimo [latex]T \in K(T_0, r)[/latex], dobimo [latex]x y < r^2 + r y_0 + x_0 r + x_0 y_0[/latex]. Znači, trebamo odabrati takav r da je [latex]r^2 + r y_0 + x_0 r + x_0 y_0 \leq 1[/latex]. Nultočke su [latex]\displaystyle r_{1, 2} = \frac{-(x_0 + y_0) \pm \sqrt{(x_0 + y_0)^2 + 4 (1 - x_0 y_0)}}{2}[/latex]. Sjetimo se da je [latex]x_0 y_0 < 1[/latex], pa je očito [latex]\displaystyle \frac{-(x_0 + y_0) + \sqrt{(x_0 + y_0)^2 + 4 (1 - x_0 y_0)}}{2}[/latex] pozitivno. Uzmimo stoga da je r baš jednak tom broju, i to je to.
6. Interior mu je prazan skup, jer nema unutarnjih točaka. Zatvarač je on sam, jer je zatvoren. Njegov rub je također on sam (očito je [latex]\overline{\mathbb{R}^n \setminus S} = \mathbb{R}^n[/latex]).
8. [latex]\partial S = \overline{S} \cap \overline{\mathbb{R} \setminus S} = (S \cup \{ 0 \}) \cap \mathbb{R} = S \cup \{ 0 \}[/latex]
Drugi način određivanja ruba je preko zatvarača i interiora. Može se pokazati da je [latex]\overline{S} = {\sf Int} \, S \cup \partial S[/latex] (za bilo koji skup S), i da su pritom interior i rub disjunktni. Slijedi da je [latex]\partial S = \overline{S} \setminus {\sf Int} \, S[/latex].
[quote="šišmiš"]kako da pametno odredujem skopove gomilista - to me ponekad buni ??[/quote]
Po osjećaju, gledaš što je jako blizu (na udaljenosti 0) tvom skupu, ali paziš na izolirane točke. Da budeš siguran, prvojeriš po definiciji (odabireš sve manje i manje kugle). Na kraju, ako treba, dokažeš.
Imaš li možda neki konkretan primjer koji te muči?
2. Dokazati to preko neprekidne fje je trivijalno, što se ne može reći za dokazivanje preko definicije.
Uzmimo proizvoljnu točku 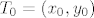 iz S i proizvoljnu točku iz S i proizvoljnu točku 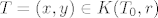 (r ćemo kasnije definirati). Trebalo bi pokazati (r ćemo kasnije definirati). Trebalo bi pokazati 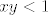 . Glavna fora je uočiti . Glavna fora je uočiti 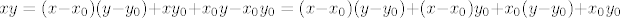 . Kad iskoristimo . Kad iskoristimo 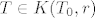 , dobimo , dobimo 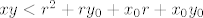 . Znači, trebamo odabrati takav r da je . Znači, trebamo odabrati takav r da je 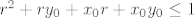 . Nultočke su . Nultočke su 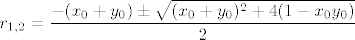 . Sjetimo se da je . Sjetimo se da je 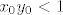 , pa je očito , pa je očito 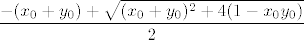 pozitivno. Uzmimo stoga da je r baš jednak tom broju, i to je to. pozitivno. Uzmimo stoga da je r baš jednak tom broju, i to je to.
6. Interior mu je prazan skup, jer nema unutarnjih točaka. Zatvarač je on sam, jer je zatvoren. Njegov rub je također on sam (očito je 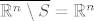 ). ).
8. 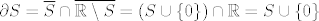
Drugi način određivanja ruba je preko zatvarača i interiora. Može se pokazati da je 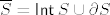 (za bilo koji skup S), i da su pritom interior i rub disjunktni. Slijedi da je (za bilo koji skup S), i da su pritom interior i rub disjunktni. Slijedi da je 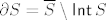 . .
| šišmiš (napisa): | | kako da pametno odredujem skopove gomilista - to me ponekad buni ?? |
Po osjećaju, gledaš što je jako blizu (na udaljenosti 0) tvom skupu, ali paziš na izolirane točke. Da budeš siguran, prvojeriš po definiciji (odabireš sve manje i manje kugle). Na kraju, ako treba, dokažeš.
Imaš li možda neki konkretan primjer koji te muči?
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:03 ned, 24. 10. 2010 Naslov: Postano: 21:03 ned, 24. 10. 2010 Naslov: |
    |
|
|
a) [latex][0, 1][/latex]
b) Valjda se misli na [latex]\{ (x, y) \in \mathbb{R}^2 : x \in \langle 0, 1 \rangle \cup \{ 2 \} \} = (\langle 0, 1 \rangle \cup \{ 2 \}) \times \mathbb{R}[/latex]. Skup gomilišta je [latex]([0, 1] \cup \{ 2 \}) \times \mathbb{R}[/latex].
c) Opet, trebalo bi biti [latex](x, y) \in \mathbb{R}^2[/latex] umjesto [latex]x \in \mathbb{R}^2[/latex]. Taj skup je jednak [latex](\langle 0, 1 \rangle \cup \{ 2 \}) \times \{ 0 \}[/latex]. Skup gomilišta je [latex][0, 1] \times \{ 0 \}[/latex].
d) Dvojka samo zbunjuje. Možemo je slobodno maknuti jer je [latex]f : \mathbb{Q} \to \mathbb{Q}[/latex], [latex]f(q) = 2q[/latex] bijekcija (ima očiti inverz). Dakle, zadani skup jednak je [latex]\mathbb{Q} \times \{ \frac{1}{m} : m \in \mathbb{Z} \setminus \{0\} \}[/latex]. Kad si to nacrtamo (u glavi), vidimo da je to skup pravaca [latex]y = \frac{1}{m}[/latex] bez točaka koje imaju iracionalne x-koordinate. Iz toga naslućujemo da je skup gomilišta [latex]\mathbb{R} \times (\{ \frac{1}{m} : m \in \mathbb{Z} \setminus \{ 0 \} \} \cup \{0\} )[/latex].
Fora je da si vizualiziraš taj skup. Onda je lakše odrediti što bi bio skup gomilišta. Problem nastaje kad ima više od 3 dimenzija.
Sve ovo se može dokazati po definiciji razbijanjem na slučajeve.
a) 
b) Valjda se misli na 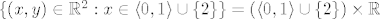 . Skup gomilišta je . Skup gomilišta je 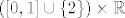 . .
c) Opet, trebalo bi biti 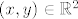 umjesto umjesto  . Taj skup je jednak . Taj skup je jednak 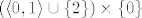 . Skup gomilišta je . Skup gomilišta je 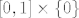 . .
d) Dvojka samo zbunjuje. Možemo je slobodno maknuti jer je 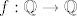 , , 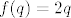 bijekcija (ima očiti inverz). Dakle, zadani skup jednak je bijekcija (ima očiti inverz). Dakle, zadani skup jednak je 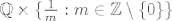 . Kad si to nacrtamo (u glavi), vidimo da je to skup pravaca . Kad si to nacrtamo (u glavi), vidimo da je to skup pravaca 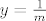 bez točaka koje imaju iracionalne x-koordinate. Iz toga naslućujemo da je skup gomilišta bez točaka koje imaju iracionalne x-koordinate. Iz toga naslućujemo da je skup gomilišta 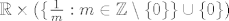 . .
Fora je da si vizualiziraš taj skup. Onda je lakše odrediti što bi bio skup gomilišta. Problem nastaje kad ima više od 3 dimenzija.
Sve ovo se može dokazati po definiciji razbijanjem na slučajeve.
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:07 ned, 24. 10. 2010 Naslov: Postano: 22:07 ned, 24. 10. 2010 Naslov: |
    |
|
|
[quote="Black Mamba"]Kako formalno pokažem 5.zadatak?
Ili neki od 11.?
Hvala :)[/quote]
Peti najelegantnije možeš preko neprekidne fje [latex]f = \| \cdot \|[/latex]. Očito je [latex]S = f^{-1}(\{1\})[/latex]. Za [latex]\{1\}[/latex] nije teško vidjeti iz definicije da je zatvoren.
Mislim da je 11. najbolje preko definicije.
[quote="šišmiš"]jel ti de da pogledat sada drugu zadacu:neke od ovih zadataka :
zad 4, 5,6 8,10,11[/quote]
4. [latex]\mathbb{N}[/latex]
5. [latex]\langle 0, 1 \rangle[/latex]
6. [latex]\mathbb{N} \times \{ \frac{1}{n} : n \in \mathbb{N} \}[/latex]
8. [latex]\{ K(1, r) : r \in \langle 0, 1 \rangle \}[/latex]
10. Ograničen je. Preostaje pokazati zatvorenost. Možemo preko definicije. Neka je [latex]x \in \mathbb{R}^n \setminus (\{a_1, a_2, \ldots\} \cup \{a\}) =: A^C[/latex] proizvoljan. Trebamo naći [latex]r > 0[/latex] td. [latex]K(x, r) \subseteq A^C[/latex]. Pretpostavimo da ne postoji takav r, tj. da za svaki [latex]r > 0[/latex] postoji [latex]x_r \in K(x, r) \cap A[/latex]. Možemo formirati podniz [latex](a_{p(k)})_k[/latex] od [latex](a_k)_k[/latex] td. [latex]a_{p(k)} \in K(x, \frac{1}{k})[/latex]. Po tm. o sendviču slijedi da [latex](a_{p(k)})_k[/latex] konvergira u x. No [latex](a_{p(k)})_k[/latex] konvergira i u a kao podniz konvergentnog niza. Zbog jedinstvenosti limesa slijedi [latex]x = a[/latex], što je u kontradikciji s načinom na koji smo odabrali x. Slijedi da je A zatvoren, a kako je i ograničen, slijedi da je kompaktan.
11. Da, jer je ograničen.
| Black Mamba (napisa): | Kako formalno pokažem 5.zadatak?
Ili neki od 11.?
Hvala  |
Peti najelegantnije možeš preko neprekidne fje 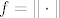 . Očito je . Očito je 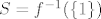 . Za . Za 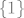 nije teško vidjeti iz definicije da je zatvoren. nije teško vidjeti iz definicije da je zatvoren.
Mislim da je 11. najbolje preko definicije.
| šišmiš (napisa): | jel ti de da pogledat sada drugu zadacu:neke od ovih zadataka :
zad 4, 5,6 8,10,11 |
4. 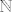
5. 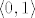
6. 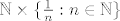
8. 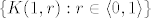
10. Ograničen je. Preostaje pokazati zatvorenost. Možemo preko definicije. Neka je 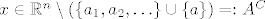 proizvoljan. Trebamo naći proizvoljan. Trebamo naći 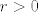 td. td. 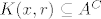 . Pretpostavimo da ne postoji takav r, tj. da za svaki . Pretpostavimo da ne postoji takav r, tj. da za svaki 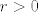 postoji postoji 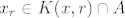 . Možemo formirati podniz . Možemo formirati podniz 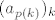 od od 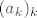 td. td. 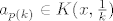 . Po tm. o sendviču slijedi da . Po tm. o sendviču slijedi da 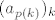 konvergira u x. No konvergira u x. No 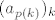 konvergira i u a kao podniz konvergentnog niza. Zbog jedinstvenosti limesa slijedi konvergira i u a kao podniz konvergentnog niza. Zbog jedinstvenosti limesa slijedi  , što je u kontradikciji s načinom na koji smo odabrali x. Slijedi da je A zatvoren, a kako je i ograničen, slijedi da je kompaktan. , što je u kontradikciji s načinom na koji smo odabrali x. Slijedi da je A zatvoren, a kako je i ograničen, slijedi da je kompaktan.
11. Da, jer je ograničen.
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 19:22 uto, 23. 11. 2010 Naslov: Postano: 19:22 uto, 23. 11. 2010 Naslov: |
    |
|
|
može mala pomoć kod 3.zadatka iz http://web.math.hr/nastava/difraf/dif/2007-08/zadaca_df.pdf?
naime,izračunala sam parcijalne derivacije kada je (x,y)=(0,0) i kada nije.
u prvom sam slučaju dobila da je parc.der po x u (0,0) = 1
po y =-1
u drugom slučaju u proizvoljnoj točki (x,y) po x = (x^4 + 3x^2y^2 + 2y^3x)/(x^2+y^2)^2
po y= (-y^4 - 3x^2y^2 - 2x^3y)/(x^2+y^2)^2
i sada neznam kako znam je li f-ja derivabilna u (0,0)? trebam li u ovom drugom slučaju uvrstiti (0,0) umjesto x(ali mi onda ispadne 0/0), ili računati limes,ako da, koji i kako?
može mala pomoć kod 3.zadatka iz http://web.math.hr/nastava/difraf/dif/2007-08/zadaca_df.pdf?
naime,izračunala sam parcijalne derivacije kada je (x,y)=(0,0) i kada nije.
u prvom sam slučaju dobila da je parc.der po x u (0,0) = 1
po y =-1
u drugom slučaju u proizvoljnoj točki (x,y) po x = (x^4 + 3x^2y^2 + 2y^3x)/(x^2+y^2)^2
po y= (-y^4 - 3x^2y^2 - 2x^3y)/(x^2+y^2)^2
i sada neznam kako znam je li f-ja derivabilna u (0,0)? trebam li u ovom drugom slučaju uvrstiti (0,0) umjesto x(ali mi onda ispadne 0/0), ili računati limes,ako da, koji i kako?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 20:37 čet, 9. 12. 2010 Naslov: Postano: 20:37 čet, 9. 12. 2010 Naslov: |
    |
|
|
imamo [latex]f:(\mathbb{R}^n)^2 \rightarrow \mathbb{R}^n.[/latex]
Al kak uvijek promatramo funkcije [latex]R^n -> R^m[/latex], onda je ok poistovjetiti [latex](R^n)^2[/latex] s [latex]R^{2n}[/latex]
Pritom x mozemo promatrati kao projekciju vektora (x,y) (ovaj sada ima 2n komponenata) na prvih n komponenata, a y na drugih n. Obje te projekcije su linearni operatori. Dalje se moze nastaviti kao i inace, dakle sada imamo funkciju [latex]f(x,y)=<a,p_1(x,y)>p_2(x,y) + cos(<p_1(x,y),p_1(x,y)>)b[/latex], gdje su [latex]p_1[/latex] i [latex]p_2[/latex] spomenute projekcije (njihovi diferencijali su upravo one same). (pritom ovdje pise f(x,y) samo da bismo lakse razlikovali dva dijela istog vektora)
Sad se to dalje moze raditi kao i svi ostali zadaci, uz koristenje onih standardnih svojstava, npr. pravila za kompoziciju, produkt, ...
mislim da se na kraju dobije nesto kao [latex]Df(x,y)(h_x,h_y)=<a,h_x>y+<a,x>h_y-2sin<x,x><x,h_x>[/latex]
EDIT: ups, izgleda da sam malo nepazljivo citao zadatak pa mi je promaknuo R^3 :D
U svakom slucaju, hvala kolegi flameu na ispravku (ispod).
P.S: isprike na nekoristenju neprofesionalnih spicastih zagrada :)
imamo 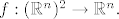
Al kak uvijek promatramo funkcije 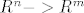 , onda je ok poistovjetiti , onda je ok poistovjetiti 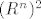 s s 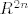
Pritom x mozemo promatrati kao projekciju vektora (x,y) (ovaj sada ima 2n komponenata) na prvih n komponenata, a y na drugih n. Obje te projekcije su linearni operatori. Dalje se moze nastaviti kao i inace, dakle sada imamo funkciju 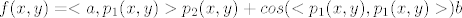 , gdje su , gdje su 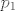 i i 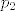 spomenute projekcije (njihovi diferencijali su upravo one same). (pritom ovdje pise f(x,y) samo da bismo lakse razlikovali dva dijela istog vektora) spomenute projekcije (njihovi diferencijali su upravo one same). (pritom ovdje pise f(x,y) samo da bismo lakse razlikovali dva dijela istog vektora)
Sad se to dalje moze raditi kao i svi ostali zadaci, uz koristenje onih standardnih svojstava, npr. pravila za kompoziciju, produkt, ...
mislim da se na kraju dobije nesto kao 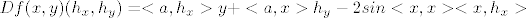
EDIT: ups, izgleda da sam malo nepazljivo citao zadatak pa mi je promaknuo R^3 
U svakom slucaju, hvala kolegi flameu na ispravku (ispod).
P.S: isprike na nekoristenju neprofesionalnih spicastih zagrada 
Zadnja promjena: pbakic; 20:00 pet, 10. 12. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 15:31 pet, 10. 12. 2010 Naslov: Postano: 15:31 pet, 10. 12. 2010 Naslov: |
    |
|
|
U principu, ono sto je kolega pbakic napisao je tocno, jedino sto je kolega previdio da u ovom konkretnom slucaju varijable x i y nisu iz jednakodimenzionalnih prostora.
Ovo bi bila nekakva ideja rjesavanja pomocu parcijalnih derivacija (kazem ideja jer nisam provjeravao da li je rjesenje ispravno :P )
[latex]a \in \mathbb{R}^n \implies x \in \mathbb{R}^n, b\in \mathbb{R}^3 \implies y \in \mathbb{R}^3[/latex]
Funkciju sad mozemo shvatiti ovako:
[latex]
f(x, y_1, y_2, y_3) = (y_1 \langle a, x \rangle + b_1 \cos\|x\|^2, y_2 \langle a, x \rangle + b_2 \cos\|x\|^2, y_3 \langle a, x \rangle + b_3 \cos\|x\|^2) \\
\implies \\
\partial_{x_i} f_j (x,y) = y_j a_i - 2b_j \sin \|x\|^2 x_i \\
\partial_{y_i} f_j (x,y) = \langle a, x \rangle[/latex]
za [latex]i = j[/latex], a inace [latex]0[/latex]
Sad imamo Jacobijevu matricu:
[latex]\triangledown f(x,y) = \left(
\begin{array}{ccc}
y_1a_1 -2b_1\sin\|x\|^2 x_1&\ldots&y_1a_n-2b_1\sin\|x\|^2x_n&\langle a,x\rangle &0&0\\
y_2 a_1 - 2b_2 \sin \|x\|^2 x_1 & \ldots & y_2 a_n - 2b_2\sin \|x\|^2 x_n & 0 & \langle a, x \rangle & 0\\
y_2 a_1 - 2b_2 \sin \|x\|^2 x_1 & \ldots & y_2 a_n - 2b_2\sin \|x\|^2 x_n & 0 & 0 & \langle a, x \rangle \end{array}
\right)[/latex]
(iz nekog razloga je ne zeli alignati kako bi trebalo, matrica bi trebala biti dimenzija 3 x (n+3))
pa imamo:
[latex]D f(x,y) (x_0,y_0) = \triangledown f(x,y) \cdot \left(\begin{array}{ccc} x_0^1 \\ \cdot \\ \cdot \\ \cdot \\x_0^n \\ y_0^1 \\ y_0^2 \\ y_0^3 \end{array}\right)[/latex]
odnosno, nako sredjivanja:
[latex]D f(x,y) (x_0,y_0) = \langle a, x_0 \rangle \cdot y - 2\langle x, x_0\rangle \sin\|x\|^2 \cdot b + \langle a,x \rangle \cdot y_0[/latex]
Napomena: Funkciju smo po potrebi shvacali kao preslikavanje [latex]\mathbb{R}^n \times \mathbb{R}^3 \rightarrow \mathbb{R}^3, \mathbb{R}^n \times \mathbb{R} \times \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}^3, \mathbb{R} \times \mathbb{R} \times \cdots \times \mathbb{R} \rightarrow \mathbb{R}^3[/latex]. To smijemo jer su ti prostori ne samo izomorfni, vec medju njima postoji prirodan izomorfizam.
U principu, ono sto je kolega pbakic napisao je tocno, jedino sto je kolega previdio da u ovom konkretnom slucaju varijable x i y nisu iz jednakodimenzionalnih prostora.
Ovo bi bila nekakva ideja rjesavanja pomocu parcijalnih derivacija (kazem ideja jer nisam provjeravao da li je rjesenje ispravno  ) )
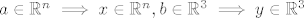
Funkciju sad mozemo shvatiti ovako:
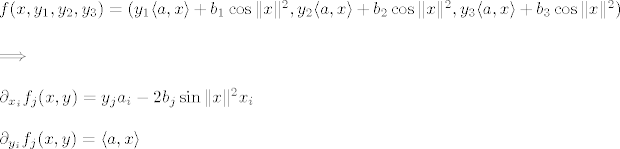
za 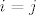 , a inace , a inace 
Sad imamo Jacobijevu matricu:
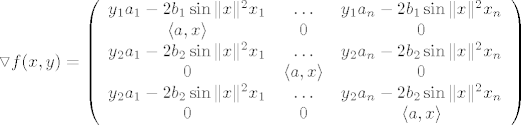
(iz nekog razloga je ne zeli alignati kako bi trebalo, matrica bi trebala biti dimenzija 3 x (n+3))
pa imamo:
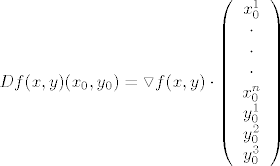
odnosno, nako sredjivanja:
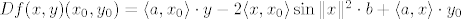
Napomena: Funkciju smo po potrebi shvacali kao preslikavanje 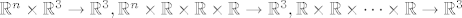 . To smijemo jer su ti prostori ne samo izomorfni, vec medju njima postoji prirodan izomorfizam. . To smijemo jer su ti prostori ne samo izomorfni, vec medju njima postoji prirodan izomorfizam.
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|














