|
[quote="Anonymous"]http://web.math.unizg.hr/nastava/ma34/ma3/2005-06/kol1.pdf
Jel bi mogul nekton rijesit prvi I drugi zadatak[/quote]
Postoje službena rješenja: [url=http://web.math.hr/nastava/ma34/kolokviji_ma3.html]link[/url].
[quote="Anonymous"]http://web.math.hr/nastava/ma34/ma3/2006-07/kol1.pdf
I prvi odavde[/quote]
Može se naslutiti da je fja nepr. u [latex](\sqrt{2}, \sqrt{2})[/latex], jer je funkcijska vrijednost jednaka [latex]\sqrt{2}[/latex], a [latex]f|_{\{ (x, y) : x^2 \in \mathbb{Q} \, \& \, y^2 \in \mathbb{Q} \}}[/latex] i [latex]f|_{\{ (x, y) : x^2 \notin \mathbb{Q} \, \vee \, y^2 \notin \mathbb{Q} \}}[/latex] su "oko" [latex](\sqrt{2}, \sqrt{2})[/latex] "blizu" [latex]\sqrt{2}[/latex].
Krenimo na dokaz. Neka je [latex]\varepsilon > 0[/latex] proizvoljan. Treba naći takav [latex]\delta > 0[/latex] da [latex]d((x, y), (\sqrt{2}, \sqrt{2})) < \delta[/latex] (iz toga slijedi [latex]|x - \sqrt{2}| < \delta[/latex] i [latex]|y - \sqrt{2}| < \delta[/latex], jer vrijedi [latex]|x - \sqrt{2}| \leq d((x, y), (\sqrt{2}, \sqrt{2}))[/latex] i [latex]|y - \sqrt{2}| \leq d((x, y), (\sqrt{2}, \sqrt{2}))[/latex]) povlači [latex]|f(x, y) - \sqrt{2}| < \varepsilon[/latex]. Promotrimo posebno dva slučaja:
1° [latex]x^2 \in \mathbb{Q}[/latex] i [latex]y^2 \in \mathbb{Q}[/latex]. Tada je [latex]|f(x, y) - \sqrt{2}| = |x - \sqrt{2}| < \varepsilon[/latex]. Iz toga vidimo da možemo uzeti [latex]\delta = \varepsilon[/latex].
2° [latex]x^2 \notin \mathbb{Q}[/latex] ili [latex]y^2 \notin \mathbb{Q}[/latex]. Isto kao u 1°, samo se na jednom mjestu x zamjeni s y.
| Anonymous (napisa): | http://web.math.unizg.hr/nastava/ma34/ma3/2005-06/kol1.pdf
Jel bi mogul nekton rijesit prvi I drugi zadatak |
Postoje službena rješenja: link.
| Anonymous (napisa): | http://web.math.hr/nastava/ma34/ma3/2006-07/kol1.pdf
I prvi odavde |
Može se naslutiti da je fja nepr. u 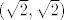 , jer je funkcijska vrijednost jednaka , jer je funkcijska vrijednost jednaka 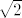 , a , a 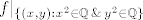 i i 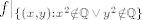 su "oko" su "oko" 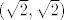 "blizu" "blizu" 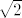 . .
Krenimo na dokaz. Neka je  proizvoljan. Treba naći takav proizvoljan. Treba naći takav 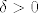 da da 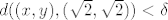 (iz toga slijedi (iz toga slijedi 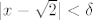 i i 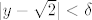 , jer vrijedi , jer vrijedi 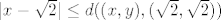 i i 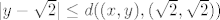 ) povlači ) povlači  . Promotrimo posebno dva slučaja: . Promotrimo posebno dva slučaja:
1° 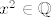 i i 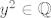 . Tada je . Tada je  . Iz toga vidimo da možemo uzeti . Iz toga vidimo da možemo uzeti 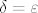 . .
2° 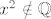 ili ili 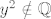 . Isto kao u 1°, samo se na jednom mjestu x zamjeni s y. . Isto kao u 1°, samo se na jednom mjestu x zamjeni s y.
|





