| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:23 sub, 23. 10. 2010 Naslov: Postano: 20:23 sub, 23. 10. 2010 Naslov: |
    |
|
|
[quote=".anchy."]f(x,y)=(x^2+y^2)sin(1/(xy))[/quote]
Kad tu napravimo supstituciju u polarne koordinate, dobivamo [latex]f(r, \theta) = r^2 \sin \dfrac{1}{r^2 \sin \theta \cos \theta}[/latex]. Vidimo da je [latex]-r^2 \leq f(r, \theta) \leq r^2[/latex], po teoremu o sendviču slijedi da je [latex]\displaystyle \lim_{r \to 0} f(r, \theta) = 0[/latex] (ne dira nas kaj se događa u tom sinusu).
Što se tiče osi x i y, promatrajmo točku [latex](x_0, 0)[/latex], [latex]x_0 \neq 0[/latex] (@pajopatak: primjeti da ta točka ne može biti u domeni :)). Odaberimo dva niza: [latex]\displaystyle \left( x_0, \frac{1}{x_0 n \pi} \right)[/latex], [latex]\displaystyle \left( x_0, \frac{1}{x_0 (\frac{\pi}{2} + 2 n \pi)} \right)[/latex]. Kod prvog je limes funkcijskih vrijednosti 0, a kod drugog [latex]x_0^2[/latex]. Dakle, ništa od limesa u [latex](x_0, 0)[/latex]. Analogno bi se moglo pokazati za y-os.
| .anchy. (napisa): | | f(x,y)=(x^2+y^2)sin(1/(xy)) |
Kad tu napravimo supstituciju u polarne koordinate, dobivamo 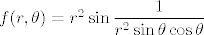 . Vidimo da je . Vidimo da je 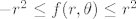 , po teoremu o sendviču slijedi da je , po teoremu o sendviču slijedi da je 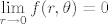 (ne dira nas kaj se događa u tom sinusu). (ne dira nas kaj se događa u tom sinusu).
Što se tiče osi x i y, promatrajmo točku 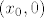 , , 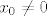 (@pajopatak: primjeti da ta točka ne može biti u domeni (@pajopatak: primjeti da ta točka ne može biti u domeni  ). Odaberimo dva niza: ). Odaberimo dva niza: 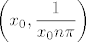 , , 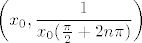 . Kod prvog je limes funkcijskih vrijednosti 0, a kod drugog . Kod prvog je limes funkcijskih vrijednosti 0, a kod drugog 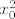 . Dakle, ništa od limesa u . Dakle, ništa od limesa u 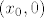 . Analogno bi se moglo pokazati za y-os. . Analogno bi se moglo pokazati za y-os.
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:45 ned, 24. 10. 2010 Naslov: Postano: 15:45 ned, 24. 10. 2010 Naslov: |
    |
|
|
@spot137: polarne + L'Hospital
@Genaro:
2009. 3. Promatraj ljepši oblik [latex]\displaystyle \frac{x^2}{y^2} \cdot \frac{\sin \frac{x^3 y^2}{x^2 + y^2}}{\frac{x^3 y^2}{x^2 + y^2}}[/latex]
5. Odgovor na svako pitanje je "i da i ne". Pod a) možeš uzeti [latex]A_1 = [0, 1][/latex] i [latex]A_2 = [2, 3][/latex], pa [latex]A_1 = [0, 1][/latex] i [latex]A_2 = \langle 1, 2][/latex]
Za b) nije teško izmisliti nešto, a c) je isto kao i b), jer je uvijek [latex]f(A_1 \cup A_2) = f(A_1) \cup f(A_2)[/latex].
2008. 3. Uzmi niz [latex](x, 0, z_0) \to (0, 0, z_0)[/latex].
@smajl: Neka je [latex](x, y) \in S[/latex] proizvoljan. Vrijedi [latex]d((0, 0), (x, y)) = \sqrt{x^2 + y^2} \leq \sqrt{4^2 + 1^2} \leq \sqrt{17}[/latex]. Dakle, [latex]S \subseteq \overline{K}(0, \sqrt{17})[/latex].
@spot137: polarne + L'Hospital
@Genaro:
2009. 3. Promatraj ljepši oblik 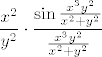
5. Odgovor na svako pitanje je "i da i ne". Pod a) možeš uzeti 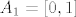 i i 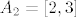 , pa , pa 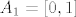 i i 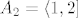
Za b) nije teško izmisliti nešto, a c) je isto kao i b), jer je uvijek 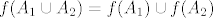 . .
2008. 3. Uzmi niz 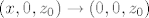 . .
@smajl: Neka je 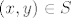 proizvoljan. Vrijedi proizvoljan. Vrijedi  . Dakle, . Dakle, 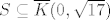 . .
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
 Postano: 22:05 ned, 24. 10. 2010 Naslov: Postano: 22:05 ned, 24. 10. 2010 Naslov: |
    |
|
|
f je ocito neprekidna u svim tockama (x,y) gdje je x^2+y^2 != 4
Zato je dovoljno provjeriti samo u tockama gdje je x^2+y^2=4
Tu se lako pokaze da f ima prekid u svakoj takvoj tocki, jer mozemo konstruirati dva niza, npr:
(xn,yn)=(x+1/n,y+1/n) => f(xn,yn)=2((x+1/n)^2+(y+1/n)^2)
(funkcijske vrijednosti ce kvg. k 8 ) i
(xn,yn)=(x-1/n,y-1/n) => f(xn,yn)=((x-1/n)^2+(y-1/n)^2)
(funkcijske vrijednosti kvg k 4)
(dakle f nema limes ni u jednoj tocki (x,y) gdje je x^2+y^2=4)
f je ocito neprekidna u svim tockama (x,y) gdje je x^2+y^2 != 4
Zato je dovoljno provjeriti samo u tockama gdje je x^2+y^2=4
Tu se lako pokaze da f ima prekid u svakoj takvoj tocki, jer mozemo konstruirati dva niza, npr:
(xn,yn)=(x+1/n,y+1/n) => f(xn,yn)=2((x+1/n)^2+(y+1/n)^2)
(funkcijske vrijednosti ce kvg. k 8 ) i
(xn,yn)=(x-1/n,y-1/n) => f(xn,yn)=((x-1/n)^2+(y-1/n)^2)
(funkcijske vrijednosti kvg k 4)
(dakle f nema limes ni u jednoj tocki (x,y) gdje je x^2+y^2=4)
|
|
| [Vrh] |
|
|



















