| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:29 ned, 24. 10. 2010 Naslov: Postano: 22:29 ned, 24. 10. 2010 Naslov: |
    |
|
|
[quote="Black Mamba"]http://web.math.hr/nastava/difraf/dif/2009-10-kol1/kol1_0910.pdf
Može prvi zadatak, bila bi veoma zahvalna? :)[/quote]
a) Možeš uzeti [latex]f, g : \mathbb{R}^2 \to \mathbb{R}[/latex] td. [latex]f(x, y) = x^2 + y^2[/latex] i [latex]g(x, y) = y[/latex]. Očito je [latex]S = f^{-1}(\langle 4, +\infty \rangle) \cap g^{-1}(\langle -\infty, 6 \rangle)[/latex]. Daljnju argumentaciju valjda znaš.
b) Uzmimo [latex]T_0 = (x_0, y_0) \in S[/latex], [latex]r = \min \{ d(0, T_0) - 2, 6 - y_0 \}[/latex]. Neka je [latex]T = (x, y) \in K(T_0, r)[/latex]. Dokažimo [latex]x^2 + y^2 > 4[/latex], što je ekvivalentno s [latex]d(0, T) > 2[/latex]. Vidimo [latex]d(0, T_0) \leq d(0, T) + d(T, T_0)[/latex]. Prebacivanjem dobivamo [latex]d(0, T) \geq d(0, T_0) - d(T, T_0) > d(0, T_0) - r \geq d(0, T_0) - (d(0, T_0) - 2) = 2[/latex]. Da je [latex]y < 6[/latex] probaj dokazati sama.
| Black Mamba (napisa): | http://web.math.hr/nastava/difraf/dif/2009-10-kol1/kol1_0910.pdf
Može prvi zadatak, bila bi veoma zahvalna?  |
a) Možeš uzeti 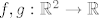 td. td. 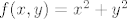 i i 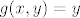 . Očito je . Očito je 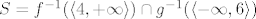 . Daljnju argumentaciju valjda znaš. . Daljnju argumentaciju valjda znaš.
b) Uzmimo 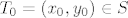 , , 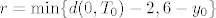 . Neka je . Neka je 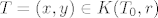 . Dokažimo . Dokažimo 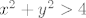 , što je ekvivalentno s , što je ekvivalentno s 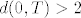 . Vidimo . Vidimo 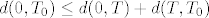 . Prebacivanjem dobivamo . Prebacivanjem dobivamo 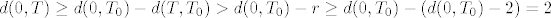 . Da je . Da je 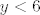 probaj dokazati sama. probaj dokazati sama.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:37 ned, 24. 10. 2010 Naslov: Postano: 23:37 ned, 24. 10. 2010 Naslov: |
    |
|
|
5. a) Da (pogledati skripte iz predavanja o nizovima).
b) Da, da, ne (ista opaska kao gore, samo o neprekidnim fjama na kompaktima).
7. Heine-ova karakterizacija neprekidnosti, limes kvocijenta (iz MA1).
8. Prof. Tambača je dao ideju na predavanju.
Postoji [latex]c \in \bigcap_{i \in I} A_i[/latex]. Neka su [latex]a, b \in \bigcup_{i \in I} A_i[/latex]. Tada postoje [latex]i, j \in I[/latex] td. [latex]a \in A_i[/latex] i [latex]b \in A_j[/latex]. Vidimo da je [latex]c \in A_i[/latex] i [latex]c \in A_j[/latex].
Treba naći put od a do b, a znamo da postoji put od a do c i od c do b. Treba samo još raspisati te puteve, ali to nije neki problem.
5. a) Da (pogledati skripte iz predavanja o nizovima).
b) Da, da, ne (ista opaska kao gore, samo o neprekidnim fjama na kompaktima).
7. Heine-ova karakterizacija neprekidnosti, limes kvocijenta (iz MA1).
8. Prof. Tambača je dao ideju na predavanju.
Postoji 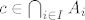 . Neka su . Neka su 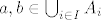 . Tada postoje . Tada postoje 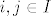 td. td. 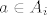 i i 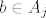 . Vidimo da je . Vidimo da je 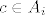 i i 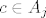 . .
Treba naći put od a do b, a znamo da postoji put od a do c i od c do b. Treba samo još raspisati te puteve, ali to nije neki problem.
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 11:20 pon, 25. 10. 2010 Naslov: Postano: 11:20 pon, 25. 10. 2010 Naslov: |
    |
|
|
[latex]\varepsilon > 0[/latex] proizvoljan. Treba naći [latex]\delta > 0[/latex] td. [latex]\| x - y \| < \delta[/latex] povlači [latex]\| f(x) - f(y) \| < \varepsilon[/latex] za svaki [latex]x, y \in \mathbb{R}^3[/latex]. Očito [latex]\| x - y \| < \delta[/latex] povlači [latex]| x_1 - y_1 | < \delta[/latex], [latex]| x_2 - y_2 | < \delta[/latex] i [latex]| x_3 - y_3 | < \delta[/latex]. Vidimo da je:
[latex]$\begin{align*}
\| f(x) - f(y) \| & = \| ((x_1 - x_3) - (y_1 - y_3), (x_1 + x_2) - (y_1 + y_2)) \| \\
& = \| ((x_1 - y_1) - (x_3 - y_3), (x_1 - y_1) + (x_2 - y_2)) \| \\
& = \| (x_1 - y_1, 0) - (x_3 - y_3, 0) + (0, x_1 - y_1) + (0, x_2 - y_2) \| \\
& \leq \| (x_1 - y_1, 0) \| + \| (x_3 - y_3, 0) \| + \| (0, x_1 - y_1) \| + \| (0, x_2 - y_2) \| \\
& = |x_1 - y_1| + |x_3 - y_3| + |x_1 - y_1| + |x_2 - y_2| \\
& < \delta + \delta + \delta + \delta = 4 \delta
\end{align*}$[/latex]
Znači, dobro je uzeti [latex]\delta = \frac{\varepsilon}{4}[/latex].
 proizvoljan. Treba naći proizvoljan. Treba naći 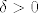 td. td. 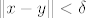 povlači povlači 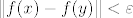 za svaki za svaki 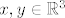 . Očito . Očito 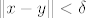 povlači povlači 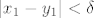 , , 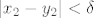 i i 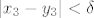 . Vidimo da je: . Vidimo da je:
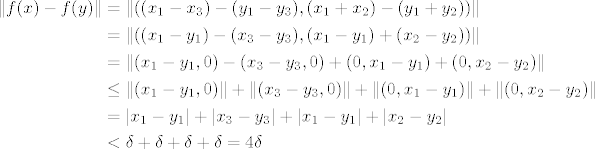
Znači, dobro je uzeti  . .
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
faeton
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:12 pon, 25. 10. 2010 Naslov: Postano: 18:12 pon, 25. 10. 2010 Naslov: |
    |
|
|
[latex]\varepsilon > 0[/latex] proizvoljan. [latex]g : \langle 0, +\infty \rangle \to \langle 0, +\infty \rangle[/latex], [latex]g(z) = z^3 + 2 z^2[/latex] je surjekcija, pa postoji [latex]\delta > 0[/latex] td. [latex]\delta^3 + 2 \delta^2 = \varepsilon[/latex].
[latex]\|(x, y)\| < \delta \ \Rightarrow \ |x| < \delta \, \& \, |y| < \delta[/latex]
[latex]\displaystyle $\begin{align*}
\left| \frac{x^3 y^2 - 2 y^4}{\sqrt{2 x^2 + y^4}} \right| = \frac{| x^3 y^2 - 2 y^4 |}{\sqrt{2 x^2 + y^4}} \leq \frac{| x^3 y^2 | + | 2 y^4 |}{\sqrt{y^4}} = \frac{ |x|^3 y^2 + 2 y^4 }{y^2} = |x|^3 + 2 y^2 < \delta^3 + 2 \delta^2 = \varepsilon
\end{align*}$[/latex]
 proizvoljan. proizvoljan. 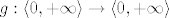 , , 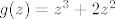 je surjekcija, pa postoji je surjekcija, pa postoji 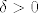 td. td. 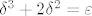 . .

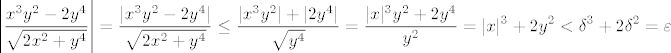
|
|
| [Vrh] |
|
|


















