| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:09 pon, 25. 10. 2010 Naslov: Postano: 19:09 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="eve"]A da nisam koristila polarne koordinate nego neki niz koji konvergira u (0,0) npr (1/n,-1/n), mi onda treba def?[/quote]
Onda da (pritom ne mislim nužno na definiciju, karakterizacija je jednako dobra :)), jer (1/n, -1/n) je poseban niz, a da bi dokazali da je nešto limes, treba pokazati za [b]svaki[/b] niz koji konvergira u točku c (Heine).
| eve (napisa): | | A da nisam koristila polarne koordinate nego neki niz koji konvergira u (0,0) npr (1/n,-1/n), mi onda treba def? |
Onda da (pritom ne mislim nužno na definiciju, karakterizacija je jednako dobra  ), jer (1/n, -1/n) je poseban niz, a da bi dokazali da je nešto limes, treba pokazati za svaki niz koji konvergira u točku c (Heine). ), jer (1/n, -1/n) je poseban niz, a da bi dokazali da je nešto limes, treba pokazati za svaki niz koji konvergira u točku c (Heine).
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 19:12 pon, 25. 10. 2010 Naslov: Postano: 19:12 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="eve"]To me buni malo - kad treba ic na def a kad ne.. A da nisam koristila polarne koordinate nego neki niz koji konvergira u (0,0) npr (1/n,-1/n), mi onda treba def?[/quote]
Tada bi morala provjeriti po definiciji, jer si uzela samo jedan niz u R^2, i pokazala da funkcijske vrijednosti konvergiraju po njemu.
No kada gledaš u polarnim koordinatama, ti se na nikakav način ne ograničavaš (ne gledaš samo neku restrikciju funkcije ili samo neke nizove) nego zapravo samo na drugi način opisuješ stvar.
| eve (napisa): | | To me buni malo - kad treba ic na def a kad ne.. A da nisam koristila polarne koordinate nego neki niz koji konvergira u (0,0) npr (1/n,-1/n), mi onda treba def? |
Tada bi morala provjeriti po definiciji, jer si uzela samo jedan niz u R^2, i pokazala da funkcijske vrijednosti konvergiraju po njemu.
No kada gledaš u polarnim koordinatama, ti se na nikakav način ne ograničavaš (ne gledaš samo neku restrikciju funkcije ili samo neke nizove) nego zapravo samo na drugi način opisuješ stvar.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:47 pon, 25. 10. 2010 Naslov: Postano: 19:47 pon, 25. 10. 2010 Naslov: |
    |
|
|
Radi se o astroidi. Vidi se da je [latex]A \subseteq \overline{K}(0, a)[/latex], pa je ograničen.
Zatvorenost treba pokazati preko konvergencije reda. A niš, uzmemo proizvoljan konvergentan niz u A i treba pokazati da mu je limes u A. Označimo taj niz s [latex]((x_n, y_n))[/latex], a njegov limes s [latex](x, y)[/latex]. Iz toga znamo da [latex]x_n \to x[/latex] i [latex]y_n \to y[/latex]. Vrijedi [latex]\displaystyle x_n^{\frac{2}{3}} + y_n^{\frac{2}{3}} = a^{\frac{2}{3}}[/latex]. Bacimo [latex]\displaystyle \lim_{n \to +\infty}[/latex] na to i dobimo (zbog svojstava limesa) [latex]x^{\frac{2}{3}} + y^{\frac{2}{3}} = a^{\frac{2}{3}}[/latex]. Dakle, x je u A.
Radi se o astroidi. Vidi se da je 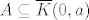 , pa je ograničen. , pa je ograničen.
Zatvorenost treba pokazati preko konvergencije reda. A niš, uzmemo proizvoljan konvergentan niz u A i treba pokazati da mu je limes u A. Označimo taj niz s 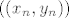 , a njegov limes s , a njegov limes s 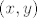 . Iz toga znamo da . Iz toga znamo da 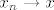 i i 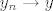 . Vrijedi . Vrijedi 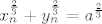 . Bacimo . Bacimo 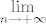 na to i dobimo (zbog svojstava limesa) na to i dobimo (zbog svojstava limesa) 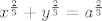 . Dakle, x je u A. . Dakle, x je u A.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 19:54 pon, 25. 10. 2010 Naslov: Postano: 19:54 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="eve"]Ok, sad mi je jasno, hvala!
Jos jedno pitanje, u ovoj zadaci:
http://web.math.hr/nastava/difraf/dif/2007-08/zadaca2_dodatna.pdf
muci me prvi pod a[/quote]
Primijeti da je sa (x1, x2, ... xk) -> x1^(2/3) + ... + xk^(2/3) dana norma na R^n. (Mislim da ne moraš, ali olakšat će posao :)). Činjenicu je vjerujem najlakše pokazati upravo u njoj. S ||.|| i d ću onda označavati tu normu i metriku induciranu njome.
Neka je (xn, yn)n konvergentan niz u A i neka mu je (x, y) limes. Tada je za svaki epsilon d((xn, yn), (x, y)) < ε, za sve n veće od nekog n0, ili drugim rječima: ||(xn, yn) - (x, y)|| < ε, iz cega slijedi: | ||(xn, yn)|| - ||(x, y)|| | < ε, sto je ekvivalentno s -ε < ||(x, y)|| - a^(2/3) < ε, za sve epislon, sto znaci da je norma (x, y) jednaka upravo a^(2/3), i tocka (x, y) se nalazi u skupu A.
Edit: ili naravno puno jednostavnije ovako kako je pmli rekao, ali nisam bio siguran smije li se uopće koristiti činjenica da limes komutira s neprekidnom funkcijom...
Primijeti da je sa (x1, x2, ... xk) → x1^(2/3) + ... + xk^(2/3) dana norma na R^n. (Mislim da ne moraš, ali olakšat će posao  ). Činjenicu je vjerujem najlakše pokazati upravo u njoj. S ||.|| i d ću onda označavati tu normu i metriku induciranu njome. ). Činjenicu je vjerujem najlakše pokazati upravo u njoj. S ||.|| i d ću onda označavati tu normu i metriku induciranu njome.
Neka je (xn, yn)n konvergentan niz u A i neka mu je (x, y) limes. Tada je za svaki epsilon d((xn, yn), (x, y)) < ε, za sve n veće od nekog n0, ili drugim rječima: ||(xn, yn) - (x, y)|| < ε, iz cega slijedi: | ||(xn, yn)|| - ||(x, y)|| | < ε, sto je ekvivalentno s -ε < ||(x, y)|| - a^(2/3) < ε, za sve epislon, sto znaci da je norma (x, y) jednaka upravo a^(2/3), i tocka (x, y) se nalazi u skupu A.
Edit: ili naravno puno jednostavnije ovako kako je pmli rekao, ali nisam bio siguran smije li se uopće koristiti činjenica da limes komutira s neprekidnom funkcijom...
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:25 pon, 25. 10. 2010 Naslov: Postano: 20:25 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="eve"]Fala puno!!
Imam jos jedno pitanje.... U ovom probnom
http://web.math.hr/nastava/difraf/dif/2006-07/probni_kolokvij_1.pdf
3.c?[/quote]
Uzmimo [latex]f, g : [0, 1]^3 \to \mathbb{R}[/latex], [latex]f(x, y, z) = x^2 + 2 y[/latex], [latex]g(x, y, z) = x - y - z[/latex]. Očito je zadani skup jednak [latex]f^{-1}(\{1\}) \cap g^{-1}(\{1\})[/latex]. Svaka od tih praslika je zatvorena u [latex][0, 1]^3[/latex] (jer je {1} zatvoren u [latex]\mathbb{R}[/latex]). Slijedi da su zatvoreni (u [latex]\mathbb{R}^3[/latex]) [size=9](lako se pokaže)[/size]. Znači da je njihov presjek zatvoren, tj. zadani skup. Očito je zadani skup ograničen (podskup je ograničenog) pa je kompaktan.
Uzmimo 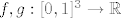 , , 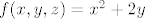 , , 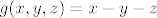 . Očito je zadani skup jednak . Očito je zadani skup jednak  . Svaka od tih praslika je zatvorena u . Svaka od tih praslika je zatvorena u 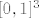 (jer je {1} zatvoren u (jer je {1} zatvoren u  ). Slijedi da su zatvoreni (u ). Slijedi da su zatvoreni (u 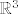 ) (lako se pokaže). Znači da je njihov presjek zatvoren, tj. zadani skup. Očito je zadani skup ograničen (podskup je ograničenog) pa je kompaktan. ) (lako se pokaže). Znači da je njihov presjek zatvoren, tj. zadani skup. Očito je zadani skup ograničen (podskup je ograničenog) pa je kompaktan.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
_student_
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:42 pon, 25. 10. 2010 Naslov: Postano: 22:42 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="_student_"]moze li mi netko pomoci oko 1.d i 1.f zadatka? hvala
http://web.math.hr/nastava/difraf/dif/2008-09/nepr.pdf[/quote]
1.d Preko polarnih i sendviča se može pokazati da ima limes u (0,0) jednak 0.
Sad na x-os bez ishodišta, tj. na točke oblika [latex](x_0, 0)[/latex], gdje je [latex]x_0 \neq 0[/latex]. Vidi se da je [latex]\displaystyle \lim_{(x_0, \frac{1}{n \pi}) \to (x_0, 0)} f(x, y) = \lim_{n \to +\infty} f \left( x_0, \frac{1}{n \pi} \right) = 0[/latex]. Također se vidi [latex]\displaystyle \lim_{(x_0, \frac{1}{\frac{\pi}{2} + 2 n \pi}) \to (x_0, 0)} f(x, y) = \lim_{n \to +\infty} f \left( x_0, \frac{1}{\frac{\pi}{2} + 2 n \pi} \right) = x_0 \sin \frac{1}{x_0}[/latex]. Znači da limes ne postoji u točkama iz skupa [latex]\{ (x_0, 0) : (\forall k \in \mathbb{Z}) \, x_0 \neq \frac{1}{k \pi} \}[/latex].
Preostaje vidjeti što je u točkama oblika [latex](\frac{1}{k \pi}, 0)[/latex], za cjelobrojni k. To možemo shvatiti ovako: "Ima li funkcija [latex]f(x + \frac{1}{k \pi}, y)[/latex] limes u (0,0)?" Opet, kao na početnu, polarnima i sendvičem možemo pokazati da limes postoji i da je jednak 0.
1.f Gledaj posebno limese u točkama skupova [latex]\{ (0, y, z) : y \neq 0\}[/latex], [latex]\{ (0, 0, z) : z \neq 0\}[/latex] i [latex]\{ (0, 0, 0) \}[/latex]. Bazira se na dijelu e).
1.d Preko polarnih i sendviča se može pokazati da ima limes u (0,0) jednak 0.
Sad na x-os bez ishodišta, tj. na točke oblika 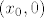 , gdje je , gdje je 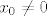 . Vidi se da je . Vidi se da je 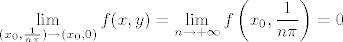 . Također se vidi . Također se vidi 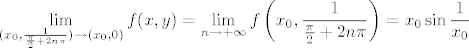 . Znači da limes ne postoji u točkama iz skupa . Znači da limes ne postoji u točkama iz skupa 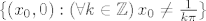 . .
Preostaje vidjeti što je u točkama oblika 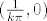 , za cjelobrojni k. To možemo shvatiti ovako: "Ima li funkcija , za cjelobrojni k. To možemo shvatiti ovako: "Ima li funkcija 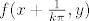 limes u (0,0)?" Opet, kao na početnu, polarnima i sendvičem možemo pokazati da limes postoji i da je jednak 0. limes u (0,0)?" Opet, kao na početnu, polarnima i sendvičem možemo pokazati da limes postoji i da je jednak 0.
1.f Gledaj posebno limese u točkama skupova 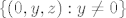 , , 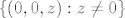 i i 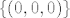 . Bazira se na dijelu e). . Bazira se na dijelu e).
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 18:27 uto, 26. 10. 2010 Naslov: Postano: 18:27 uto, 26. 10. 2010 Naslov: |
    |
|
|
Meni je ispalo
IntS=S
S potez = S unija koordinatne osi unija sve tocke (x,y) za koje je |xy|=1.
gomilista= cijeli S potez
rubS=koordinatne osi i sve tocke (x,y) za koje je |xy|=1.
Za treci, ak se dobro sjecam i ak mi je dobro ispalo, mislim da nema limesa u (0,0)
Meni je ispalo
IntS=S
S potez = S unija koordinatne osi unija sve tocke (x,y) za koje je |xy|=1.
gomilista= cijeli S potez
rubS=koordinatne osi i sve tocke (x,y) za koje je |xy|=1.
Za treci, ak se dobro sjecam i ak mi je dobro ispalo, mislim da nema limesa u (0,0)
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:27 uto, 26. 10. 2010 Naslov: Postano: 18:27 uto, 26. 10. 2010 Naslov: |
    |
|
|
[quote="pajopatak"]Dali bi netko bio dobar i napisao rješenje 1 zd iz današnjeg kolokvija skup S={(x,y): |xy|<1,x!=0,y!=0}[/quote]
Mogu se uzeti tri fje: [latex]f(x,y) = |xy|[/latex], [latex]g(x,y) = x[/latex], [latex]h(x,y) = y[/latex]. Sad je očito [latex]S = f^{-1}(\langle -\infty, 1 \rangle) \cap g^{-1}(\langle -\infty, 0 \rangle \cup \langle 0, +\infty \rangle) \cap h^{-1}(\langle -\infty, 0 \rangle \cup \langle 0, +\infty \rangle)[/latex].
Nekak se i vidi da je [latex]{\sf Int} \, A = A[/latex], [latex]\overline{A} = A' = \{ (x, y) \in \mathbb{R}^2 : |x y| \leq 1 \}[/latex] i [latex]\partial A = \{ (x, y) \in \mathbb{R}^2 : |x y| = 1 \} \cup \{(x, 0) : x \in \mathbb{R} \} \cup \{(0, y) : y \in \mathbb{R} \}[/latex].
[quote="pajopatak"]I dali u u 3.zd postoji limes u (0,0)?[/quote]
Ne. Dobe se različiti limesi za [latex](x, 0) \to (0, 0)[/latex] i [latex](x, x) \to (0, 0)[/latex].
[url=http://www.wolframalpha.com/input/?i=Plot3D%28Sin%28x^3%2F%28x^2%2By^2%29%29%2Fx%2C+{x%2C-1%2C1}%2C+{y%2C-1%2C1}%29]Sliku[/url] je zgodno za vidjeti. :)
| pajopatak (napisa): | | Dali bi netko bio dobar i napisao rješenje 1 zd iz današnjeg kolokvija skup S={(x,y): |xy|<1,x!=0,y!=0} |
Mogu se uzeti tri fje: 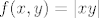 , , 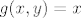 , , 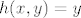 . Sad je očito . Sad je očito 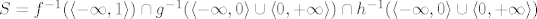 . .
Nekak se i vidi da je 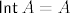 , , 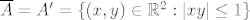 i i 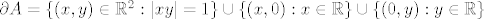 . .
| pajopatak (napisa): | | I dali u u 3.zd postoji limes u (0,0)? |
Ne. Dobe se različiti limesi za 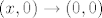 i i 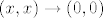 . .
Sliku je zgodno za vidjeti. 
|
|
| [Vrh] |
|
|





















