|
Prvo bi trebalo definirat taj skup, njega cine svi uredeni parovi kojima je prvi element iz {1,2,3} a drugi iz {1,2}
S={(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)}
A onda bi ta relacija bio skup { ((1,1),(1,2)), ((1,1),(1,2)), ((1,1),(2,1)), ...((2,2),(3,2)), ((3,1),(3,2)) }, nisam ih sve pisala al nadam se da je jasno koji bi to jos bili.
I sad treba provjeravat svojstva:
refleksivnost:
[latex](a\leq a) i (b\leq b)
\Longrightarrow (a,b) \rho (a,b)[/latex]
relacija je refleksivna.
simetricnost:
tu se moze nac kontra primjer, npr.:
[latex] (1\leq 2) i (2\leq 2)
\Longrightarrow (1,2)\rho (2,2),
\
(2>1) \Longrightarrow
[/latex]
(2,2) i (1,2) nisu u toj relaciji
antisimetricnost:
[latex]((a,b)\rho (c,d))i ((c,d)\rho (a,b))
\Longrightarrow (a\leq c)i(b\leq d)i(c\leq a)i(d\leq b)
\Longrightarrow (a=c)i(b=d)
\Longrightarrow[/latex]
relacija je antisimetricna.
tranzitivnost:
[latex]((a,b) \rho (c,d))i((c,d)\rho (e,f))
\Longrightarrow ((a\leq c)i(b\leq d)i(c\leq e)i(d\leq f))
\Longrightarrow (a\leq e)i(b\leq f)
\Longrightarrow ((a,b)\rho (e,f))[/latex]
i to je to sto se tice svojstava
A za ovu mjeru meni se cini da je to zadatak
[latex]
\
M ( 3^{2136} - 1, 3^{2138} + 3^{2136}-2)=
\
M ( 3^{2136}-1, 3^{2138}+3^{2136}-2-3^{2136}+1)=
\
M ( 3^{2136}-1, 3^{2138}-1)=
\
M ( 3^{2136}-1,3^{2138}-3^{2136})=
\
M ( 3^{2136}-1, 8\cdot 3^{2136})=
\
M ( 3^{2136}-1,8)=
\
M ( 9^{1068}-1,8)=8[/latex]
Ovaj zadnji = vrijedi jer je 9=8+1 pa kad se to digne na 1068 opet daje ostatak 1 pri djeljenju s 8.
Osim toga mogao bi bit problematican korak kad "maknem" 3^2136 2 reda iznad, ali to je ok buduci da je on relativno prost s 3^2136-1
Ostalo je vise manje cisti Euklidov algoritam.
Prvo bi trebalo definirat taj skup, njega cine svi uredeni parovi kojima je prvi element iz {1,2,3} a drugi iz {1,2}
S={(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)}
A onda bi ta relacija bio skup { ((1,1),(1,2)), ((1,1),(1,2)), ((1,1),(2,1)), ...((2,2),(3,2)), ((3,1),(3,2)) }, nisam ih sve pisala al nadam se da je jasno koji bi to jos bili.
I sad treba provjeravat svojstva:
refleksivnost:
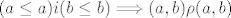
relacija je refleksivna.
simetricnost:
tu se moze nac kontra primjer, npr.:
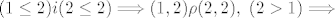
(2,2) i (1,2) nisu u toj relaciji
antisimetricnost:
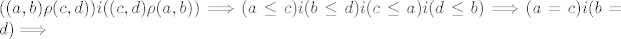
relacija je antisimetricna.
tranzitivnost:
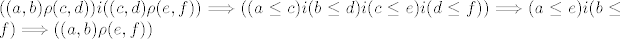
i to je to sto se tice svojstava
A za ovu mjeru meni se cini da je to zadatak
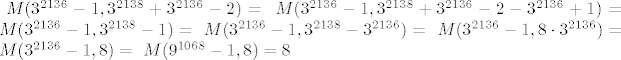
Ovaj zadnji = vrijedi jer je 9=8+1 pa kad se to digne na 1068 opet daje ostatak 1 pri djeljenju s 8.
Osim toga mogao bi bit problematican korak kad "maknem" 3^2136 2 reda iznad, ali to je ok buduci da je on relativno prost s 3^2136-1
Ostalo je vise manje cisti Euklidov algoritam.
|




