| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
 Postano: 17:09 čet, 28. 10. 2010 Naslov: Postano: 17:09 čet, 28. 10. 2010 Naslov: |
    |
|
|
Treći zadatak grupe B od lani neće biti na kolokviju jer to nismo radili (tako mi je rekao asistent), a treći iz grupe A ti ide ovako:
presjek te dvije ravnine je samo jedna točka, recimo da se zove T, pošto je presjek neprazan i samo jedna točka to je ravnina kroz tu točku T smjera W1 presjek W2. Taj smjer je trivijalan, to jest sadrži samo nul vektor pa je jednočlan. Ili možeš, ako ti je draže, reći da je dimenzija presjeka ravnina je 0 (jer sadrži samo točku T), a dimenzija ravnine je dimenzija njenog smjera W1 presjek W2 pa je dimenzija od W1 presjek W2 jednak 0, što značči da sadrži samo nul vektor, što znači da je taj presjek jednočlan skup. Nadam se da je ovo pomoglo. :)
Treći zadatak grupe B od lani neće biti na kolokviju jer to nismo radili (tako mi je rekao asistent), a treći iz grupe A ti ide ovako:
presjek te dvije ravnine je samo jedna točka, recimo da se zove T, pošto je presjek neprazan i samo jedna točka to je ravnina kroz tu točku T smjera W1 presjek W2. Taj smjer je trivijalan, to jest sadrži samo nul vektor pa je jednočlan. Ili možeš, ako ti je draže, reći da je dimenzija presjeka ravnina je 0 (jer sadrži samo točku T), a dimenzija ravnine je dimenzija njenog smjera W1 presjek W2 pa je dimenzija od W1 presjek W2 jednak 0, što značči da sadrži samo nul vektor, što znači da je taj presjek jednočlan skup. Nadam se da je ovo pomoglo. 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pipi
Forumaš(ica)

Pridružen/a: 24. 06. 2010. (19:16:56)
Postovi: (15)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 21:18 čet, 28. 10. 2010 Naslov: Postano: 21:18 čet, 28. 10. 2010 Naslov: |
    |
|
|
[quote="Gino"][quote="c4rimson"]Moze pomoc oko 4.b zadatka iz 2008. godine? Kako odrediti sumu i presijek dviju ravnina?[/quote]
Evo od B grupe.
Iz 4.a) imamo da je [latex]\pi[/latex] ravnina zadana sustavom jednadzbi [latex]\left\{ \begin{array}{l} x_3=0\\ x_4=0\end{arry}\right.[/latex] jasno je da ono sta je u presjeku te ravnine i ravnine zadane sa [latex]x_1+x_2+x_3+x_4=2[/latex] zadovoljava i one jednadzbe i ovu, odnosno presjek je ravnina [latex]\left\{ \begin{array}{ccccccccc} &&&&x_3&&&=&0\\ &&&&&&x_4&=&0\\ x_1&+&x_2&+&x_3&+&x_4&=&2 \end{arry}\right.[/latex], ako to ides zapisat parametarski imas da je to ravnina [latex]\left\{ \begin{array}{l} x_1=t\\x_2=2-t\\x_3=0\\ x_4=0\end{arry}\right.[/latex] pa je jasno da joj je dimenzija [latex]1[/latex], dimenzija od [latex]\pi[/latex] je [latex]2[/latex], od [latex]\pi'[/latex] je [latex]3[/latex], pa jer se sijeku, dimenzija sume je [latex]4[/latex] pa je to [latex]\mathbb{R}^4[/latex][/quote]
kako dobiješ 4.a)? i kak se provjerava da li je točka u ravnini? :oops:
| Gino (napisa): | | c4rimson (napisa): | | Moze pomoc oko 4.b zadatka iz 2008. godine? Kako odrediti sumu i presijek dviju ravnina? |
Evo od B grupe.
Iz 4.a) imamo da je  ravnina zadana sustavom jednadzbi ravnina zadana sustavom jednadzbi 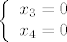 jasno je da ono sta je u presjeku te ravnine i ravnine zadane sa jasno je da ono sta je u presjeku te ravnine i ravnine zadane sa 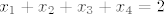 zadovoljava i one jednadzbe i ovu, odnosno presjek je ravnina zadovoljava i one jednadzbe i ovu, odnosno presjek je ravnina 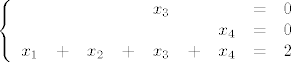 , ako to ides zapisat parametarski imas da je to ravnina , ako to ides zapisat parametarski imas da je to ravnina 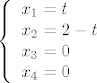 pa je jasno da joj je dimenzija pa je jasno da joj je dimenzija  , dimenzija od , dimenzija od  je je  , od , od 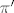 je je 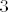 , pa jer se sijeku, dimenzija sume je , pa jer se sijeku, dimenzija sume je 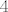 pa je to pa je to 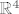 |
kako dobiješ 4.a)? i kak se provjerava da li je točka u ravnini? 
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pipi
Forumaš(ica)

Pridružen/a: 24. 06. 2010. (19:16:56)
Postovi: (15)16
|
|
| [Vrh] |
|
bucko
Forumaš(ica)


Pridružen/a: 04. 12. 2007. (20:55:30)
Postovi: (A9)16
Spol: 
|
|
| [Vrh] |
|
pipi
Forumaš(ica)

Pridružen/a: 24. 06. 2010. (19:16:56)
Postovi: (15)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pipi
Forumaš(ica)

Pridružen/a: 24. 06. 2010. (19:16:56)
Postovi: (15)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Malina_1
Forumaš(ica)
Pridružen/a: 26. 01. 2010. (22:06:23)
Postovi: (23)16
|
|
| [Vrh] |
|
čungalunga
Forumaš(ica)


Pridružen/a: 25. 11. 2009. (20:50:12)
Postovi: (4C)16
Spol: 
Lokacija: varaždin/zagreb
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 20:17 sri, 12. 1. 2011 Naslov: Postano: 20:17 sri, 12. 1. 2011 Naslov: |
    |
|
|
[quote="čungalunga"]kak se rješava 1. zad s prošlog kolokvija?
http://web.math.hr/nastava/eukl/pismeni/GrupaA.pdf[/quote]
E sad... jednom sam znal, al bi ja ovak probo:
prvo ću označit točke:
[latex] ( 0, 0 ) - O \hspace{5mm} ( 1, 0 ) - E_1 \hspace{5mm} ( 0, 1 ) - E_2\\ ( a, a+1 ) - O^{'} \hspace{5mm} ( 1, a ) - E_1^{'} \hspace{5mm} ( a, 0 ) - E_2^{'}[/latex]
u zadatku je dano:
[latex]f_a( O ) = O^{'} \\ f_a( E_1 ) = E_1^{'} \\ f_a( E_2 ) = E_2^{'}[/latex]
i s obzirom da je [latex]f_a[/latex] afino preslikavanje, onda postoji linearan operator [latex]\rho[/latex] t.d. je:
[latex]( 1 - a, -1 ) =[/latex][latex]\displaystyle{\over{f_a( O )f_a( E_1 )}}[/latex][latex]= \rho[/latex][latex]\displaystyle{ \over{(OE_1} )}}[/latex]
[latex]( 0, -1-a ) =[/latex][latex]\displaystyle{\over{f_a( O )f_a( E_2 )}}[/latex][latex]= \rho[/latex][latex]\displaystyle{ \over{(OE_2} )}}[/latex]
s obzirom da vrijedi:
[latex]f_a[/latex] je injekcija <=> [latex]\rho[/latex] je injekcija
tj. treba dokazati da je [latex]\rho[/latex] injekcija.
Na linearnoj algebri smo učili da injektivni operator linearno nezavisne skupove prebacuje u linearno nezavisne skupove, tj. trebaš provjerit za koje [latex]a \in \mathbb{R}[/latex] vrijedi da je:
[latex]\{(1-a, -1) , ( 0, -1-a ) \}[/latex]
linearno nezavisan skup. To ti ostavljam.
kod b) djela treba pogledat za koje je [latex]a \in \mathbb{R}[/latex] preslikavanje [latex]\rho[/latex] izometrija.
E sad... jednom sam znal, al bi ja ovak probo:
prvo ću označit točke:
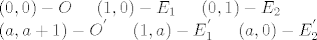
u zadatku je dano:
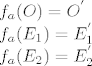
i s obzirom da je 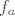 afino preslikavanje, onda postoji linearan operator afino preslikavanje, onda postoji linearan operator 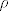 t.d. je: t.d. je:
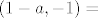 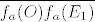 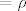 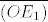
 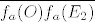 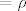 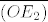
s obzirom da vrijedi:
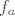 je injekcija ⇔ je injekcija ⇔ 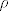 je injekcija je injekcija
tj. treba dokazati da je 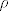 injekcija. injekcija.
Na linearnoj algebri smo učili da injektivni operator linearno nezavisne skupove prebacuje u linearno nezavisne skupove, tj. trebaš provjerit za koje 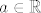 vrijedi da je: vrijedi da je:
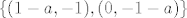
linearno nezavisan skup. To ti ostavljam.
kod b) djela treba pogledat za koje je 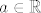 preslikavanje preslikavanje 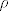 izometrija. izometrija.
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
|









