| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tierra
Forumaš(ica)


Pridružen/a: 07. 11. 2007. (12:46:15)
Postovi: (4D)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
lim
Gost
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 0:50 čet, 4. 11. 2010 Naslov: Re: zadatak s minimalnim polinomom Postano: 0:50 čet, 4. 11. 2010 Naslov: Re: zadatak s minimalnim polinomom |
    |
|
|
[quote="tierra"]gledam ja zadatak i on gleda mene i nemamo ni on ni ja ideju kako ga riješit...
pa molim pomoć oko ideje, ne treba rješavat baš zadatak...
ovako: zadatak je sa kolokvija iz 2008.
jedna grupa ima zadan minimalni polinom nekog operatora A i on je x^2 + x + 1 , a treba izračunat minimalni za A + 3I...
a druga grupa minimalni polinom op.A koji je x^3 + x^2 +1
a treba izračunat minimalni od A - 2I[/quote]
ja sam to ovak... mislim da bi to tak trebalo ić, al nisam ziher
( uzet ću ovaj lakši zbog raspisivanja )
znači:
[latex]\mu_A(x) = x^2 + x + 1[/latex]
tj.
[latex]A^2 + A + I = 0[/latex]
jer se A poništava u minimalnom polinomu. Treba naći minimalini od: A + 3I
[latex] (A + 3I)^2 = A^2 + 6A + 9I[/latex]
pa iz: [latex]A^2 + A + I = 0[/latex] proizlazi:
[latex]0 = A^2 + 6A + 9I - 5A -8I = ( A + 3I )^2 -5A -8I = ( A + 3I )^2 -5( A + 3I ) + 7I [/latex]
tj.
[latex]( A + 3I )^2 -5( A + 3I ) + 7I = 0[/latex]
pa stavim da je:
[latex]\mu_{A+3I}( x ) = x^2 - 5x + 7[/latex]
3. zadatak ne znam, tj. znam dokazat onu jednakost ak pretpostavim da sam dokazao da je A + N invertibilan, a 10. sam napiso prve 3 do 4 potencije i onda već mogu naslutiti rješenje. ( jedan takav sam rješio, a na drugom sam dobio za jedan element rekurziju koja mi se baš i nije dala rješavat )
| tierra (napisa): | gledam ja zadatak i on gleda mene i nemamo ni on ni ja ideju kako ga riješit...
pa molim pomoć oko ideje, ne treba rješavat baš zadatak...
ovako: zadatak je sa kolokvija iz 2008.
jedna grupa ima zadan minimalni polinom nekog operatora A i on je x^2 + x + 1 , a treba izračunat minimalni za A + 3I...
a druga grupa minimalni polinom op.A koji je x^3 + x^2 +1
a treba izračunat minimalni od A - 2I |
ja sam to ovak... mislim da bi to tak trebalo ić, al nisam ziher
( uzet ću ovaj lakši zbog raspisivanja )
znači:
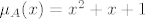
tj.
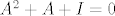
jer se A poništava u minimalnom polinomu. Treba naći minimalini od: A + 3I
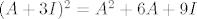
pa iz: 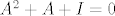 proizlazi: proizlazi:
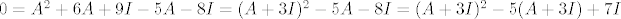
tj.
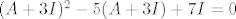
pa stavim da je:
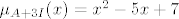
3. zadatak ne znam, tj. znam dokazat onu jednakost ak pretpostavim da sam dokazao da je A + N invertibilan, a 10. sam napiso prve 3 do 4 potencije i onda već mogu naslutiti rješenje. ( jedan takav sam rješio, a na drugom sam dobio za jedan element rekurziju koja mi se baš i nije dala rješavat )
|
|
| [Vrh] |
|
Thor
Forumaš(ica)


Pridružen/a: 24. 04. 2009. (10:57:50)
Postovi: (15)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
missy
Gost
|
|
| [Vrh] |
|
Thor
Forumaš(ica)


Pridružen/a: 24. 04. 2009. (10:57:50)
Postovi: (15)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
:)
Forumaš(ica)
Pridružen/a: 25. 04. 2009. (16:17:14)
Postovi: (66)16
|
|
| [Vrh] |
|
Thor
Forumaš(ica)


Pridružen/a: 24. 04. 2009. (10:57:50)
Postovi: (15)16
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
:)
Forumaš(ica)
Pridružen/a: 25. 04. 2009. (16:17:14)
Postovi: (66)16
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
tierra
Forumaš(ica)


Pridružen/a: 07. 11. 2007. (12:46:15)
Postovi: (4D)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
|










