|
Pošto je [latex]1001=7 \cdot 11 \cdot 13[/latex], vidimo da je ostatak pri dijeljenju broja [latex]1000[/latex] sa [latex]7[/latex], [latex]11[/latex] i [latex]13[/latex] jednak [latex]-1[/latex].
Sada zaključujemo da je broj [latex]n=\overline{a_{3k}a_{3k-1}a_{3k-2}\ldots a_3a_2a_1}[/latex] (nadopunimo ga vodećim nulama da dobijemo da mu je broj znamenki djeljiv s [latex]3[/latex]) djeljiv sa [latex]7[/latex], [latex]11[/latex], [latex]13[/latex] ako i samo ako je broj [latex]\overline{a_3a_2a_1}-\overline{a_6a_5a_4}+\ldots \pm \overline{a_{3k}a_{3k-1}a_{3k-2}}[/latex] djeljiv sa [latex]7[/latex], [latex]11[/latex], [latex]13[/latex]. (U tom poretku.)
Za [latex]7[/latex] i [latex]11[/latex] postoje još i ovi pitomiji kriteriji.
Prirodan broj [latex]n[/latex] je djeljiv sa [latex]7[/latex] ako i samo ako je broj [latex]m[/latex] djeljiv sa [latex]7[/latex]. Broj [latex]m[/latex] se iz broja [latex]n[/latex] dobije tako da mu se ispusti znamenka jedinica i onda se dobivenom broju oduzme dvostruka ta znamenka.
Npr. za [latex]n=14[/latex], [latex]m=-7[/latex], za [latex]n=1001[/latex], [latex]m=98[/latex], [latex]m_1=-7[/latex]...
Dokaz ove činjenice proizlazi iz toga da je [latex]10 \equiv 3 \pmod{7}[/latex], zato je [latex]10x + y \equiv 3x + y \equiv 6x+2y \equiv -x+2y \equiv x - 2y \pmod{7} [/latex].
Prirodan broj [latex]n=\overline{a_ka_{k-1}\ldots a_1}[/latex] je djeljiv s [latex]11[/latex] ako i samo ako je broj [latex]a_1-a2+\ldots \pm a_k[/latex] djeljiv s 11.
Ovo proizlazli direktno iz činjenice da je [latex]10 \equiv -1 \pmod{11}[/latex].
Za [latex]19[/latex] vrijedi sličan kriterij kao ovaj pitomiji za [latex]7[/latex], samo što ne oduzmemo dvostruku znamenku nego ju dodamo...
Npr. [latex]n=38[/latex], [latex]m=19[/latex]; [latex]n=209[/latex], [latex]m=38[/latex], [latex]m_1=19[/latex]...
Dokaz ide direktno iz
[latex]10x+y \equiv 20x+2y \equiv x+2y \pmod{19}[/latex].
Pošto je 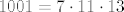 , vidimo da je ostatak pri dijeljenju broja , vidimo da je ostatak pri dijeljenju broja 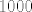 sa sa 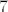 , , 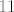 i i 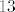 jednak jednak  . .
Sada zaključujemo da je broj 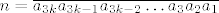 (nadopunimo ga vodećim nulama da dobijemo da mu je broj znamenki djeljiv s (nadopunimo ga vodećim nulama da dobijemo da mu je broj znamenki djeljiv s 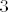 ) djeljiv sa ) djeljiv sa 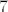 , , 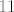 , , 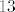 ako i samo ako je broj ako i samo ako je broj 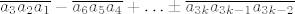 djeljiv sa djeljiv sa 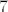 , , 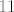 , , 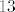 . (U tom poretku.) . (U tom poretku.)
Za 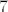 i i 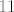 postoje još i ovi pitomiji kriteriji. postoje još i ovi pitomiji kriteriji.
Prirodan broj  je djeljiv sa je djeljiv sa 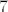 ako i samo ako je broj ako i samo ako je broj  djeljiv sa djeljiv sa 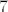 . Broj . Broj  se iz broja se iz broja  dobije tako da mu se ispusti znamenka jedinica i onda se dobivenom broju oduzme dvostruka ta znamenka. dobije tako da mu se ispusti znamenka jedinica i onda se dobivenom broju oduzme dvostruka ta znamenka.
Npr. za  , ,  , za , za  , ,  , , 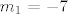 ... ...
Dokaz ove činjenice proizlazi iz toga da je 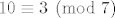 , zato je , zato je 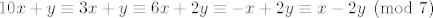 . .
Prirodan broj 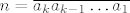 je djeljiv s je djeljiv s 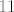 ako i samo ako je broj ako i samo ako je broj  djeljiv s 11. djeljiv s 11.
Ovo proizlazli direktno iz činjenice da je 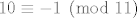 . .
Za 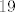 vrijedi sličan kriterij kao ovaj pitomiji za vrijedi sličan kriterij kao ovaj pitomiji za 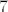 , samo što ne oduzmemo dvostruku znamenku nego ju dodamo... , samo što ne oduzmemo dvostruku znamenku nego ju dodamo...
Npr.  , ,  ; ; 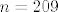 , ,  , , 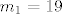 ... ...
Dokaz ide direktno iz
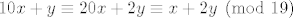 . .
|




