|
Nema nekog generalnog načina - čisto po definiciji, niz je ograničen ako možeš pronaći neki njegovu donju među i neku njegovu gornju među. Ako pomaže, ograničenost niza je ekvivalentna s tim da niti jedan njegov podniz ne divergira u neku od beskonačnosti. Dakle, možeš na primjer pokazati da niz nije omeđen ako pronađeš neki njegov podniz koji ide u [latex]\pm \infty[/latex].
Također, jedan od lakših načina (koji očito nije primjenjiv na svim nizovima, ali vrlo često djeluje u nekim lakšim primjerima) je pogledati postaje li niz nakon konačno mnogo članova rastući/padajuć. Ako nakon nekog vremena počne padati, to očito znači da je ograničen odozgo, a ako nakon nekog vremena počne rasti, to znači da je ograničen odozdo. Naravno, ako je niz padajuć, ne možemo općenito ništa reći o njegovoj ograničenosti odozdo i obrnuto (za rastuće nizove).
Zapravo, ideja je da iskoristiš kombinaciju svih tih ideja. Specifično, u tvom slučaju, pokazat ćemo da su svi članovi niza nepozitivni (što znači da je [latex]0[/latex] gornja međa), kao i da su svi veći od [latex]-1[/latex] (što znači da je ograničen i odozdo).
Inače, ako ne pišeš u TeXu, stavi neke zagrade da bude jasno kako izgleda član niza. Po ovome što si ti napisao bez zagrada, član bi zapravo bio [latex]x_n=1-\frac{1}{n}[/latex], ali pretpostavljam da u tom slučaju ne bi bio tako zadan. Dakle, uzet ću da si htio reći [latex]x_n=\displaystyle\frac{1-n}{n^2}[/latex]. Pogledajmo sad čemu je ekvivalentno [latex]x_n\leq 0[/latex]. Možemo pomnožiti obje strane s [latex]n^2[/latex], pa imamo [latex]1-n\leq 0[/latex], tj. [latex]n\geq 1[/latex], što svakako stoji.
S druge strane, [latex]x_n>-1[/latex] je ekvivalentno [latex]1-n>-n^2[/latex], tj. [latex]n^2-n+1>0[/latex]. Lako se pokaže da ovo vrijedi za sve prirodne (pa čak i za sve realne - pogledaj diskriminantu u pripadajućoj kvadratnoj jednadžbi) brojeve, pa i ovo stoji.
Evo, pokazali smo da su svi članovi niza u intervalu [latex]\langle -1,0][/latex] pa je niz ograničen. Mogli smo pronaći i manji interval (mislim da je [latex]\left[-\frac{1}{4},0\right][/latex] zapravo najmanji interval koji sadrži sve članove niza), ali to nas se u ovom trenutku ne pita.
Nema nekog generalnog načina - čisto po definiciji, niz je ograničen ako možeš pronaći neki njegovu donju među i neku njegovu gornju među. Ako pomaže, ograničenost niza je ekvivalentna s tim da niti jedan njegov podniz ne divergira u neku od beskonačnosti. Dakle, možeš na primjer pokazati da niz nije omeđen ako pronađeš neki njegov podniz koji ide u  . .
Također, jedan od lakših načina (koji očito nije primjenjiv na svim nizovima, ali vrlo često djeluje u nekim lakšim primjerima) je pogledati postaje li niz nakon konačno mnogo članova rastući/padajuć. Ako nakon nekog vremena počne padati, to očito znači da je ograničen odozgo, a ako nakon nekog vremena počne rasti, to znači da je ograničen odozdo. Naravno, ako je niz padajuć, ne možemo općenito ništa reći o njegovoj ograničenosti odozdo i obrnuto (za rastuće nizove).
Zapravo, ideja je da iskoristiš kombinaciju svih tih ideja. Specifično, u tvom slučaju, pokazat ćemo da su svi članovi niza nepozitivni (što znači da je  gornja međa), kao i da su svi veći od gornja međa), kao i da su svi veći od  (što znači da je ograničen i odozdo). (što znači da je ograničen i odozdo).
Inače, ako ne pišeš u TeXu, stavi neke zagrade da bude jasno kako izgleda član niza. Po ovome što si ti napisao bez zagrada, član bi zapravo bio 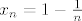 , ali pretpostavljam da u tom slučaju ne bi bio tako zadan. Dakle, uzet ću da si htio reći , ali pretpostavljam da u tom slučaju ne bi bio tako zadan. Dakle, uzet ću da si htio reći 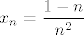 . Pogledajmo sad čemu je ekvivalentno . Pogledajmo sad čemu je ekvivalentno  . Možemo pomnožiti obje strane s . Možemo pomnožiti obje strane s 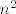 , pa imamo , pa imamo 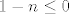 , tj. , tj. 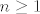 , što svakako stoji. , što svakako stoji.
S druge strane,  je ekvivalentno je ekvivalentno 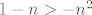 , tj. , tj. 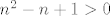 . Lako se pokaže da ovo vrijedi za sve prirodne (pa čak i za sve realne - pogledaj diskriminantu u pripadajućoj kvadratnoj jednadžbi) brojeve, pa i ovo stoji. . Lako se pokaže da ovo vrijedi za sve prirodne (pa čak i za sve realne - pogledaj diskriminantu u pripadajućoj kvadratnoj jednadžbi) brojeve, pa i ovo stoji.
Evo, pokazali smo da su svi članovi niza u intervalu 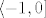 pa je niz ograničen. Mogli smo pronaći i manji interval (mislim da je pa je niz ograničen. Mogli smo pronaći i manji interval (mislim da je 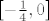 zapravo najmanji interval koji sadrži sve članove niza), ali to nas se u ovom trenutku ne pita. zapravo najmanji interval koji sadrži sve članove niza), ali to nas se u ovom trenutku ne pita.
|







