| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 12:13 čet, 18. 11. 2010 Naslov: Kom da se obratim? Postano: 12:13 čet, 18. 11. 2010 Naslov: Kom da se obratim? |
    |
|
|
Jedno pitanje samo. Imo sam kolokvij iz vektorskih prostora i jedan zadatak koji sam po mojem rješio točno, a po asistentovom netočno. Znači rješenje mi je potpuno točno, ali imam 0 bodova. Išo sam do profesora i on i je rekao da mi ne može tu pomoći jer je to asistentov zadatak ( ne točno tim riječima al sam tako zaključio ).
Zadatak glasi: Imamo operator A i njegov matrični prikaz. Treba naći minimalni polinom pomoću algoritma koji smo radili na vježbama. Znači pomoću matrica [latex]A_{i,j}[/latex]
gdje je:
[latex]A_{j+1,k} = A_{j,k} - \alpha \cdot A_{j,j}[/latex]
U zadatku s kolokvija smo dobili matricu A takvu da je [latex]A^{2} = A^{3}[/latex].
S obzirom da sam ja prvo računo sve potencije ( znači do [latex]A^3[/latex] ) jer je A reda 3, zaključio sam da umjesto da bespotrebno pišem matrice [latex]A_{i,j}[/latex] mogu napisati ovo:
[latex]A^3 - A^2 = 0[/latex]
te da to povlači...
[latex]\mu_A(x) = x^3 - x^2[/latex]
Točno tako sam napisao u zadatku. E sad po meni je to rješenje u potpunosti točno rješenje jer u algoritmu se nigdje ne kaže što moram prvo... gledat potencije matrice A ili matrice [latex]A_{i,j}[/latex].
Nama je napomenuto da je "pametnije" prvo gledat matrice [latex]A_{i,j}[/latex] jer se eventualno može desiti da sam prije one zadnje matrice dobio da mi je neka i,j matrica jednaka nul-matrici i mogu stati s algoritmom, pa nije potrbno gledati veće potencije. Asistent nije to rekao ali po broju bodova ( 0 ) mogu zaključiti da on moje rješenje smatra potpuno netočnim. Profesor ne može pomoć kako kaže pa me zanima kom da se dalje obratim? ( il ak mislite da nemam nekih temelja za daljnje žaljenje recite ).
Inače moje mišljenje je da ako je asistent htio da konkretno napišem cijeli algoritam mogo je bar izabrat neku matricu za koju mi je to i potrebno.
Jedno pitanje samo. Imo sam kolokvij iz vektorskih prostora i jedan zadatak koji sam po mojem rješio točno, a po asistentovom netočno. Znači rješenje mi je potpuno točno, ali imam 0 bodova. Išo sam do profesora i on i je rekao da mi ne može tu pomoći jer je to asistentov zadatak ( ne točno tim riječima al sam tako zaključio ).
Zadatak glasi: Imamo operator A i njegov matrični prikaz. Treba naći minimalni polinom pomoću algoritma koji smo radili na vježbama. Znači pomoću matrica 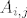
gdje je:
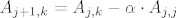
U zadatku s kolokvija smo dobili matricu A takvu da je 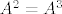 . .
S obzirom da sam ja prvo računo sve potencije ( znači do 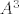 ) jer je A reda 3, zaključio sam da umjesto da bespotrebno pišem matrice ) jer je A reda 3, zaključio sam da umjesto da bespotrebno pišem matrice 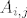 mogu napisati ovo: mogu napisati ovo:
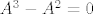
te da to povlači...
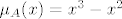
Točno tako sam napisao u zadatku. E sad po meni je to rješenje u potpunosti točno rješenje jer u algoritmu se nigdje ne kaže što moram prvo... gledat potencije matrice A ili matrice 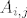 . .
Nama je napomenuto da je "pametnije" prvo gledat matrice 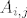 jer se eventualno može desiti da sam prije one zadnje matrice dobio da mi je neka i,j matrica jednaka nul-matrici i mogu stati s algoritmom, pa nije potrbno gledati veće potencije. Asistent nije to rekao ali po broju bodova ( 0 ) mogu zaključiti da on moje rješenje smatra potpuno netočnim. Profesor ne može pomoć kako kaže pa me zanima kom da se dalje obratim? ( il ak mislite da nemam nekih temelja za daljnje žaljenje recite ). jer se eventualno može desiti da sam prije one zadnje matrice dobio da mi je neka i,j matrica jednaka nul-matrici i mogu stati s algoritmom, pa nije potrbno gledati veće potencije. Asistent nije to rekao ali po broju bodova ( 0 ) mogu zaključiti da on moje rješenje smatra potpuno netočnim. Profesor ne može pomoć kako kaže pa me zanima kom da se dalje obratim? ( il ak mislite da nemam nekih temelja za daljnje žaljenje recite ).
Inače moje mišljenje je da ako je asistent htio da konkretno napišem cijeli algoritam mogo je bar izabrat neku matricu za koju mi je to i potrebno.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 12:41 čet, 18. 11. 2010 Naslov: Postano: 12:41 čet, 18. 11. 2010 Naslov: |
    |
|
|
Ajme, sjecam se toga od prosle godine. Meni je bio skidao (iako, mislim ne sve) bodove jer sam iz predzadnjeg reda zakljucio sto je rjesenje. Naime, njegov argument je bio: "Vi niste proveli algoritam do kraja" :lol: Sretno sa daljnim zalbama :)
EDIT: Sad kad bolje promislim mislim da su ljudi i za jos gluplje stvari na tim zadacima gubili bodove. U stilu, nisu numerirali matrice isto kao i on. Opet, argument njegov: "Vi niste proveli algoritam". Ne, uopce nema veze sto algoritam funkcionira i ako varijable drukcije nazovem.
Eto, nisam od pomoci, ali da olaksam dusu :)
Ajme, sjecam se toga od prosle godine. Meni je bio skidao (iako, mislim ne sve) bodove jer sam iz predzadnjeg reda zakljucio sto je rjesenje. Naime, njegov argument je bio: "Vi niste proveli algoritam do kraja"  Sretno sa daljnim zalbama Sretno sa daljnim zalbama 
EDIT: Sad kad bolje promislim mislim da su ljudi i za jos gluplje stvari na tim zadacima gubili bodove. U stilu, nisu numerirali matrice isto kao i on. Opet, argument njegov: "Vi niste proveli algoritam". Ne, uopce nema veze sto algoritam funkcionira i ako varijable drukcije nazovem.
Eto, nisam od pomoci, ali da olaksam dusu 
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 15:28 čet, 18. 11. 2010 Naslov: Postano: 15:28 čet, 18. 11. 2010 Naslov: |
    |
|
|
[quote]Kom da se obratim?[/quote]
Po [url=http://www.math.hr/lgs.axd?t=16&id=2780]statutu[/url], članak 36. prvo bi se trebao obratiti prodekanu za nastavu, a onda (vjerojatno ako ta žalba ne upali ili i dalje smatraš da si zakinut) dekanu.
No. s obzirom da je u zadatku pisalo "Koristeći algoritam za traženje minimalnog polinoma, odredite...", sumnjam da će se žalba riješiti u tvoju korist.
Btw. malo sam zahrđao u vektorskima, no ako je A^3-A^2=0, ne znači li to da minimalni polinom od A dijeli x^3-x^2 pa se faktoriziranjem tog polinoma nad C pokaže da je to stvarno polinom najmanjeg stupnja koji poništava A, tj. ne može se, za općenitu matricu A reći da A^3-A^2=0 povlači da je minimalni polinom x^3-x^2 (kontraprimjer je jedinična matrica)?
| Citat: | | Kom da se obratim? |
Po statutu, članak 36. prvo bi se trebao obratiti prodekanu za nastavu, a onda (vjerojatno ako ta žalba ne upali ili i dalje smatraš da si zakinut) dekanu.
No. s obzirom da je u zadatku pisalo "Koristeći algoritam za traženje minimalnog polinoma, odredite...", sumnjam da će se žalba riješiti u tvoju korist.
Btw. malo sam zahrđao u vektorskima, no ako je A^3-A^2=0, ne znači li to da minimalni polinom od A dijeli x^3-x^2 pa se faktoriziranjem tog polinoma nad C pokaže da je to stvarno polinom najmanjeg stupnja koji poništava A, tj. ne može se, za općenitu matricu A reći da A^3-A^2=0 povlači da je minimalni polinom x^3-x^2 (kontraprimjer je jedinična matrica)?
_________________
The Dude Abides
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 18:30 čet, 18. 11. 2010 Naslov: Postano: 18:30 čet, 18. 11. 2010 Naslov: |
    |
|
|
[quote="goranm"]
No. s obzirom da je u zadatku pisalo "Koristeći algoritam za traženje minimalnog polinoma, odredite...", sumnjam da će se žalba riješiti u tvoju korist.
Btw. malo sam zahrđao u vektorskima, no ako je A^3-A^2=0, ne znači li to da minimalni polinom od A dijeli x^3-x^2 pa se faktoriziranjem tog polinoma nad C pokaže da je to stvarno polinom najmanjeg stupnja koji poništava A, tj. ne može se, za općenitu matricu A reći da A^3-A^2=0 povlači da je minimalni polinom x^3-x^2 (kontraprimjer je jedinična matrica)?[/quote]
pa u algoritmu se traži da pronađem potencije matrice što sam i napravio. Znači naglašavam krenuo sam s algoritmom i došao do rješenja. To što je zadatak bio zadan na taj način da ja odmah vidim rješenje nije moj problem i nije mi jasno zašto sam onda i zakinut na tome što sam to i napisao. Općenito kad imam zadatak računam i gledam samo ono što mi treba, kad u nekom smjeru dođem do djela kad mi daljnje računanje nije potrebno za rješenje ni ne vidim smisao daljnjeg računanja. Zašto bi rješavao algoritam do kraja ako sam već dobio rješenje par koraka prije?
I mogu odmah zakljucit da mi je to minimalni polinom jer mi je [latex]A \neq A^2[/latex] i A mi nije jedinicna matrica, no to nisam napisao jer sam napisao što je [latex]A[/latex], što je [latex]A^2[/latex] i što je [latex]A^3[/latex], pa nisam eksplicitno pisao što je jednako ili nije jednako, naravno osim [latex]A^2 = A^3[/latex] što mi je potrebno za rješenje.
Hvala na odgovoru.
| goranm (napisa): |
No. s obzirom da je u zadatku pisalo "Koristeći algoritam za traženje minimalnog polinoma, odredite...", sumnjam da će se žalba riješiti u tvoju korist.
Btw. malo sam zahrđao u vektorskima, no ako je A^3-A^2=0, ne znači li to da minimalni polinom od A dijeli x^3-x^2 pa se faktoriziranjem tog polinoma nad C pokaže da je to stvarno polinom najmanjeg stupnja koji poništava A, tj. ne može se, za općenitu matricu A reći da A^3-A^2=0 povlači da je minimalni polinom x^3-x^2 (kontraprimjer je jedinična matrica)? |
pa u algoritmu se traži da pronađem potencije matrice što sam i napravio. Znači naglašavam krenuo sam s algoritmom i došao do rješenja. To što je zadatak bio zadan na taj način da ja odmah vidim rješenje nije moj problem i nije mi jasno zašto sam onda i zakinut na tome što sam to i napisao. Općenito kad imam zadatak računam i gledam samo ono što mi treba, kad u nekom smjeru dođem do djela kad mi daljnje računanje nije potrebno za rješenje ni ne vidim smisao daljnjeg računanja. Zašto bi rješavao algoritam do kraja ako sam već dobio rješenje par koraka prije?
I mogu odmah zakljucit da mi je to minimalni polinom jer mi je 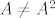 i A mi nije jedinicna matrica, no to nisam napisao jer sam napisao što je i A mi nije jedinicna matrica, no to nisam napisao jer sam napisao što je  , što je , što je 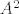 i što je i što je 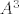 , pa nisam eksplicitno pisao što je jednako ili nije jednako, naravno osim , pa nisam eksplicitno pisao što je jednako ili nije jednako, naravno osim 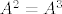 što mi je potrebno za rješenje. što mi je potrebno za rješenje.
Hvala na odgovoru.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:21 čet, 18. 11. 2010 Naslov: Postano: 19:21 čet, 18. 11. 2010 Naslov: |
    |
|
|
:OT:
[quote="Cobs"] I mogu odmah zakljucit da mi je to minimalni polinom jer mi je [latex]A \neq A^2[/latex] i A mi nije jedinicna matrica, no to nisam napisao jer sam napisao što je [latex]A[/latex], što je [latex]A^2[/latex] i što je [latex]A^3[/latex], pa nisam eksplicitno pisao što je jednako ili nije jednako, naravno osim [latex]A^2 = A^3[/latex] što mi je potrebno za rješenje.[/quote]
Ne znam da li pričamo o istoj stvari; samo iz toga što si napisao [b]na papiru[/b] (drugo je što u glavi vidiš da nema drugih mogućnosti osim baš te koju si napisao) ne možeš zaključiti da je minimalni polinom [latex]x^3-x^2[/latex] jer postoje matrice za koje vrijedi [latex]A\neq I,~A \neq A^2[/latex] i [latex]A^2=A^3[/latex], ali minimalni polinom im nije [latex]x^3-x^2[/latex].
Da je [latex]A^2=A^3[/latex] povlači [latex]\mu_A(x)|x^3-x^2=x^2(x-1)[/latex] pa ili je [latex]x^3-x^2[/latex] minimalni polinom ili je A nilpotentna indeksa 2 ili je A=I. Budući da zadnja dva slučaja ne vrijede, tek onda slijedi da je [latex]\mu_A(x)=x^3-x^2[/latex]

| Cobs (napisa): | I mogu odmah zakljucit da mi je to minimalni polinom jer mi je 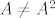 i A mi nije jedinicna matrica, no to nisam napisao jer sam napisao što je i A mi nije jedinicna matrica, no to nisam napisao jer sam napisao što je  , što je , što je 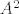 i što je i što je 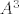 , pa nisam eksplicitno pisao što je jednako ili nije jednako, naravno osim , pa nisam eksplicitno pisao što je jednako ili nije jednako, naravno osim 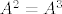 što mi je potrebno za rješenje. što mi je potrebno za rješenje. |
Ne znam da li pričamo o istoj stvari; samo iz toga što si napisao na papiru (drugo je što u glavi vidiš da nema drugih mogućnosti osim baš te koju si napisao) ne možeš zaključiti da je minimalni polinom  jer postoje matrice za koje vrijedi jer postoje matrice za koje vrijedi 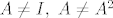 i i 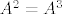 , ali minimalni polinom im nije , ali minimalni polinom im nije  . .
Da je 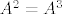 povlači povlači 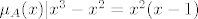 pa ili je pa ili je  minimalni polinom ili je A nilpotentna indeksa 2 ili je A=I. Budući da zadnja dva slučaja ne vrijede, tek onda slijedi da je minimalni polinom ili je A nilpotentna indeksa 2 ili je A=I. Budući da zadnja dva slučaja ne vrijede, tek onda slijedi da je 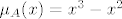
_________________
The Dude Abides
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
CrniVG
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (22:44:19)
Postovi: (23)16
|
|
| [Vrh] |
|
|










