| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:39 uto, 16. 11. 2010 Naslov: Postano: 18:39 uto, 16. 11. 2010 Naslov: |
    |
|
|
Dakako, a priori ne znamo postoji li neki [latex]n_0[/latex] nakon kojeg je niz padajući. Npr., za trivijalni niz [latex]a_n=n[/latex] očito ne postoji takav [latex]n_0[/latex]. No, mi smo ga tu eksplicitno našli, a samim njegovim pronalaženjem i pokazali da postoji.
Naprosto, pogledajmo čemu je ekvivalentno [latex]a_{n+1}\leq a_{n}[/latex]. To je upravo [latex]a\cdot a_n\leq (n+1)\cdot a_n[/latex] (pomnožili smo obje strane s [latex]n+1[/latex]). Sad, ako pretpostavimo da je [latex]a>0[/latex] (a ako je [latex]a[/latex] negativan, niz će stalno mijenjati predznak, pa takav [latex]n_0[/latex] nećemo moći pronaći jer će niz stalno padati, pa rasti, pa opet padati itd.), očito (formalno, indukcijom) vrijedi da je [latex]a_n>0[/latex], pa vidimo da je [latex]a\cdot a_n\leq (n+1)\cdot a_n\Leftrightarrow a\leq n+1[/latex], tj. [latex]n\geq a-1[/latex]. Sad, ja ne znam kako ste vi definirali "od kojeg nadalje je taj niz padajući" - tu ima možda neka sitna razlika s [latex]n+1[/latex] umjesto [latex]n[/latex] ili nešto, ja sam tu dobio da je zapravo već i [latex]n_0=\lceil a-1\rceil[/latex] sasvim u redu, ali to je ionako potpuno nebitno.
Dakle, mi smo pronašli takav [latex]n_0[/latex] - što je bitno, nismo prvo pretpostavili da on postoji, pa zatim ga koristeći to pronašli (jer bi tu bila neka logička greška sakrivena - mogao bi uistinu i ne postojati), nego smo ga odmah našli. Dakle, uistinu smo pokazali da ovaj [latex]n_0[/latex] zadovoljava tvrdnju.
Dakako, a priori ne znamo postoji li neki 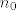 nakon kojeg je niz padajući. Npr., za trivijalni niz nakon kojeg je niz padajući. Npr., za trivijalni niz 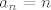 očito ne postoji takav očito ne postoji takav 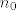 . No, mi smo ga tu eksplicitno našli, a samim njegovim pronalaženjem i pokazali da postoji. . No, mi smo ga tu eksplicitno našli, a samim njegovim pronalaženjem i pokazali da postoji.
Naprosto, pogledajmo čemu je ekvivalentno 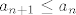 . To je upravo . To je upravo 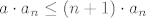 (pomnožili smo obje strane s (pomnožili smo obje strane s 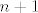 ). Sad, ako pretpostavimo da je ). Sad, ako pretpostavimo da je 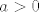 (a ako je (a ako je  negativan, niz će stalno mijenjati predznak, pa takav negativan, niz će stalno mijenjati predznak, pa takav 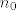 nećemo moći pronaći jer će niz stalno padati, pa rasti, pa opet padati itd.), očito (formalno, indukcijom) vrijedi da je nećemo moći pronaći jer će niz stalno padati, pa rasti, pa opet padati itd.), očito (formalno, indukcijom) vrijedi da je 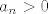 , pa vidimo da je , pa vidimo da je 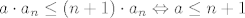 , tj. , tj. 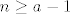 . Sad, ja ne znam kako ste vi definirali "od kojeg nadalje je taj niz padajući" - tu ima možda neka sitna razlika s . Sad, ja ne znam kako ste vi definirali "od kojeg nadalje je taj niz padajući" - tu ima možda neka sitna razlika s 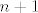 umjesto umjesto  ili nešto, ja sam tu dobio da je zapravo već i ili nešto, ja sam tu dobio da je zapravo već i 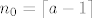 sasvim u redu, ali to je ionako potpuno nebitno. sasvim u redu, ali to je ionako potpuno nebitno.
Dakle, mi smo pronašli takav 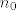 - što je bitno, nismo prvo pretpostavili da on postoji, pa zatim ga koristeći to pronašli (jer bi tu bila neka logička greška sakrivena - mogao bi uistinu i ne postojati), nego smo ga odmah našli. Dakle, uistinu smo pokazali da ovaj - što je bitno, nismo prvo pretpostavili da on postoji, pa zatim ga koristeći to pronašli (jer bi tu bila neka logička greška sakrivena - mogao bi uistinu i ne postojati), nego smo ga odmah našli. Dakle, uistinu smo pokazali da ovaj 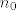 zadovoljava tvrdnju. zadovoljava tvrdnju.
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:02 uto, 16. 11. 2010 Naslov: Postano: 20:02 uto, 16. 11. 2010 Naslov: |
    |
|
|
[quote="kre5o"]još jedno pitance, ovaj put off topic, al pošto sam već tu..
Dakle kako dokazat da je [latex]<a,b>\sim[a,b]\sim\mathbb{R}[/latex][/quote]
Jedan način je da nađeš bijekciju među tim skupovima ili injekcije iz jednog u drugi i iz drugog u prvi.
Ili[spoiler]
Nije teško vidjeti da su svaka dva intervala oblika <a,b> i <c,d> istog kardinaliteta. Isto tako nije teško vidjeti da su svaka dva zatvorena intervala oblika [a,b] i [c,d] istog kardinaliteta. Dovoljno je promatrati odgovarajuću afinu funkciju na tim intervalima.
Zbog toga je dovoljno vidjeti da je npr. <0,1>~[0,1]. Jedna injekcija je f:<0,1>->[0,1], f(x)=x. Druga injekcija je g:[0,1]-><0,1>, g(x)=(x+1)/3.
Iz toga slijedi da je <a,b>~<0,1>~[0,1]~[a,b].
A da je <a,b>~R slijedi iz toga što je <a,b>~<-pi/2,pi/2>, a na intervalu <-pi/2,pi/2> postoji jedna elementarna bijektivna funkcija čija je kodomena R, a počinje sa t i rimuje se s angens.[/spoiler]
| kre5o (napisa): | još jedno pitance, ovaj put off topic, al pošto sam već tu..
Dakle kako dokazat da je 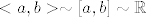 |
Jedan način je da nađeš bijekciju među tim skupovima ili injekcije iz jednog u drugi i iz drugog u prvi.
Ili | Spoiler [hidden; click to show]: |
Nije teško vidjeti da su svaka dva intervala oblika <a,b> i <c,d> istog kardinaliteta. Isto tako nije teško vidjeti da su svaka dva zatvorena intervala oblika [a,b] i [c,d] istog kardinaliteta. Dovoljno je promatrati odgovarajuću afinu funkciju na tim intervalima.
Zbog toga je dovoljno vidjeti da je npr. <0,1>~[0,1]. Jedna injekcija je f:<0,1>→[0,1], f(x)=x. Druga injekcija je g:[0,1]→<0,1>, g(x)=(x+1)/3.
Iz toga slijedi da je <a,b>~<0,1>~[0,1]~[a,b].
A da je <a,b>~R slijedi iz toga što je <a,b>~←pi/2,pi/2>, a na intervalu ←pi/2,pi/2> postoji jedna elementarna bijektivna funkcija čija je kodomena R, a počinje sa t i rimuje se s angens. |
_________________
The Dude Abides
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 20:15 uto, 16. 11. 2010 Naslov: Postano: 20:15 uto, 16. 11. 2010 Naslov: |
    |
|
|
ops, sori, preduhitren sam...
Pa za ovu prvu ekvipotenciju treba konstruirati dovoljno je konstruirati injekcije u oba smjera (po Cantor-Bernstein-Schröderovom teoremu).
Iz <a,b> u [a,b] se ocito mozemo posluziti identitetom, a lako se pokaze da je npr f(x)=(x+(a+b)/2)/2 injekcija s [a,b] u <a,b> (znamo da je linearna funkcija injektivna, samo je pitanje dal je slika [a,b] sadrzana u <a,b>)
Sad jos preostaje pokazati da su <a,b> i R ekvipotentni (iz toga ce slijediti ekvipotentnost s [a,b] jer se radi o relaciji ekvivalencije koja je, posebno, tranzitivna)
To mozemo pokazati kompozicijom sljedecih funkcija:
[latex]f_1(x)=\frac{\pi}{b-a}(x-a)-\frac{\pi}{2}[/latex]
[latex]f_2(x)=tg(x)[/latex]
f1 je bijekcija izmedju <a,b> i <-pi/2,pi/2>, a f2 bijekcija izmedju <-pi/2,pi/2> i R.
Iz ovog vidimo da je [latex]f_2\circ f_1[/latex] bijekcija s [latex]<a,b>[/latex] na [latex]\mathbb{R}
\Rightarrow <a,b> \sim \mathbb{R}[/latex]
ops, sori, preduhitren sam...
Pa za ovu prvu ekvipotenciju treba konstruirati dovoljno je konstruirati injekcije u oba smjera (po Cantor-Bernstein-Schröderovom teoremu).
Iz <a,b> u [a,b] se ocito mozemo posluziti identitetom, a lako se pokaze da je npr f(x)=(x+(a+b)/2)/2 injekcija s [a,b] u <a,b> (znamo da je linearna funkcija injektivna, samo je pitanje dal je slika [a,b] sadrzana u <a,b>)
Sad jos preostaje pokazati da su <a,b> i R ekvipotentni (iz toga ce slijediti ekvipotentnost s [a,b] jer se radi o relaciji ekvivalencije koja je, posebno, tranzitivna)
To mozemo pokazati kompozicijom sljedecih funkcija:
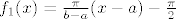
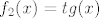
f1 je bijekcija izmedju <a,b> i ←pi/2,pi/2>, a f2 bijekcija izmedju ←pi/2,pi/2> i R.
Iz ovog vidimo da je 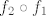 bijekcija s bijekcija s 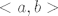 na na 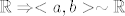
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
|







