| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
<gogo>
Forumaš(ica)


Pridružen/a: 09. 09. 2010. (09:09:31)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
<gogo>
Forumaš(ica)


Pridružen/a: 09. 09. 2010. (09:09:31)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
ninaaaaaaa
Forumaš(ica)

Pridružen/a: 12. 07. 2010. (16:54:36)
Postovi: (C)16
Spol: 
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 13:01 pon, 6. 12. 2010 Naslov: Postano: 13:01 pon, 6. 12. 2010 Naslov: |
    |
|
|
[quote="Buki"]Može pomoća sa prvim, molim vas. Ne znam ni otkud bi krenuo..[/quote]
"Dobro definirana" znači da zakon pridruživanja stvarno svakom elementu iz domene pridruži element iz kodomene (tj. da je dobivena permutacija neparna). Da bi to dokazao, koristi poznatu činjenicu [latex]\mathop{\mathrm{sign}} pq = \mathop{\mathrm{sign}} p \cdot \mathop{\mathrm{sign}} q[/latex].
A da bi dokazao da je funkcija bijekcija, dokaži da je injekcija (tj. da [latex]p_1q = p_2q[/latex] povlači [latex]p_1 = p_2[/latex], a tu će pomoći komponiranje s [latex]q^{-1}[/latex]) i da je surjekcija, tj. da se svaki element iz kodomene, nazovimo ga [latex]r[/latex], doista postiže i to kao [latex]\varphi(rq^{-1})[/latex].
| Buki (napisa): | | Može pomoća sa prvim, molim vas. Ne znam ni otkud bi krenuo.. |
"Dobro definirana" znači da zakon pridruživanja stvarno svakom elementu iz domene pridruži element iz kodomene (tj. da je dobivena permutacija neparna). Da bi to dokazao, koristi poznatu činjenicu 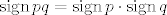 . .
A da bi dokazao da je funkcija bijekcija, dokaži da je injekcija (tj. da  povlači povlači 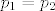 , a tu će pomoći komponiranje s , a tu će pomoći komponiranje s 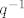 ) i da je surjekcija, tj. da se svaki element iz kodomene, nazovimo ga ) i da je surjekcija, tj. da se svaki element iz kodomene, nazovimo ga  , doista postiže i to kao , doista postiže i to kao 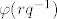 . .
|
|
| [Vrh] |
|
pman
Forumaš(ica)

Pridružen/a: 01. 11. 2009. (19:35:23)
Postovi: (3)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 21:08 pon, 6. 12. 2010 Naslov: Postano: 21:08 pon, 6. 12. 2010 Naslov: |
    |
|
|
Najprije, [latex]\mathop{\mathrm{sign}} pq = \mathop{\mathrm{sign}} p \cdot \mathop{\mathrm{sign}} q[/latex] iskoristiš tako da, ako je [latex]p[/latex] parna permutacija (pa je [latex]\mathop{\mathrm{sign}} p = 1[/latex]), a [latex]q[/latex] neparna permutacija (pa je [latex]\mathop{\mathrm{sign}} q = -1[/latex]), dobiješ da je [latex]\mathop{\mathrm{sign}} pq = -1[/latex] neparna permutacija.
Nadalje, zašto [latex]p_1q = p_2q[/latex] povlači [latex]p_1 = p_2[/latex] (injektivnost)? Zato jer [latex]p_1q = p_2q[/latex] možemo zdesna komponirati sa [latex]q^{-1}[/latex] i dobiti [latex](p_1q)q^{-1} = (p_2q)q^{-1}[/latex]. E sada, operacija komponiranja je asocijativna jer skup permutacija s operacijom komponiranja čini grupu, pa imamo [latex]p_1(qq^{-1}) = p_2(qq^{-1}) \quad \Rightarrow \quad p_1 = p_2[/latex].
Nadalje za [latex]r[/latex], neparnu permutaciju iz kodomene, pogledajmo [latex]\varphi(rq^{-1}) = (rq^{-1})q = r(q^{-1}q) = r[/latex], dakle imamo surjekciju jer se iz ovoga vidi da je [latex]r[/latex] funkcijska vrijednost (preskočio sam dokaz da je [latex]rq^{-1}[/latex] iz domene tj. parna permutacija, ali to ipak probaj sam).
Imam međutim primjedbu na gradivo Linearne algebre 1. Ove permutacije s kompozicijom čine [b]grupu[/b] i to je divna stvar koju sam u rješenju koristio, jer mi omogućava da razmišljam samo o svojstvima grupe (asocijativnost, inverzni element...) umjesto o samim permutacijama. Međutim grupe se u gradivu eventualno ovlaš spomenu i uopće ne obrade prije vektorskih prostora i matrica, a zapravo su to temeljnije i osnovnije stvari od vektorskih prostora. Zašto je to tako, zna li tko?
Najprije, 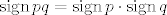 iskoristiš tako da, ako je iskoristiš tako da, ako je  parna permutacija (pa je parna permutacija (pa je 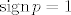 ), a ), a  neparna permutacija (pa je neparna permutacija (pa je 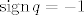 ), dobiješ da je ), dobiješ da je 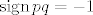 neparna permutacija. neparna permutacija.
Nadalje, zašto  povlači povlači 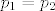 (injektivnost)? Zato jer (injektivnost)? Zato jer  možemo zdesna komponirati sa možemo zdesna komponirati sa 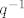 i dobiti i dobiti 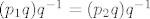 . E sada, operacija komponiranja je asocijativna jer skup permutacija s operacijom komponiranja čini grupu, pa imamo . E sada, operacija komponiranja je asocijativna jer skup permutacija s operacijom komponiranja čini grupu, pa imamo 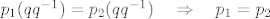 . .
Nadalje za  , neparnu permutaciju iz kodomene, pogledajmo , neparnu permutaciju iz kodomene, pogledajmo 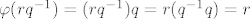 , dakle imamo surjekciju jer se iz ovoga vidi da je , dakle imamo surjekciju jer se iz ovoga vidi da je  funkcijska vrijednost (preskočio sam dokaz da je funkcijska vrijednost (preskočio sam dokaz da je 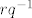 iz domene tj. parna permutacija, ali to ipak probaj sam). iz domene tj. parna permutacija, ali to ipak probaj sam).
Imam međutim primjedbu na gradivo Linearne algebre 1. Ove permutacije s kompozicijom čine grupu i to je divna stvar koju sam u rješenju koristio, jer mi omogućava da razmišljam samo o svojstvima grupe (asocijativnost, inverzni element...) umjesto o samim permutacijama. Međutim grupe se u gradivu eventualno ovlaš spomenu i uopće ne obrade prije vektorskih prostora i matrica, a zapravo su to temeljnije i osnovnije stvari od vektorskih prostora. Zašto je to tako, zna li tko?
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 6:10 čet, 9. 12. 2010 Naslov: Postano: 6:10 čet, 9. 12. 2010 Naslov: |
    |
|
|
Kad vec koristis cinjenicu da skup permutacija na n-clanom skupu cini grupu s operacijom komponiranja, zasto onda jednostavno ne bi iskoristio zatvorenost, dakle [latex]pq[/latex] je permutacija, dakle bijekcija ;)
Sto se tice gradiva linearne algebre, vrlo vjerojatno se tek ovlas spomenu jer ih se detaljno izucava na 2. godini na algebarskim strukturama, pa ni nema stvarne potrebe za tim.
Moj osobni stav je da je program vrlo elegantno izveden i, iako bi bilo lijepo da se obraduju grupe na 1. godini, ne bih volio da se mora zrtvovati ista od sadasnjeg programa linearne algebre. Eventualno gradivo elementarne geometrije u 2. semestru, ali tu je vec rijec o osobnim preferencijama :D
Mozda grupe i jesu temeljnije od vektorskih prostora, ali vektorski prostori su brucosima bitniji za znati jer igraju ogromnu ulogu na diferencijalnom racunu funkcija vise varijabli.
Kad vec koristis cinjenicu da skup permutacija na n-clanom skupu cini grupu s operacijom komponiranja, zasto onda jednostavno ne bi iskoristio zatvorenost, dakle 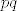 je permutacija, dakle bijekcija je permutacija, dakle bijekcija 
Sto se tice gradiva linearne algebre, vrlo vjerojatno se tek ovlas spomenu jer ih se detaljno izucava na 2. godini na algebarskim strukturama, pa ni nema stvarne potrebe za tim.
Moj osobni stav je da je program vrlo elegantno izveden i, iako bi bilo lijepo da se obraduju grupe na 1. godini, ne bih volio da se mora zrtvovati ista od sadasnjeg programa linearne algebre. Eventualno gradivo elementarne geometrije u 2. semestru, ali tu je vec rijec o osobnim preferencijama 
Mozda grupe i jesu temeljnije od vektorskih prostora, ali vektorski prostori su brucosima bitniji za znati jer igraju ogromnu ulogu na diferencijalnom racunu funkcija vise varijabli.
|
|
| [Vrh] |
|
|








