| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
diegobisbal
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (21:00:22)
Postovi: (21)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 16:47 čet, 2. 12. 2010 Naslov: Postano: 16:47 čet, 2. 12. 2010 Naslov: |
    |
|
|
Ovako bi se to dalo dokazati:
Definiramo nizove [latex]b_n=\prod_{k=0}^n(1+a_k)[/latex] i [latex]s_n=\sum_{k=0}^n a_k[/latex]
Sada treba pokazati [latex](b_n)[/latex] konvergira akko [latex]s_n[/latex] konvergira
1) neka [latex](s_n)[/latex] konvergira.
Koristimo nejednakost [latex]x+1 \leq e^x[/latex], iz koje dobivamo
[latex]
b_n \leq \prod_{k=0}^n e^{a_k} = e^{s_n}, \forall n\in \mathbb{N}[/latex]
Stavimo ovo na limes po n; kako je funkcija [latex]e^x[/latex] neprekidna i niz [latex](s_n)[/latex] konvergentan, dobivamo da je i niz [latex](e^{s_n})[/latex] konvergentan, iz cega mozemo zakljuciti da je niz [latex](b_n)[/latex] ogranicen. Kako je [latex](b_n)[/latex] ocito rastuc, iz ovoga imamo da je konvergentan.
2) Neka niz [latex](b_n)[/latex] konvergira.
Sad je dovoljno uociti [latex]b_n>s_n, \forall n\in \mathbb{N}[/latex] (to je ocito kad se razmnozi b_n, jer je sve pozitivno).
Kako je niz [latex](s_n)[/latex] rastuc, a majoriziran s nizom [latex](b_n)[/latex] koji je konvergentan, vrijedi isti zakljucak kao u 1), tj. [latex](s_n)[/latex] konvergira
Ovako bi se to dalo dokazati:
Definiramo nizove 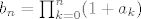 i i 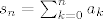
Sada treba pokazati 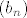 konvergira akko konvergira akko 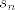 konvergira konvergira
1) neka 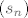 konvergira. konvergira.
Koristimo nejednakost 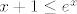 , iz koje dobivamo , iz koje dobivamo
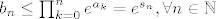
Stavimo ovo na limes po n; kako je funkcija 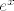 neprekidna i niz neprekidna i niz 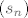 konvergentan, dobivamo da je i niz konvergentan, dobivamo da je i niz 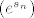 konvergentan, iz cega mozemo zakljuciti da je niz konvergentan, iz cega mozemo zakljuciti da je niz 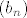 ogranicen. Kako je ogranicen. Kako je 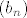 ocito rastuc, iz ovoga imamo da je konvergentan. ocito rastuc, iz ovoga imamo da je konvergentan.
2) Neka niz 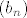 konvergira. konvergira.
Sad je dovoljno uociti 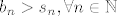 (to je ocito kad se razmnozi b_n, jer je sve pozitivno). (to je ocito kad se razmnozi b_n, jer je sve pozitivno).
Kako je niz 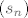 rastuc, a majoriziran s nizom rastuc, a majoriziran s nizom 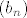 koji je konvergentan, vrijedi isti zakljucak kao u 1), tj. koji je konvergentan, vrijedi isti zakljucak kao u 1), tj. 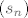 konvergira konvergira
|
|
| [Vrh] |
|
diegobisbal
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (21:00:22)
Postovi: (21)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
fireball
Forumaš(ica)


Pridružen/a: 07. 10. 2005. (18:49:17)
Postovi: (4AB)16
Spol: 
Lokacija: s rukom u vatri i nogom u grobu
|
|
| [Vrh] |
|
|









