| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Mignon
Forumaš(ica)


Pridružen/a: 12. 09. 2010. (14:05:45)
Postovi: (B6)16
Spol: 
Lokacija: 206
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 18:36 pet, 10. 12. 2010 Naslov: Postano: 18:36 pet, 10. 12. 2010 Naslov: |
    |
|
|
eh,da..imam i ja pitanje što se tiče tog zadatka. naime,kada razvijem f-ju u red,tj.kao:
x^3(x+x^3+x^5+...)(1+x^2+x^4+...)^2=x^4(1/1-x^2)^3 pa to sredim i izračunam koef. uz x^n(u b dijelu 28 ) ne dobijem isti koeficijent kao kada računam ovako:
x^3(x+x^3+x^5+...+x^19)(1+x^2+x^4+...+x^20)^2=x^4((1-x^19)/(1-x^2))((1-x^21)/(1-x^2))
je li to zato što kod prvog računjanja pretp.da mi prva i druga suma imaju jednako elemenata,a ustvari nemaju? neznam kako bi to precizno rekla..
i inače,kod takvih zadataka,kada je svejedno računam li na prvi ili drugi način? je li kada npr.u ovom zadatku treba izračunati koeficijen uz x na neki broj manji ili jednak 19?
eh,da..imam i ja pitanje što se tiče tog zadatka. naime,kada razvijem f-ju u red,tj.kao:
x^3(x+x^3+x^5+...)(1+x^2+x^4+...)^2=x^4(1/1-x^2)^3 pa to sredim i izračunam koef. uz x^n(u b dijelu 28 ) ne dobijem isti koeficijent kao kada računam ovako:
x^3(x+x^3+x^5+...+x^19)(1+x^2+x^4+...+x^20)^2=x^4((1-x^19)/(1-x^2))((1-x^21)/(1-x^2))
je li to zato što kod prvog računjanja pretp.da mi prva i druga suma imaju jednako elemenata,a ustvari nemaju? neznam kako bi to precizno rekla..
i inače,kod takvih zadataka,kada je svejedno računam li na prvi ili drugi način? je li kada npr.u ovom zadatku treba izračunati koeficijen uz x na neki broj manji ili jednak 19?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:01 sub, 11. 12. 2010 Naslov: Postano: 10:01 sub, 11. 12. 2010 Naslov: |
    |
|
|
[quote="pbakic"]Pa mislim da bi uvijek trebalo ispasti isto...
Jedino sto, u drugoj metodi rjesavanja (ovoj di ne gledas red nego konacnu sumu) imas napisano [latex]1+x^2+\dots+x^{18}=\frac{1-x^{19}}{1-x^2}[/latex], a trebalo bi biti [latex]\frac{1-x^{20}}{1-x^2}[/latex]
(i slicno za ovu sumu [latex]1+x^2+\dots+x^{20}[/latex])[/quote]
zašto? mislim,kak ide ta formula? je li zbog toga što zbrajamo potencije od [latex]x^2[/latex] ? zašto onda nije [latex]1-(x^2)^{n+1}[/latex] u brojniku?
i ne kužim zašto bi trebalo ispasti isto,npr.ako imamo [latex]{x^6,y^{20},z^{20},q^{28}}[/latex] i onaj gore primjer, broj načina da izaberemo 28 elemenata nije isti(zbog ovog [latex]q^{28}[/latex], jedan način nam je da izaberemo 3 x-eva,1 y, i 24 q-ova što gore nemamo ),a kada razvijemo u red,ispadne isti koeficijent jer su to isti redovi?
| pbakic (napisa): | Pa mislim da bi uvijek trebalo ispasti isto...
Jedino sto, u drugoj metodi rjesavanja (ovoj di ne gledas red nego konacnu sumu) imas napisano 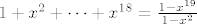 , a trebalo bi biti , a trebalo bi biti 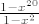
(i slicno za ovu sumu 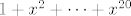 ) ) |
zašto? mislim,kak ide ta formula? je li zbog toga što zbrajamo potencije od 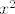 ? zašto onda nije ? zašto onda nije 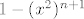 u brojniku? u brojniku?
i ne kužim zašto bi trebalo ispasti isto,npr.ako imamo 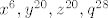 i onaj gore primjer, broj načina da izaberemo 28 elemenata nije isti(zbog ovog i onaj gore primjer, broj načina da izaberemo 28 elemenata nije isti(zbog ovog 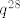 , jedan način nam je da izaberemo 3 x-eva,1 y, i 24 q-ova što gore nemamo ),a kada razvijemo u red,ispadne isti koeficijent jer su to isti redovi? , jedan način nam je da izaberemo 3 x-eva,1 y, i 24 q-ova što gore nemamo ),a kada razvijemo u red,ispadne isti koeficijent jer su to isti redovi?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 16:00 sub, 11. 12. 2010 Naslov: Postano: 16:00 sub, 11. 12. 2010 Naslov: |
    |
|
|
Sori, malo sam bio u zurbi pa nisam bas najbolje razmislio o tom sta pisem :)
Uglavnom, kad imamo ograniceni (tj konacan) multiskup, onda ne mozemo zapisivat ove zagrade kao redove - ako ga napisemo do prevelikog clana, onda brojimo i neke nezeljene kombinacije.
Npr, kad imamo x^3(x+x^3+x^5+...)(1+x^2+x^4+...)^2 onda ocito 28 clanova mozemo izbrojat kao 3 iz prvog clana, 1 iz drugog, 24 iz treceg i 0 iz cetvrtog (a to ocito nije dobro jer smo premasili 20 u trecem)
S druge strane, kad je multiskup beskonacan, npr [latex]{x^{\infty},y^{\infty}}[/latex], onda je svejedno dal zapisemo sve zagrade kao redove (beskonacne) ili konacne, do onog clana koji nas zanima (npr, ako zelimo brojati nkn mozemo dobiti 28, onda sume zapisemo do x^28, jer s ovim vecima i tako ne mozemo postici 28 ); to je zato sto mnozenje redova odgovara mnozenju (konacnih) polinoma
E a za ove sume geometrijskih nizova, imamo, na primjer [latex]1+x^2+x^4+\dots+x^{18}[/latex]. Sad, mozda je ljepse gledat uz supst. [latex]y=x^2[/latex] tako da imamo sumu [latex]1+y+\dots+y^9=\frac{1-y^{10}}{1-y}=\frac{1-x^{20}}{1-x^2}[/latex]
Sori, malo sam bio u zurbi pa nisam bas najbolje razmislio o tom sta pisem 
Uglavnom, kad imamo ograniceni (tj konacan) multiskup, onda ne mozemo zapisivat ove zagrade kao redove - ako ga napisemo do prevelikog clana, onda brojimo i neke nezeljene kombinacije.
Npr, kad imamo x^3(x+x^3+x^5+...)(1+x^2+x^4+...)^2 onda ocito 28 clanova mozemo izbrojat kao 3 iz prvog clana, 1 iz drugog, 24 iz treceg i 0 iz cetvrtog (a to ocito nije dobro jer smo premasili 20 u trecem)
S druge strane, kad je multiskup beskonacan, npr 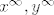 , onda je svejedno dal zapisemo sve zagrade kao redove (beskonacne) ili konacne, do onog clana koji nas zanima (npr, ako zelimo brojati nkn mozemo dobiti 28, onda sume zapisemo do x^28, jer s ovim vecima i tako ne mozemo postici 28 ); to je zato sto mnozenje redova odgovara mnozenju (konacnih) polinoma , onda je svejedno dal zapisemo sve zagrade kao redove (beskonacne) ili konacne, do onog clana koji nas zanima (npr, ako zelimo brojati nkn mozemo dobiti 28, onda sume zapisemo do x^28, jer s ovim vecima i tako ne mozemo postici 28 ); to je zato sto mnozenje redova odgovara mnozenju (konacnih) polinoma
E a za ove sume geometrijskih nizova, imamo, na primjer 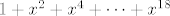 . Sad, mozda je ljepse gledat uz supst. . Sad, mozda je ljepse gledat uz supst. 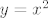 tako da imamo sumu tako da imamo sumu 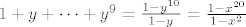
|
|
| [Vrh] |
|
|










